“文心CV大模型” - VIMER-UFO论文报告

VIMER-UFO
UFO（Unified Feature Optimization）（统一特征优化）
我以为是模仿外星人神经，做的模型呢

目的是实现：

1. 功能更强大、更通用的视觉模型模型
2. 灵活、可伸缩的弹性部署方案

1.论文背景：

1.以前，主流的视觉模型生产流程通常采用单任务的“从零开始训练”方案，每个任务都是独立的，无法相互借鉴。由于单任务数据不足，会导致偏置问题，实际效果过于依赖任务数据分布，场景泛化效果不佳。而近年来，大数据预训练技术蓬勃发展，通过使用大量数据学习更多的通用知识，然后将这些知识迁移到下游任务中。这本质上是不同任务之间相互借鉴各自学到的知识。基于海量数据获得的预训练模型具有较好的知识完备性，在下游任务中，即使只有少量数据，通过微调依然可以获得较好的效果。但是，基于预训练+下游任务微调的模型生产流程需要针对每个任务分别训练模型，这会耗费大量的研发资源。

2.由于算力和存储的限制，大型模型无法直接部署在边缘设备上。为了在边缘设备或端设备上部署云端设备开发的模型，通常需要进行模型压缩或重新设计，但预训练大模型本身的压缩也需要消耗大量资源。
此外，不同任务对模型的功能和性能要求也不同。例如，人脸识别门禁系统只需要具备人脸识别功能，而智慧社区的管控系统则需要同时具备人脸识别和人体分析的能力，部分场景还需要同时具备车型识别及车牌识别能力。即使是同样的人脸识别任务，门禁系统和金融支付系统对模型的精度和性能要求也不同。为了适应这些任务，需要开发多个单任务模型，并适配不同的硬件平台。因此，AI模型开发的工作量显著增加。

针对这样的背景下的问题，百度提出的VIMER-UFO模型解决方案如下：

百度提出的 VIMER-UFO All in One 多任务训练方案，通过使用多个任务的数据训练一个功能强大的通用模型，可被直接应用于处理多个任务。

并且VIMER-UFO 2.0 基于 Vision Transformer 结构设计了多任务多路径超网络。与谷歌 Switch Transformer 以图片为粒度选择路径不同，VIMER-UFO 2.0 以任务为粒度进行路径选择，这样当超网络训练好以后，可以根据不同任务独立抽取对应的子网络进行部署，而不用部署整个大模型。VIMER-UFO 2.0 的超网中不同的路径除了可以选择不同 FFN 单元，Attention 模块和 FFN 模块内部也支持弹性伸缩，实现网络的搜索空间扩展，为硬件部署提供更多可选的子网络，并提升精度。

引入超网络的概念，超网络由众多稀疏的子网络构成，每个子网络是超网络中的一条路径，将不同参数量、不同任务功能和不同精度的模型训练过程变为训练一个超网络模型。训练完成的 VIMER-UFO One for All 超网络大模型即可针对不同的任务和设备低成本生成相应的可即插即用的小模型，实现 One for All Tasks 和 One for All Chips 的能力。

下面章节将讲述VIMER-UFO方法的相关工作和方法论

UFO包含三个步骤即：

• 多任务特征优化
• 训练一个多任务超级网络
• 提取一个专门的子网络用于下游任务部署

2.多任务特征优化

UFO多任务特征优化核心思想是通过优化特征，实现不同任务之间参数的共享和转移。

具体来说，UFO方法采用特征选择和特征融合两个步骤来优化基础模型提取特征的能力。

• 特征选择：UFO方法使用自适应门控机制来动态选择每个任务的特征子集。
• 特征融合：UFO方法将任务特定特征和通用特征结合起来，通过全局特征转移来提高模型的泛化能力。

2.1 特征选择

适应门控机制（Adaptive Gate Mechanism，简称AGM）是一种动态选择特征子集的方法，可以用于实现深度学习模型中不同任务之间的参数共享和转移，同时也可以用于特征选择。其原理基于门控机制，可以通过一个可学习的门控参数来控制特征子集的选择。

具体而言，AGM的原理是在模型中插入一个门控机制，用来动态地选择当前任务需要的特征子集。这个门控机制通过一个可学习的门控参数来控制每个特征的权重，从而选择特定的特征子集。

在训练过程中，AGM可以通过反向传播算法自适应地学习门控参数，以便更好地选择特征子集。具体而言，AGM的公式如下所示：

$$y=\sigma ({\text{W}}_{f}x+b_f)\odot ({\text{W}}_{g}x+b_g)$$
其中，$x$表示输入特征向量，$y$表示输出特征向量，$\sigma$表示Sigmoid函数，$\odot$表示按元素乘法，${\text{W}}_f$和$b_f$表示门控机制的参数，${\text{W}}_g$和$b_g$表示特征权重的参数。门控参数${\text{W}}_f$和$b_f$控制每个特征的门控状态，门控状态为1表示该特征被选中，为0表示该特征被剔除；特征权重参数${\text{W}}_g$和$b_g$用来控制每个特征的权重大小，从而影响特征的重要性。具体来说，门控参数${\text{W}}_f$和$b_f$的计算方式如下：

$$W_f={\text{w}}_f{\text{w}}_f^T,b_f=-\lambda {\text{w}}_f$$

其中，${\text{w}}_f$是一个可学习的门控向量，$\lambda$是一个超参数，用来控制门控状态的稀疏性。当门控状态为1时，对应的特征被选择；当门控状态为0时，对应的特征被剔除。特征权重参数$W_g$和$b_g$的计算方式如下：

$${\text{W}}_g={\text{w}}_g{\text{w}}_g^T,b_g=0$$
其中，${\text{w}}_g$是一个可学习的特征权重向量，用来控制每个特征的权重大小。通过这种适应门控机制，可以动态地选择特定的特征子集，从而实现不同任务之间的参数共享和转移，同时也可以用于特征选择。

2.2 特征融合

特征融合是一种将多个任务的特征表示映射到一个共享的特征空间中的方法，可以用于实现深度学习模型中不同任务之间的参数共享和转移。其中，基于线性映射的方法是一种常用的特征融合方法，它通过最小化多个任务之间的距离来学习特征映射。

具体而言，基于线性映射的方法将每个任务的特征表示映射到一个共享的特征空间中，使得不同任务的特征表示可以进行比较和融合。在这个特征空间中，每个任务的特征表示可以看作是一个向量，多个任务的特征表示可以组成一个矩阵。为了实现特征融合，需要学习一个线性映射矩阵，将每个任务的特征表示映射到共享的特征空间中。

线性映射的方法通常采用最小化多个任务之间的距离来学习映射矩阵。具体而言，可以定义一个距离函数，用来度量不同任务之间的相似性或距离。然后，通过最小化多个任务之间的距离来学习映射矩阵，使得多个任务的特征表示在共享的特征空间中具有相似的表示。

具体来说，假设有$n$个任务，每个任务的特征表示为$X_i\in {\mathbb{R}}^{d_i\times m}$，其中$d_i$表示第$i$个任务的特征维度，$m$表示样本数。将$n$个任务的特征表示合并为一个矩阵$X=[X_1,X_2,...,X_n]$，则特征融合的目标是学习一个映射矩阵$W\in {\mathbb{R}}^{k\times d}$，将$X$映射到共享的特征空间$Z\in {\mathbb{R}}^{k\times m}$，$k$表示共享的特征维度，$d={\sum }_{i=1}^n{d}_i$表示所有任务的特征维度之和。

$X$矩阵可以如下图所示，

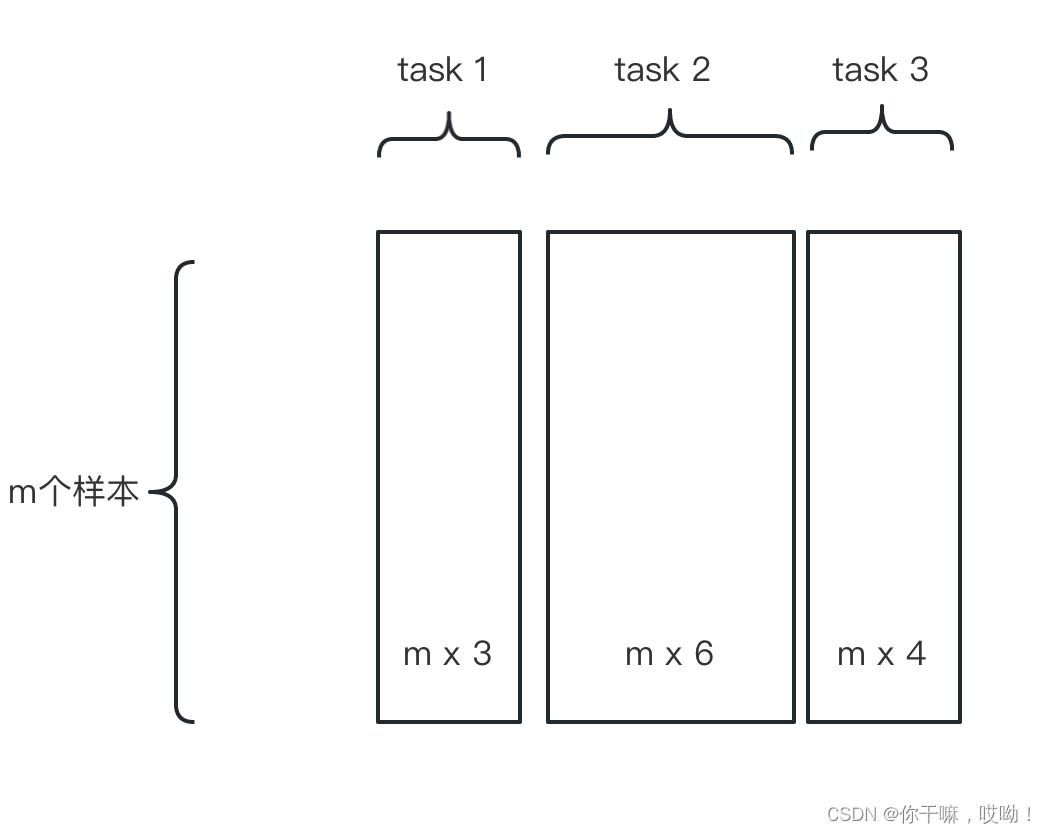
线性映射的公式为：

$$Z=WX$$
其中，$X$表示原始的特征矩阵，$W$表示学习到的映射矩阵，$Z$表示映射后的特征矩阵。

如何求解W映射矩阵

线性映射的方法可以通过最小化多个任务之间的距离来学习映射矩阵$W$。具体而言，可以定义一个距离函数，用来度量不同任务之间的相似性或距离。常用的距离函数包括欧氏距离、曼哈顿距离、余弦距离等。

假设使用欧氏距离作为距离函数，则任务$i$和任务$j$之间的距离可以定义为：
$$D_{i,j}=||W{X}_i-W{X}_j|{|}_F^2$$

其中，$\Vert \cdot {\Vert }_F$表示矩阵的Frobenius范数。

则特征融合的目标是最小化多个任务之间的距离，即最小化距离矩阵$D$，可以表示为以下优化问题
$$mi{n}_w\sum _{i,j}{w}_{i,j}{D}_{i,j}$$

其中，$w_{i,j}$表示任务$i$和任务$j$之间的权重，可以根据任务之间的关系、样本分布等信息来确定。$w_{i,j}$可以看作是一个对称矩阵，满足$w_{i,j}=w_{j,i}$，并且对角线元素为$w_{i,i}=0$，表示任务$i$与自身的距离为0。上述优化问题可以通过梯度下降等优化方法来求解，从而得到最优的映射矩阵$W$。

多任务特征优化的方法都旨在通过调整模型的训练策略，从而最小化所有任务的损失函数，以提高模型的性能。

2.3 模型架构

下面将介绍模型结构方面的内容，文中介绍了软参数共享和硬参数共享两种方式。

• 软参数共享：允许每个任务有不同的模型和参数，但通过正则化器或NAS搜索结构来保证每个模型可以访问其他模型内部的信息。
• 硬参数共享：使用共享的主干参数和任务特定的模块。

除了这两种方式外，还提到了一种结合了共享和任务特定模块的架构，以及一种从超网中提取子网的方法，这些方法都旨在优化多任务学习的性能。然而，所有这些方法都考虑通过鼓励单个任务之间的信息交互或引入任务特定模块来添加组件，但忽略了减少模块的思想。

相比之下，百度的方法通过从超网中减少不兼容的权重并保留互补的权重来提取子网。与 Task-MOE 类似，百度的方法也采用任务级路由器选择特定的 FFN。然而，百度的方法为每个任务提取最合适的自注意子权重，而 Task-MOE 则在所有任务中共享完整的自注意权重。

超网

深度学习中的超网络方法是指在一个大规模的网络中，通过对子网络的超参数进行搜索和优化，从而得到一个适合特定任务的小型网络。与传统的网络压缩方法相比，超网络方法不需要手动指定网络结构，而是通过自动搜索的方式得到最优的网络结构，具有更高的效率和准确率。

超网络方法的核心是超参数优化。具体来说，超网络由一个大型网络和一个子网络组成。大型网络包括所有可能的子网络，而子网络则由超参数控制。
超参数是影响模型训练和性能的重要参数，例如学习率、卷积核大小、神经元个数等。通过对超参数进行优化，超网络方法可以得到一个适合特定任务的小型网络。超参数优化的方法主要有两种：基于演化算法的方法和基于梯度下降的方法。其中，基于演化算法的方法通常使用遗传算法或粒子群算法等进化算法进行搜索，而基于梯度下降的方法通常使用反向传播算法进行搜索。在实践中，超网络方法通常会结合这两种方法进行优化。

超网络方法可以应用于许多深度学习任务，如图像分类、目标检测、语义分割等。下面是一个基于梯度下降的超网络优化的示例，其中使用了基于自适应矩阵的梯度下降算法（Adam）：

假设子网络的输出为 $y(x;\theta )$，其中 $x$ 表示输入，$\theta$ 表示超参数。目标是最小化损失函数 $L(y(x;\theta ),t)$，其中 $t$ 表示目标值。使用 Adam 算法更新超参数 $\theta$：

$${\theta }_{t+1}={\theta }_t-\frac{\eta }{\sqrt{{\hat{v}}_t}+ϵ}{\hat{m}}_t$$

其中，$\eta$ 是学习率，$ϵ$ 是一个非常小的数，${\hat{m}}_t$ 和 ${\hat{v}}_t$ 分别表示梯度的一阶矩估计和二阶矩估计：

$${\hat{m}}_t=\frac{m_t}{1-{\beta }_1^t},{\hat{v}}_t=\frac{v_t}{1-{\beta }_2^t}$$

其中，$m_t$ 和 $v_t$ 分别表示梯度的一阶矩和二阶矩，${\beta }_1$ 和 ${\beta }_2$ 是超参数，用于控制一阶矩和二阶矩的权重。通过反向传播算法计算梯度，即：
$$g_t=\frac{\partial L(y(x;{\theta }_t),t}{\partial {\theta }_t}$$

然后，计算梯度的一阶矩和二阶矩：然后，计算梯度的一阶矩和二阶矩：
$$m_t={\beta }_1{m}_{t-1}+(1-{\beta }_1)g_t,v_t={\beta }_2{v}_{t-1}+(1-{\beta }_2)g_t^2$$

最后，使用上述公式更新超参数 $\theta$。 需要注意的是，超网络方法需要消耗大量的计算资源和时间。因此，通常需要使用分布式训练或者GPU等高性能计算设备来加速训练过程。另外，超网络方法的搜索空间非常大，很容易陷入局部最优解，因此需要使用一些特殊的技术来避免这种情况的发生，例如剪枝、正则化等。 总之，超网络方法是一种非常有前景的深度学习技术，可以帮助我们快速高效地设计出适合特定任务的神经网络，从而提高模型的性能和效率。

3.训练一个多任务超级网络

在这种新的训练和部署范式下，UFO旨在保持多任务预训练的互惠益处，消除不同任务之间的冲突。为此，我们采用神经架构搜索（NAS）方法从超级网络中搜索子网络。

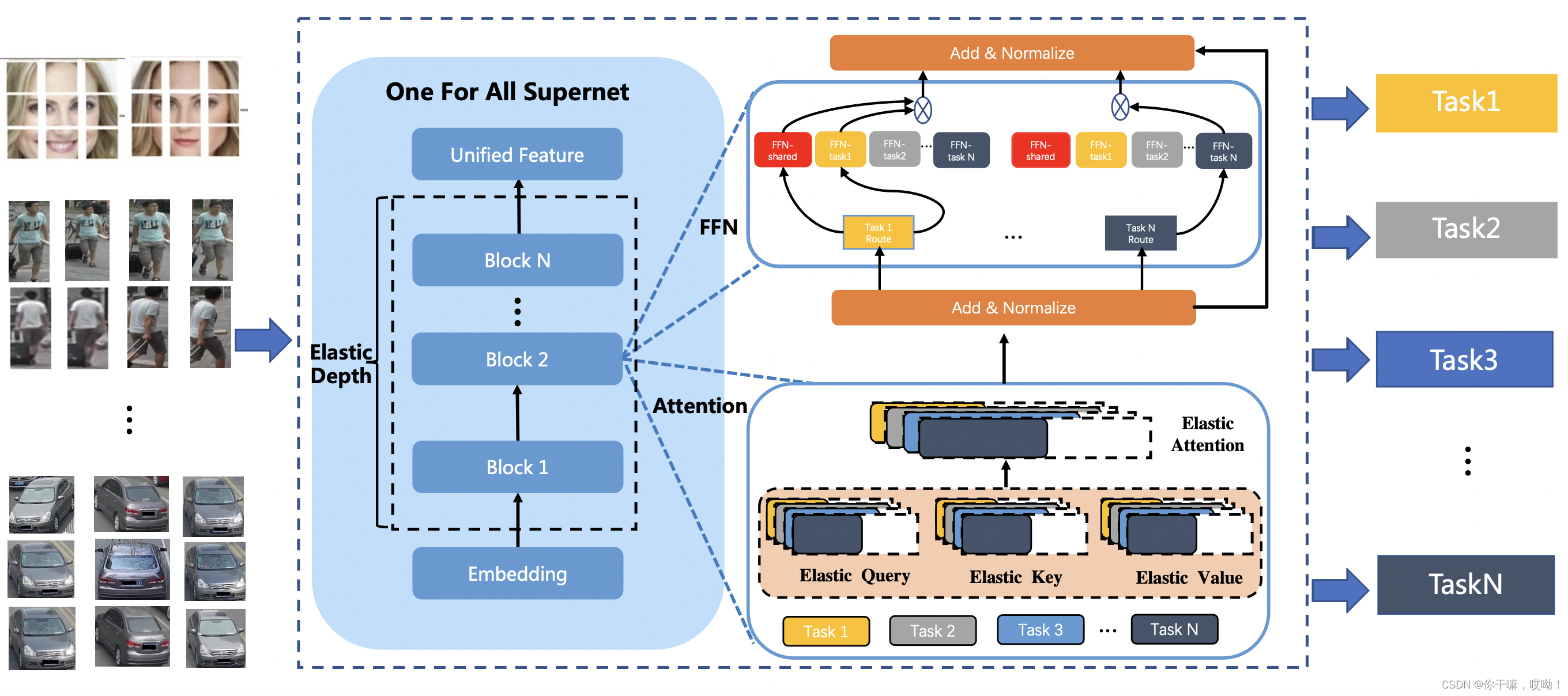
3.1 UFO超级网络的架构和搜索空间

如上图1所示，我们基于视觉变换器（ViT）构建UFO超级网络。
一个block由FFN和Attention共同组成

由于子网络在部署时从超级网络中选择部分模块并继承相应的参数，因此超级网络提供大的搜索空间以搜索和提取子网络是非常重要的。之前基于变压器的NAS通常提供三个搜索方向，即弹性深度、弹性注意力头和前馈网络（FFN）的弹性扩张比率。

除了这些常用的搜索方向外，我们引入了一种新的搜索方向，即灵活的FFN路径。

换句话说，UFO将三个常用的搜索方向和一个新的方向相结合，从而提供了大的搜索空间。因此，子网络可以减少FFN路径、FFN权重、注意力权重甚至视觉变换器的整个子块。我们将详细说明这些搜索方向。

假设模型架构空间由一组架构组成（就是不同模型块组合成的）

假设架构为A，A是由一组元素构成的集合，每个元素由多个组件组成。其中，D={0,1}是用来表示是否丢弃整个层的选择集合。整个搜索空间A可以用如下方式表示：
$$A=[[h1,m1,g1,d1],[h2,m2,g2,d2],\cdot \cdot \cdot ,[hl,ml,gl,dl]],hi\in H,mi\in M,gi\subseteq G,di\in D,\forall i\in 1,2,\cdot \cdot \cdot ,l$$

其中，l代表模型的层数。G确定不同任务的前馈神经网络路径，H和M决定不同子网络的模型大小，D控制子网络的深度以进一步减小模型的大小。

当给定任务t的输入$x_i^t$时，模型将从A中随机抽样一个架构a，然后依次计算该架构的连续块。

$${\hat{x}}_i^t=d_l\ast MHSA(LN(x_i^t),h_l)+x_t^i$$
$$x_{i+1}^t=d_l\ast FFNs(LN({\hat{x}}_i^t),m_i,g_i^t)+{\hat{x}}_t^i$$

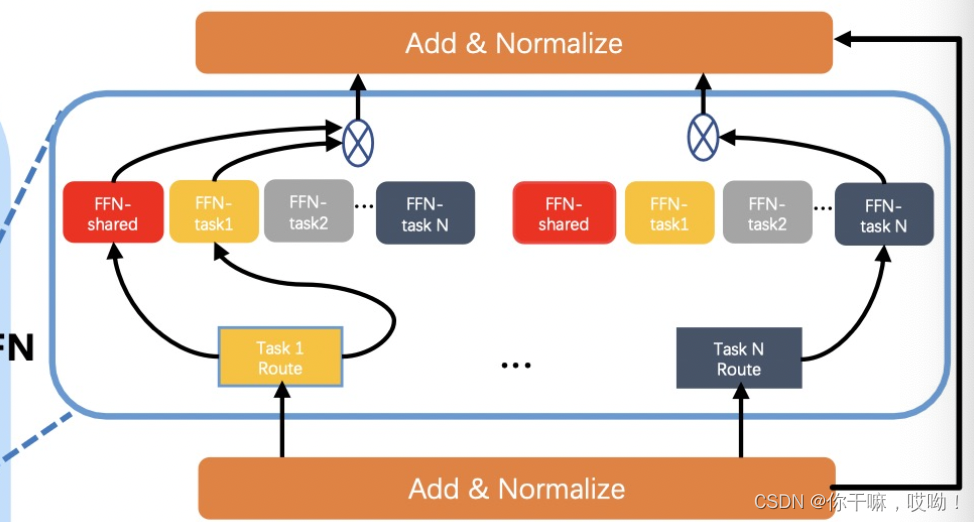
3.2 UFO超网训练

当训练多任务的UFO超网时，需要进行子网络采样和数据采样。其中，子网络采样涉及到采样一组参数 $(m_l,h_l,d_l,g_l)$，用于确定任务 $t$ 的输入 $x_i^t$ 的权重与超网的权重共享的部分。

在UFO中，FFN路径可以减轻共享注意力的竞争，因此可以端到端地进行训练。但是，如果我们直接从 $A$ 中采样与 $g_l$ 相关的子网络，由于 FFN 路径的总数很大，即 $|T|\times (2^{|G|}-1{)}^l$，超网很难收敛。因此，为每个任务的路径门设置了约束条件，其中每个任务每个层只有三种选择，即共享 FFN、任务特定 FFN 或二者兼有。

具体来说，我们使用可学习门权重上的Gumbel-Softmax采样概率分布来采样任务t的路径门。因此，FFN的输出（我们忽略了层/块idx i）可以定义为：

$$FNNs(\cdot )=p^t[0]FF{N}_{shared}(\cdot )+p^t[1]FF{N}_{task-specific}^t(\cdot )$$

训练后，学习到的门权重决定了门的单一选择
通过argmax或同时选择两个门。通过这种方式，FFN路径的总数为
从$|T|\times (2^{|G|}-1{)}^l$减少到$|T|\times |3{|}^l$。

数据采样

对于数据采样，文章提到了五种现有的方法，其中累积梯度策略是最有前途的。文章提出了一种类似但不同的策略，称为异构批次类型。该策略从所有任务的数据中采样一些数据，形成一个小批次，其权重大致与任务数据集的大小成比例。然后，这些小批次被连接成一个批次数据，输入到骨干网络中。接下来，获得的特征被分离并输入到每个任务特定的头网络中，每个头网络负责输出一个任务的结果。最后，计算|T|个任务的损失，对共享变换骨干网络进行求和，完成一次反向传播，并获得用于更新共享参数的梯度。

3.3 提取子网络

在提取子网络方面，文章提出了一种寻找最优体系结构的方法，以便在flops和参数约束条件下，最大化平均性能。除了针对目标任务的极端性能，我们还关注其他任务的广义性能。因此，文章提出了一个综合性能度量$av{g}_{f(t,a)}$，用于衡量所有任务上的体系结构性能。

设$f_t(a)$是架构a在任务t上的性能，$\forall t\in T，\forall a\in A$。
然后， 除了目标任务的极端性能外，我们还关心
其他任务的一般性能。因此，设avg_f(t,a)为综合
体系结构在所有任务上的性能，其中：

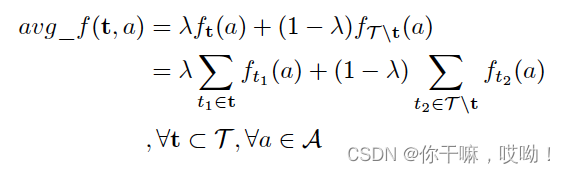
论文结果

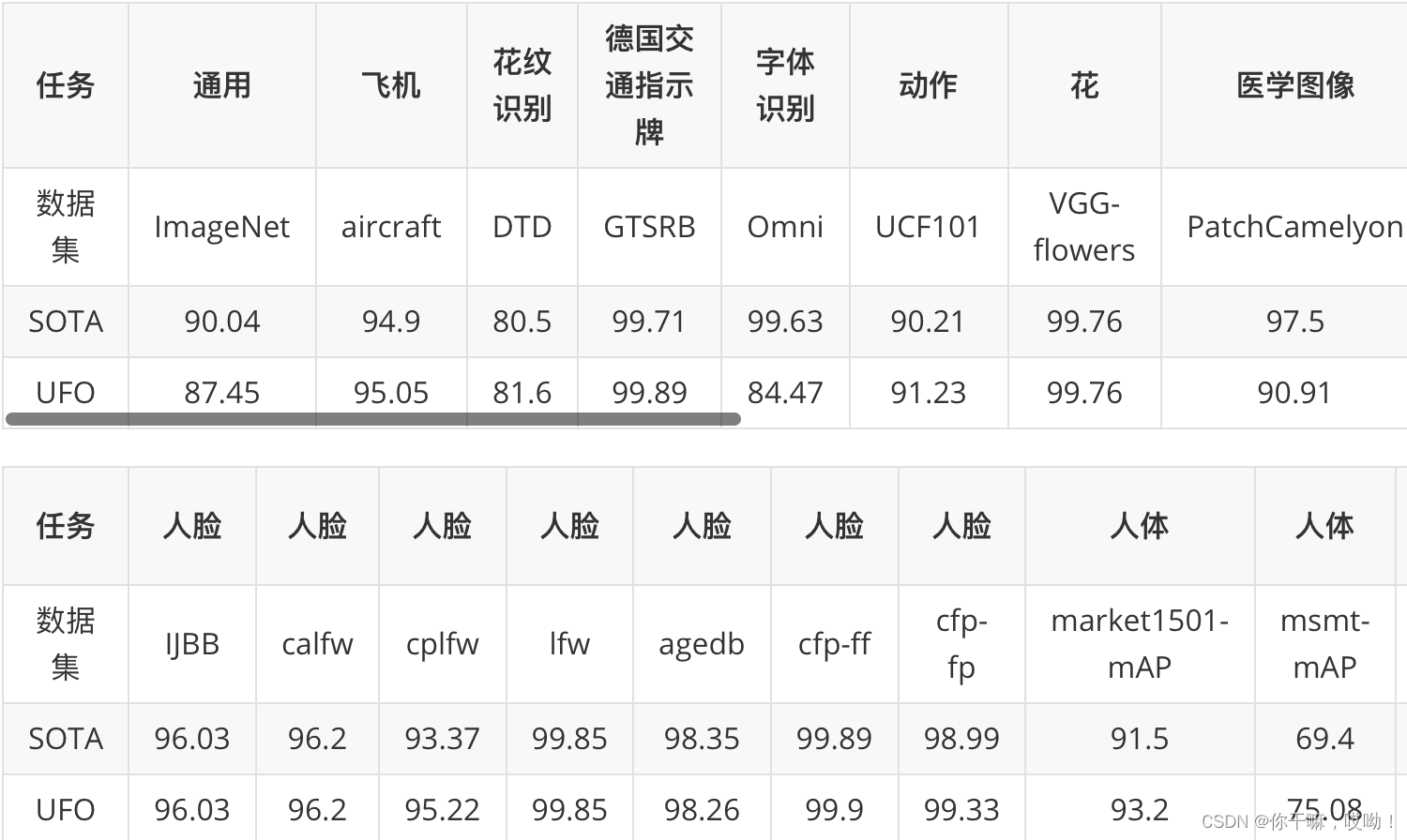
VIMER-UFO 2.0 单个模型一套参数，在不进行下游finetuning的情况下，在 28 个主流的 CV 公开数据集上取得了 SOTA 的结果

文章好在哪里：

UFO方法提出了一种新的多任务学习方法，将特征优化和多任务学习结合起来，并且在实现高精度和高效率方面都取得了显著的成功。与现有的多任务学习方法相比，UFO方法具有更少的参数和更快的推理速度，同时保持了高准确性。此外，UFO还可以解释其特征选择的原因。

个人想法：

UFO方法是一种非常有用和有前途的多任务学习方法，能够帮助研究人员在解决多个任务时节省时间和资源。此外，UFO还可以提高多任务学习的可解释性，使人们更好地理解特征子集的选择过程。然而，需要注意的是，UFO方法虽然表现良好，但也存在一些限制和不足，如无法处理不同任务之间的耦合性。因此，需要进一步研究和改进。