DBSCAN聚类算法——基于密度的聚类方式（理论+图解+python代码）_基于密度的聚类算法

一、DBSCAN聚类概述

基于密度的方法的特点是不依赖于距离，而是依赖于密度，从而克服基于距离的算法只能发现“球形”聚簇的缺点。
DBSCAN的核心思想是从某个核心点出发，不断向密度可达的区域扩张，从而得到一个包含核心点和边界点的最大化区域，区域中任意两点密度相连。

1、伪代码

算法： DBSCAN
输入： E — 半径
MinPts — 给定点在 E 领域内成为核心对象的最小领域点数
D — 集合
输出：目标类簇集合
方法： repeat

1. 判断输入点是否为核心对象
2. 找出核心对象的 E 领域中的所有直接密度可达点

util 所有输入点都判断完毕
repeat
针对所有核心对象的 E 领域所有直接密度可达点找到最大密度相连对象集合，
中间涉及到一些密度可达对象的合并。
Util 所有核心对象的 E 领域都遍历完毕

密度：空间中任意一点的密度是以该点为圆心，以EPS为半径的圆区域内包含的点数目
边界点：空间中某一点的密度，如果小于某一点给定的阈值minpts,则称为边界点
噪声点：不属于核心点，也不属于边界点的点，也就是密度为1的点

2、优点：

• 这类算法能克服基于距离的算法只能发现“类圆形”(凸)的聚类的缺点
• 可发现任意形状的聚类，且对噪声数据不敏感。
• 不需要指定类的数目cluster
• 算法中只有两个参数，扫描半径 (eps)和最小包含点数(min_samples)

3、缺点：

• 1、计算复杂度，不进行任何优化时，算法的时间复杂度是O(N^{2})，通常可利用R-tree，k-d tree, ball
  tree索引来加速计算，将算法的时间复杂度降为O(Nlog(N))。
• 2、受eps影响较大。在类中的数据分布密度不均匀时，eps较小时，密度小的cluster会被划分成多个性质相似的cluster；eps较大时，会使得距离较近且密度较大的cluster被合并成一个cluster。在高维数据时，因为维数灾难问题，eps的选取比较困难。
• 3、依赖距离公式的选取，由于维度灾害，距离的度量标准不重要
• 4、不适合数据集集中密度差异很大的，因为eps和metric选取很困难

4、与其他聚类算法比较

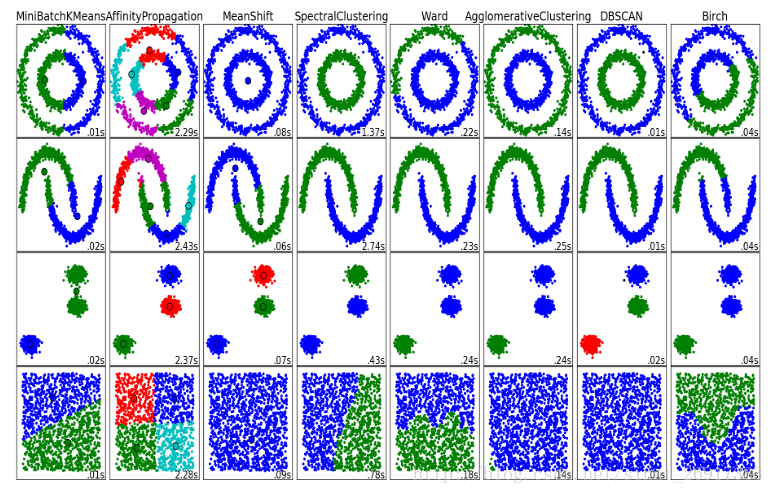
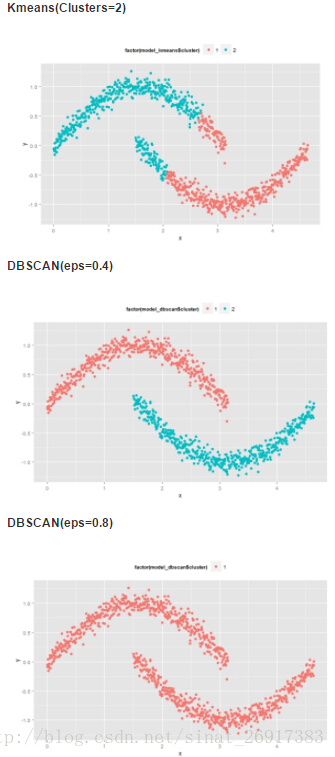
来看两张图：

DBSCAN可以较快、较有效的聚类出来

eps的取值对聚类效果的影响很大。
.

---

二、sklearn中的DBSCAN聚类算法

1、主要函数介绍：

DBSCAN(eps=0.5, min_samples=5, metric='euclidean', algorithm='auto', leaf_size=30, p=None, n_jobs=1)

 
 

 
 
1

最重要的两个参数：

eps:两个样本之间的最大距离，即扫描半径
min_samples ：作为核心点的话邻域(即以其为圆心，eps为半径的圆，含圆上的点)中的最小样本数(包括点本身)。
其他参数：
metric ：度量方式，默认为欧式距离，还有metric=‘precomputed’（稀疏半径邻域图）
algorithm：近邻算法求解方式，有四种：‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’
leaf_size：叶的大小，在使用BallTree or cKDTree近邻算法时候会需要这个参数
n_jobs ：使用CPU格式，-1代表全开

其他主要属性：

core_sample_indices_:核心样本指数。（此参数在代码中有详细的解释）
labels_:数据集中每个点的集合标签给,噪声点标签为-1。
components_ ：核心样本的副本

运行式子：

model = sklearn.cluster.DBSCAN(eps_领域大小圆半径,min_samples_领域内，点的个数的阈值)
model.fit(data) 训练模型
model.fit_predict(data) 模型的预测方法
.

2、DBSCAN自编代码

来源：【挖掘模型】：Python-DBSCAN算法

import numpy
import pandas
import matplotlib.pyplot as plt

#导入数据
data = pandas.read_csv("F:\\python 数据挖掘分析实战\\Data\\data (7).csv")

plt.scatter(
    data['x'], 
    data['y']
)

eps = 0.2;
MinPts = 5;

from sklearn.metrics.pairwise import euclidean_distances

ptses = []
dist = euclidean_distances(data)
for row in dist:
    #密度,空间中任意一点的密度是以该点为圆心、以 Eps 为半径的圆区域内包含的点数
    density = numpy.sum(row<eps)
    pts = 0;
    if density>MinPts:
        #核心点（Core Points）
        #空间中某一点的密度，如果大于某一给定阈值MinPts，则称该为核心点
        pts = 1
    elif density>1 :
        #边界点（Border Points）
        #空间中某一点的密度，如果小于某一给定阈值MinPts，则称该为边界点
        pts = 2
    else:
        #噪声点（Noise Points）
        #数据集中不属于核心点，也不属于边界点的点，也就是密度值为1的点
        pts = 0
    ptses.append(pts)

#把噪声点过滤掉，因为噪声点无法聚类，它们独自一类
corePoints = data[pandas.Series(ptses)!=0]

coreDist = euclidean_distances(corePoints)

#首先，把每个点的领域都作为一类
#邻域（Neighborhood）
#空间中任意一点的邻域是以该点为圆心、以 Eps 为半径的圆区域内包含的点集合
cluster = dict();
i = 0;
for row in coreDist: 
    cluster[i] = numpy.where(row<eps)[0]
    i = i + 1

#然后，将有交集的领域，都合并为新的领域
for i in range(len(cluster)):
    for j in range(len(cluster)):
        if len(set(cluster[j]) & set(cluster[i]))>0 and i!=j:
            cluster[i] = list(set(cluster[i]) | set(cluster[j]))
            cluster[j] = list();

#最后，找出独立（也就是没有交集）的领域，就是我们最后的聚类的结果了
result = dict();
j = 0
for i in range(len(cluster)):
  if len(cluster[i])>0:
    result[j] = cluster[i]
    j = j + 1

#找出每个点所在领域的序号，作为他们最后聚类的结果标记
for i in range(len(result)):
    for j in result[i]:
        data.at[j, 'type'] = i

plt.scatter(
    data['x'], 
    data['y'],
    c=data['type']
)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

3、实战案例：

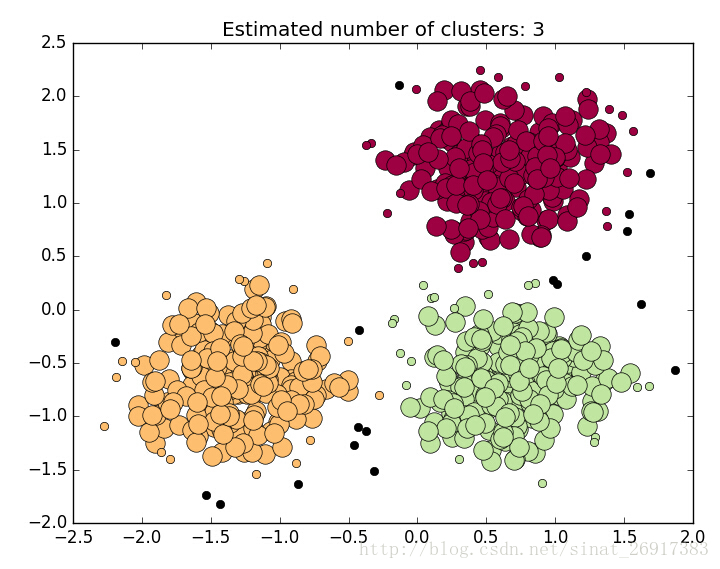
# DBSCAN clustering algorithm

print(__doc__)

import numpy as np

from sklearn.cluster import DBSCAN
from sklearn import metrics
from sklearn.datasets.samples_generator import make_blobs
from sklearn.preprocessing import StandardScaler

# Generate sample data
centers = [[1, 1], [-1, -1], [1, -1]]
X, labels_true = make_blobs(n_samples=750, centers=centers, cluster_std=0.4,
                            random_state=0)

X = StandardScaler().fit_transform(X)


# Compute DBSCAN
db = DBSCAN(eps=0.1, min_samples=10).fit(X)
core_samples_mask = np.zeros_like(db.labels_, dtype=bool)
core_samples_mask[db.core_sample_indices_] = True
labels = db.labels_

# Number of clusters in labels, ignoring noise if present.
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)

print('Estimated number of clusters: %d' % n_clusters_)
print("Homogeneity: %0.3f" % metrics.homogeneity_score(labels_true, labels))
print("Completeness: %0.3f" % metrics.completeness_score(labels_true, labels))
print("V-measure: %0.3f" % metrics.v_measure_score(labels_true, labels))
print("Adjusted Rand Index: %0.3f"
      % metrics.adjusted_rand_score(labels_true, labels))
print("Adjusted Mutual Information: %0.3f"
      % metrics.adjusted_mutual_info_score(labels_true, labels))
print("Silhouette Coefficient: %0.3f"
      % metrics.silhouette_score(X, labels))


# 
import matplotlib.pyplot as plt

# Black removed and is used for noise instead.
unique_labels = set(labels)
colors = [plt.cm.Spectral(each)
          for each in np.linspace(0, 1, len(unique_labels))]
for k, col in zip(unique_labels, colors):
    if k == -1:
        # Black used for noise.
        col = [0, 0, 0, 1]

    class_member_mask = (labels == k)

    xy = X[class_member_mask & core_samples_mask]
    plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
             markeredgecolor='k', markersize=14)

    xy = X[class_member_mask & ~core_samples_mask]
    plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
             markeredgecolor='k', markersize=6)

plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

最后的结果：

---

.

延伸一：DPEAK算法——密度最大值算法

本节来源：机器学习笔记（九）聚类算法及实践（K-Means,DBSCAN,DPEAK,Spectral_Clustering）、聚类 - 4 - 层次聚类、密度聚类(DBSCAN算法、密度最大值聚类)
密度最大值聚类是一种简洁优美的聚类算法, 可以识别各种形状的类簇, 并且参数很容易确定。用于找聚类中心和异常值的。
用DPEAK算法找到聚类中心之后，在用DBSCAN会更好

（1）我们首先给定一个半径范围r，然后对我们所有的样本，计算它的r邻域内的样本数目记作它的局部密度记作rho
（2）第二步，计算每个样本到密度比它高的点的距离的最小值记作sigma，有了这两个参数就可以进行我们下一步的筛选工作了

具体分成以下四种情况：
1 rho很小，sigma很大。这个样本周围的样本量很小，但是到比它密度大的点的距离还挺远的，这说明啥，它是个远离正常样本的异常值啊，在偏僻的小角落里搞自己的小动作啊，果断踢了它呀。
2 rho很大，sigma也很大。这个样本周围样本量很大，并且要找到比它密度还大的点要好远好远，这说明这个点是被众星环绕的啊，它就是这个簇的王，我们往往把它确定为簇中心。
3 rho很小，sigma也很小。样本周围的样本量很小，但要找到样本密度比它大的点没多远就有，说明这个点是一个处在边缘上的点，往往是一个簇的边界。
4 rho很大，sigma很小。该样本周围的样本量很大，但是密度比它还大的居然也不远，这种情况只会发生在你处在了簇中心的旁边时，很可惜，也许你是这个簇的核心成员，但你做不了这个簇的王。

好的，基于每个样本的rho和sigma，我们大概就能确定它们各自的所扮演的角色了，我们把大反派异常值从样本中剔除，然后把我们找到的rho和sigma都很大的点作为簇中心，再利用K-Means或者DBSCAN算法进行聚类就能得到相对比较好的结果。

---

延伸二：利用GPS轨迹和DBSCAN推断工作地居住地

来自文章《利用GPS轨迹和DBSCAN推断工作地居住地》
利用移动设备用户的GPS轨迹可以推断用户的工作地和居住地。本文中的数据集来自微软亚洲研究院的GeoLife GPS轨迹数据集

利用DBSCAN（Density-Based Spatial Clustering and Application with Noise）算法对数据集进行聚类。DBSCAN是一种聚类算法，这种算法通常用于对带有噪声的空间数据进行聚类。利用DBSCAN算法可以对GPS轨迹聚成4类。直观上来看，每一个聚类都表示该用户经常到访该区域。因此，可以假设用户的工作地和居住地就在这4个聚类中。

---

延伸三：HDBSCAN与Kmeans的聚类的一些纪要

HDBSCAN的安装与使用
安装的两种办法：

conda install -c conda-forge hdbscan  # first
pip install hdbscan    # second

 
 

 
 
1
2

应用：

import hdbscan
from sklearn.datasets import make_blobs

data, _ = make_blobs(1000)

clusterer = hdbscan.RobustSingleLinkage(cut=0.125, k=7)
cluster_labels = clusterer.fit_predict(data)
hierarchy = clusterer.cluster_hierarchy_
alt_labels = hierarchy.get_clusters(0.100, 5)
hierarchy.plot()

1
2
3
4
5
6
7
8
9
10
11

DBSCAN vs HDBSCAN
HDBSCAN - Hierarchical Density-Based Spatial Clustering of Applications with Noise. Performs DBSCAN over varying epsilon values and integrates the result to find a clustering that gives the best stability over epsilon. This allows HDBSCAN to find clusters of varying densities (unlike DBSCAN), and be more robust to parameter selection.

如果输入数据的变量类型不同，部分是数值型（numerical），部分是分类变量（categorical），需要做特别处理。

方法1是将分类变量转化为数值型，但缺点在于如果使用独热编码（one hot encoding）可能会导致数据维度大幅度上升，如果使用标签编码（label encoding）无法很好的处理数据中的顺序（order）。方法2是对于数值型变量和分类变量分开处理，并将结果结合起来，具体可以参考Python的实现[1]，如K-mode和K-prototype。

输出结果非固定，多次运行结果可能不同。

首先要意识到K-means中是有随机性的，从初始化到收敛结果往往不同。一种看法是强行固定随机性，比如设定sklearn中的random state为固定值。另一种看法是，如果你的K均值结果总在大幅度变化，比如不同簇中的数据量在多次运行中变化很大，那么K均值不适合你的数据，不要试图稳定结果 [2]

运行效率与性能之间的取舍。

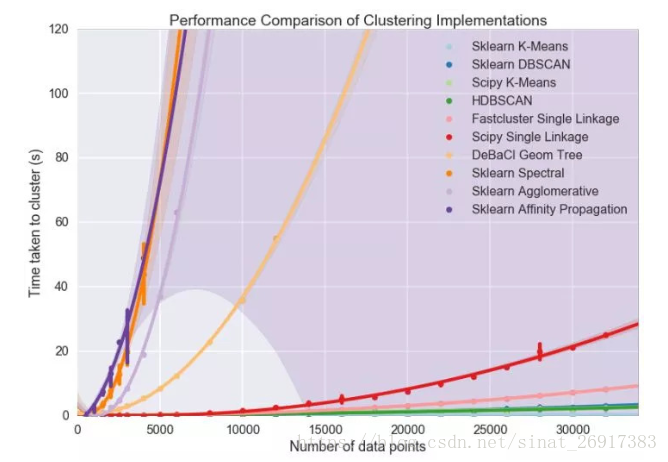
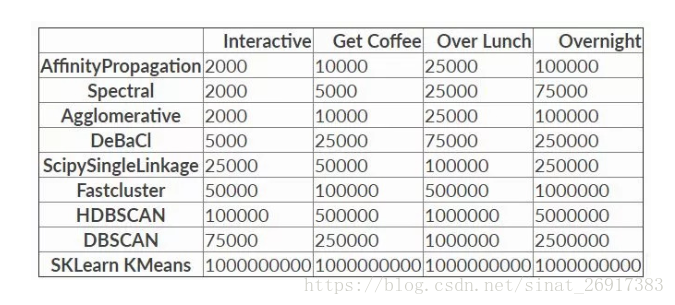
但数据量上升到一定程度时，如>10万条数据，那么很多算法都不能使用。最近读到的一篇对比不同算法性能随数据量的变化很有意思 [Benchmarking Performance and Scaling of Python Clustering Algorithms]。在作者的数据集上，当数据量超过一定程度时仅K均值和HDBSCAN可用。

因此不难看出，K均值算法最大的优点就是运行速度快，能够处理的数据量大，且易于理解。但缺点也很明显，就是算法性能有限，在高维上可能不是最佳选项。

一个比较粗浅的结论是，在数据量不大时，可以优先尝试其他算法。当数据量过大时，可以试试HDBSCAN。仅当数据量巨大，且无法降维或者降低数量时，再尝试使用K均值。

一个显著的问题信号是，如果多次运行K均值的结果都有很大差异，那么有很高的概率K均值不适合当前数据，要对结果谨慎的分析。

此外无监督聚类的评估往往不易，基本都是基于使用者的主观设计，如sklearn中提供的Silhouette Coefficient和 Calinski-Harabaz Index [5]。更多关于无监督学习如何评估可以参考 [微调：一个无监督学习算法，如何判断其好坏呢?]。

---

参考来源
聚类分析（五）基于密度的聚类算法 — DBSCAN
聚类算法第三篇-密度聚类算法DBSCAN
聚类算法初探（五）DBSCAN，作者: peghoty
聚类算法第一篇-概览
sklearn.cluster.DBSCAN
【挖掘模型】：Python-DBSCAN算法

其他：

https://blog.csdn.net/u013630675/article/details/80205663