矩阵论 - 10 - 四个基本子空间

四个基本子空间

四个子空间 Four subspaces

对于任意的 $m \times n$ 矩阵 $A$，若 $rank(A)=r$ ，则有：

• 行空间 $C(A^T)$

  • $A$ 的行向量的线性组合在 $\mathbb{R}^n$ 空间中构成的子空间，也就是矩阵 $A^T$ 的列空间。

  • $C(A^T) \in \mathbb{R}^n, dim C(A^T)=r$：

    行空间的基：将矩阵 $A$ 化为行阶梯矩阵：$A= \begin{bmatrix} 1 & 2 & 3 & 1 \\ 1 & 1 & 2 & 1 \\ 1 & 2 & 3 & 1 \\ \end{bmatrix} \underrightarrow{消元、化简} \begin{bmatrix} 1 & 0 & 1 & 1 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix} =R$

    行变换影响了 $A$ 的列空间，所以 $C(R) \neq C(A)$，但行变换并不影响行空间，所以可以在矩阵 $R$ 中看出前两行就是行空间的一组基。

    无论对于矩阵$A$还是$R$，其行空间的一组基，可以由行阶梯矩阵 $R$ 的前 $r$ 行向量组成。

• 零空间 $N(A)$

  • $Ax=0$ 的所有解 $x$ 在 $\mathbb{R}^n$ 空间中构成的子空间。
  • $N(A) \in \mathbb{R}^n, dim N(A)=n-r$，自由元所在的列即可组成零空间的一组基。

• 列空间 $C(A)$

  • $A$ 的列向量的线性组合在 $\mathbb{R}^m$ 空间中构成的子空间。
  • $C(A) \in \mathbb{R}^m, dim C(A)=r$，主元所在的列即可组成列空间的一组基。

• 左零空间 $N(A^T)$

  • 矩阵 $A^T$ 的零空间为矩阵 $A$ 的左零空间，是 $\mathbb{R}^m$ 空间中的子空间。

  • 为什么叫左零空间：$A^Ty=0 \rightarrow (A^Ty)^T=0^T\rightarrow y^TA=0^T$

  • $N(A^T) \in \mathbb{R}^m, dim N(A^T)=m-r$：

    左零空间的基：

    应用增广矩阵 $\left[\begin{array}{c|c}A_{m \times n} & I_{m \times n}\end{array}\right] \rightarrow \left[\begin{array}{c|c}R_{m \times n} & E_{m \times n}\end{array}\right]$

    将 $A$ 通过消元得到矩阵 $R$ ，其消元矩阵记为 $E$ 。

    则有 $EA=R$ (若 $A$ 为可逆方阵，则有 $E=A^{-1}$)

    例子：

    $$\left[\begin{array}{c|c}A_{m \times n} & I_{m \times m}\end{array}\right]=\left[\begin{array}{c c c c|c c c}1 & 2 & 3 & 1 & 1 & 0 & 0 \\1 & 1 & 2 & 1 & 0 & 1 & 0 \\1 & 2 & 3 & 1 & 0 & 0 & 1 \\\end{array}\right]\underrightarrow{消元、化简}\left[\begin{array}{c c c c|c c c}1 & 0 & 1 & 1 & -1 & 2 & 0 \\0 & 1 & 1 & 0 & 1 & -1 & 0 \\0 & 0 & 0 & 0 & -1 & 0 & 1 \\\end{array}\right]=\left[\begin{array}{c|c}R_{m \times n} & E_{m \times m}\end{array}\right]$$

    则

    $$EA= \begin{bmatrix} -1 & 2 & 0 \\ 1 & -1 & 0 \\ -1 & 0 & 1 \\ \end{bmatrix} \cdot \begin{bmatrix} 1 & 2 & 3 & 1 \\ 1 & 1 & 2 & 1 \\ 1 & 2 & 3 & 1 \\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 1 & 1 \\ 0 & 1 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix} =R$$

    很明显，式中 $E$ 的最后一行对 $A$ 的行做线性组合后，得到 $R$ 的最后一行，即 $0$ 向量，也就是 $y^TA=0^T$。

总结

四个子空间维度以及其之间关系可以参考Gilbert Strang的图：

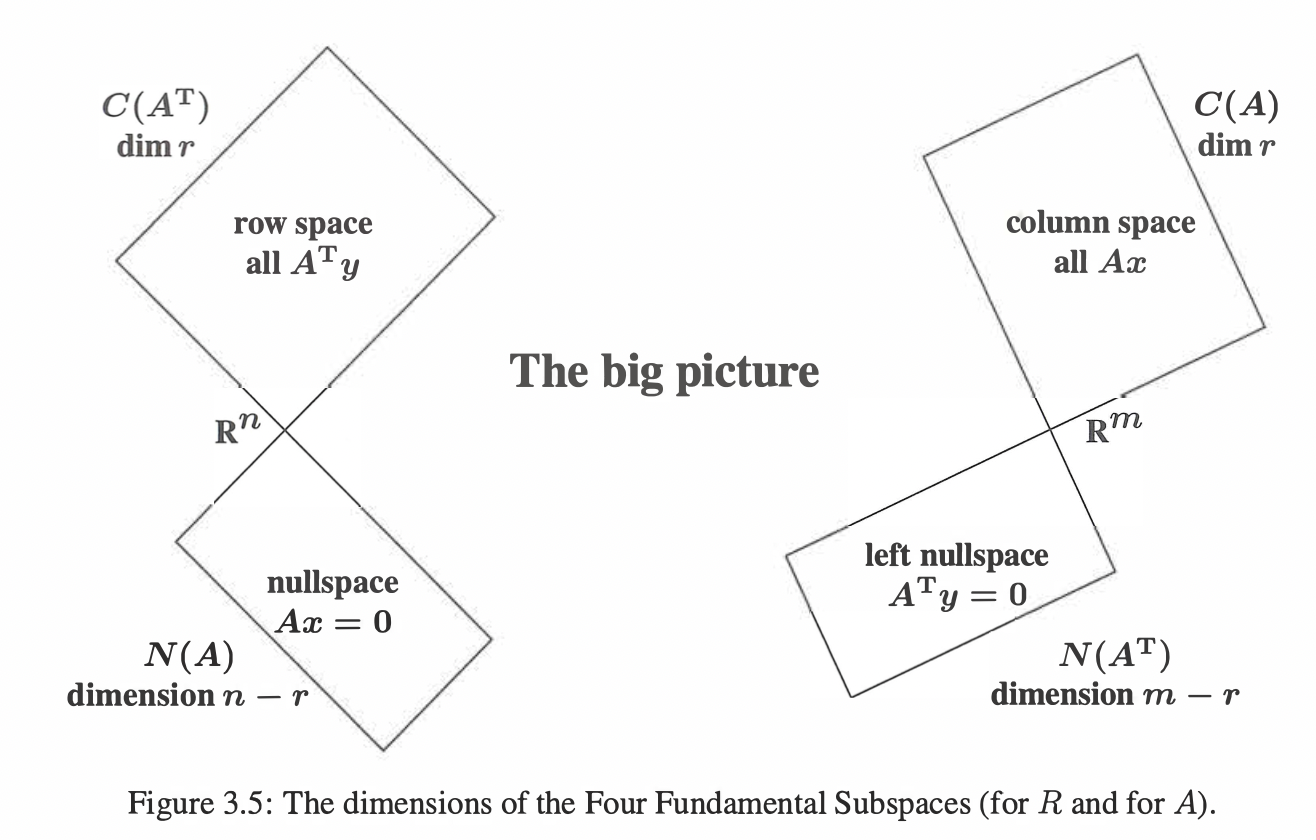
1. 行空间求法：将矩阵 $A$ 化为行阶梯矩阵，前 r 行向量。
2. 零空间求法：将矩阵 $A$ 化为行阶梯矩阵，得出自由列个数，自由列一个个赋1，其他皆0，求解方程，得出自由列个数个特解，特解的线性组合就是 $A$ 的零空间。
3. 列空间求法：主元所在的列即可组成列空间的一组基。
4. 左零空间求法：应用增广矩阵 $\left[\begin{array}{c|c}A_{m \times n} & I_{m \times n}\end{array}\right] \rightarrow \left[\begin{array}{c|c}R_{m \times n} & E_{m \times n}\end{array}\right]$ ，套用 $EA=R$ ，使得 $R$ 的某行为 $0$ 的$E$ 对应行向量。

reference

[1] textbook

[2] mit18.06学习笔记-0

[3] mit18.06学习笔记-1