【机器学习西瓜书学习笔记——决策树】

第四章 决策树

决策树分为分类树和回归树两种，分类树对离散变量做决策树，回归树对连续变量做决策树。

一棵决策树的生成过程主要分为以下3个部分：

• 特征选择： 是指从训练数据中众多的特征中选择一个特征作为当前节点的分裂标准，如何选择特征有着很多不同量化评估标准标准，从而衍生出不同的决策树算法。

• 决策树生成： 根据选择的特征评估标准，从上至下递归地生成子节点，直到数据集不可分则停止决策树停止生长。 树结构来说，递归结构是最容易理解的方式。

• 决策树剪枝： 决策树容易过拟合，一般来需要剪枝，缩小树结构规模、缓解过拟合。剪枝技术有预剪枝和后剪枝两种。

基本流程

划分选择，寻找最优划分属性

信息增益

信息熵：描述的是随机变量的不确定性（也就是混乱程度）。

假如决策树样本集为D，经过某属性划分后，样本集划分v个子集，D1,D2,…,Dv。
①我们先计算划分前D的信息熵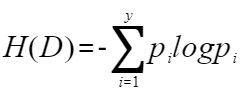

由于只有好瓜和坏瓜两种分类，所以y=2。pi表示第i类别的样本数占总样本数D的比例。

②然后我们计算划分后的子样本集的信息熵

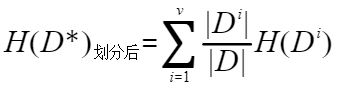
其中v是该属性的可取值的数量，比如划分属性为色泽，则v=3。Di表示该属性第i个值的样本数。相当于用色泽划分样本集D，样本集D中色泽=青绿的样本数。|Di|/|D|可以想象成一个权重。H(Di)的计算方法同计算H(D)的。

③信息增益：划分前的信息熵减去划分后的信息熵。其中a代表的此次划分中所使用的属性。

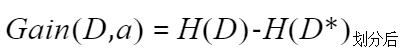
增益比

解决问题：矫正信息增益偏好的问题。

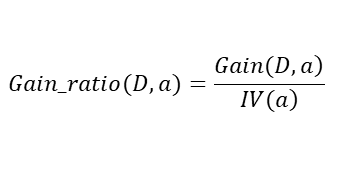
其中，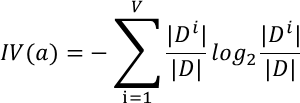

增益比就是信息增益除以IV(a)，IV(a)是属性a的固有属性，当属性a可取值增多的时候，IV(a)一般也增大，因此在一定程度上能抑制信息增益偏好取值多的属性的特点，但是增益比偏好取值较少的属性。

基尼指数

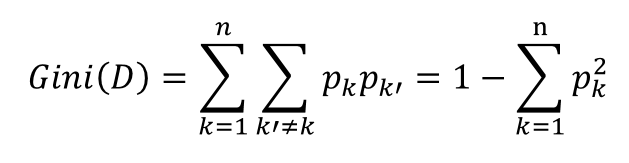
Gini（D）反映了从数据集D中随机抽取两个样本，其类别标记不一致的概率，因此Gini（D）越小，则数据集D的纯度越高。

基尼指数与信息熵虽然值不同，但是趋势一致。同样的，使用基尼指数来选择最优划分属性也是对比不同属性划分后基尼指数的差值，选择使样本集基尼指数减小最多的属性。

属性a的基尼指数定义为：使用划分前样本集D的基尼指数减去划分后子样本集Di的基尼指数加权和。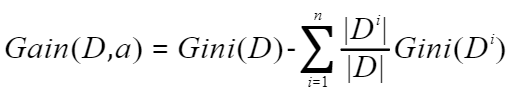

原理

以树形数据结构来展示决策规则和分类结果的模型，其重点是将看似无序、杂乱的已知实例，通过某种技术手段将它们转化成可以预测未知实例的树状模型，每一条从根结点（对最终分类结果贡献最大的属性）到叶子结点（最终分类结果）的路径都代表一条决策的规则。

基于信息论的三种决策树算法

划分数据集的最大原则是：使无序的数据变的有序。基于信息论的决策树算法有ID3 、C4.5和 CART等算法，其中C4.5和CART两种算法从ID3算法中衍生而来。

剪枝处理

剪枝处理目的——防止决策树过拟合。

剪枝分为“预剪枝”和“后剪枝”。两种操作的位置如下：

预剪枝

• 在决策树生成过程中，对每个结点在划分前先进行估计，若当前结点的划分不能带来决策树泛化性能提升，则停止划分并将当前结点标记为叶结点。
• 它的位置在每一次生成分支节点前，先判断有没有必要生成，如没有必要，则停止划分。

后剪枝

• 先从训练集生成一棵完整的决策树（相当于结束位置）。
• 然后自底向上的对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶结点，相当于将子树剪去。

值得注意的是，后剪枝时要用到一个测试数据集合，如果存在某个叶子剪去后能使得在测试集上的准确度或其他测度不降低（不变得更坏），则剪去该叶子。

优势：比预剪枝生成的效果好。

不足：时间复杂度大。

决策树回归

基本流程

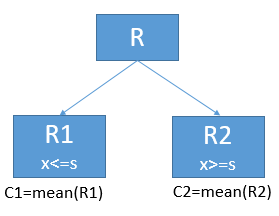
重点1：寻找最优切分点

回归决策树是通过最小二乘法来寻找最优切分点（j,s）的。首先寻找最优的C1使得R1的误差平方和最小，C2使得R2的误差平方和最小。

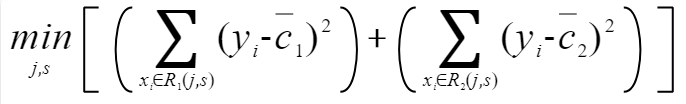
对于每一个（j,s），我们都会根据上式得到一个数值。然后我们取能使得上式取值最小的（j,s），作为最优切分点。

重点2：将样本切分后，子节点的输出值怎么算。

当找到最优切分点(j,s)后，将样本切分为左右两个子节点。子节点的输出值为该节点内的所有样本y的均值。

优缺点

优点

①易于理解和解释

②能够处理非线性关系

③对数据的缺失值不敏感

缺点

①容易过拟合

②不稳定性

③难以处理连续性特征

应用场景

• 金融领域：用于预测股票价格、货币汇率等金融指标。
• 医疗领域：用于预测疾病风险、药物反应等医疗相关问题。
• 工业领域：用于预测生产效率、设备故障率等工业数据。
• 零售领域：用于销量预测、市场需求分析等零售业务。

总结