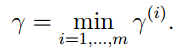Andrew Ng机器学习笔记+Weka相关算法实现（四）SVM和原始对偶问题_原始对偶算法实现

这篇博客主要讲解了Ng的课第六、七个视频，涉及到的内容包括，函数间隔和几何间隔、最优间隔分类器 （ Optimal Margin
Classifier）、原始/对偶问题 （ Primal/Dual Problem）、 SVM 的对偶问题几个部分。

• 函数间隔和几何间隔

函数间隔（ functional margin） 与几何间隔（ geometric margin）是理解SVM的基础和前提。
假设y∈{-1,1}，而不再是0,1，我们可以将分类器函数表示如下：

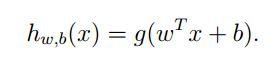
这里的b参数其实就是原来的X0，那么我们可以知道，W和B决定了一个确定的超平面。
给定一个训练样本，我们定义函数间隔：

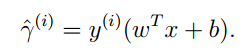
则当y(i)=1的时候，为了使函数间隔最大，我们要使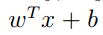取得一个较大的正数，当y(i)=-1时，我们要使得上式取到一个很小的负值。
接下来我们可以定义全局的函数间隔：

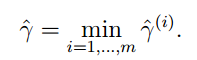
也就是说全局的函数间隔取决于函数间隔最小的那个样本点。
但同时也不难发现这里有一个问题，如果同时加大 w 和 b，则可以很容易的增加函数间隔，但是这样对实际求解是没有意义的的。我们为了限制 w 和 b，需要加入归一化条件。
接下来引入几何间隔：

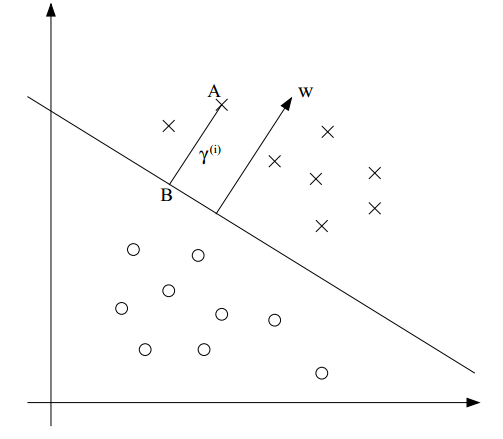
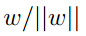
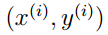
对于上面的图片，假设分割面上有一点B，它是A在这个分割面上的投影，这个间隔我们用γ表示，那么我们很容易知道BA的方向其实就是分割面的梯度方向。其单位向量是：，它的长度是1，方向和BA方向一致，那么我们假设A点的坐标是：，
这样我们不难表示出B点的坐标：

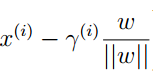
将坐标代入分割面方程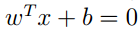
我们得到下式：

所以：

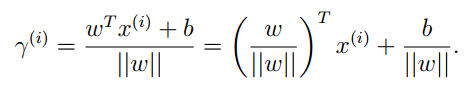
对于全局的γ，我们需要乘上类别：

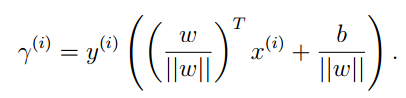
这就是点到平面的几何间隔，我们不难看出，当||W||=1时，几何间隔就是函数间隔。同样我们可以定义全局几何间隔：

• 最优间隔分类器

我们的目标是寻找到一个超平面，使得这个平面与离它最近的点距离最大，而不关心其他的点到平面的距离。
形式化表示如下：

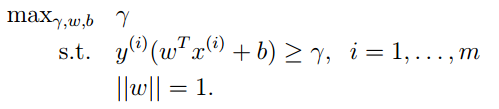
接下来的目标就是求得这个分割面的参数W和b，但是我们看到上述函数的约束条件是||W||=1，这是一个球面，典型的非凸优化问题，难以求解，我们要进行适当的变换。考虑几何间隔和函数间隔的关系：

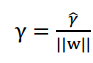
我们可以将原问题转化为：

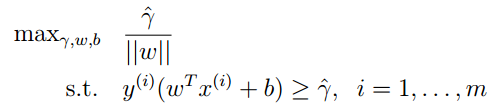
我们不妨再令：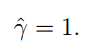
那么原问题就是求取1/||W||的最大值，也就是||W||平方的最大值，原问题进一步可以转化为下面问题：

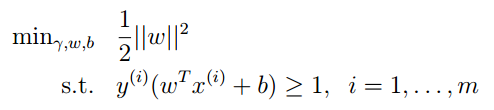
这个问题就变成了一个典型的二次规划问题，原问题变得可以求解。

• 拉格朗日对偶

为了求解上述问题，我们先看下一种最简单的等式约束：

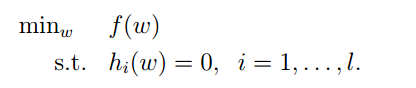
对于上述问题，我们一般可以用拉格朗日乘子法来求解，引入变量β：

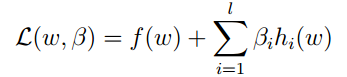
构造出上述拉格朗日乘式子，则原问题可以通过分别对W和β求偏导数

并令偏导数为0来求解出W和β。具体的数学证明就不在此讲解了，本科《微积分》都学过。
下面我们就是要将等式的情况推广到不等式，考虑到下面的求解问题：

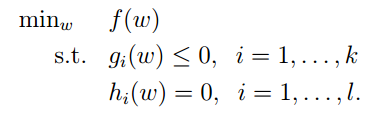
存在不等式约束条件，依然构造拉格朗日表达式：

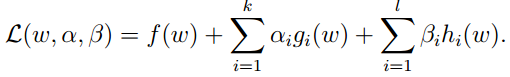
因为两个表达式，我们要引入αβ两个变量。
按照之前的求解方法，这个问题求解会遇到一个很大的问题：
因为g（W）<0，我们将α=正无穷，则表达式值变为负无穷，这样是没有意义的。因此我们必须避免这种情况，定义下式：

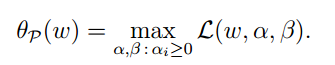
我们令α>0，则只有 g 和 h 满足约束时， θ(w)为 f(w)，也就是：

这样原问题求 min f(w)就等价于求minθ(w)。
我们令：

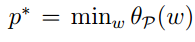
重新定义一个函数：

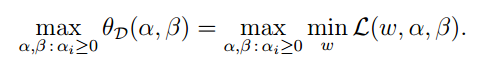
并令：

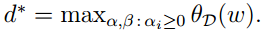
则有下列关系：

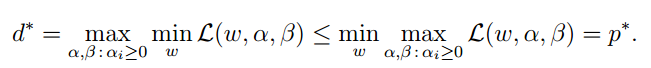
也就是最小值的最大值小于或等于最大值的最小值。这个问题是原问题的对偶问题，相对于原问题只是更换了 min 和 max 的顺序，在这里取等号，条件如下描述：

①假设约束不等式 gi都是凸 （ convex）函数（线性函数都属于凸函数）
②约束等式 hi 都是仿射（ affine）函数（形如h(w)=wTx+b）
③并且存在 w使得对于所有的 i，gi(W)< 0

在这些假设下，肯定存在 ω∗, α∗, β∗，使得ω∗是原始问题的解， α∗, β∗是对偶问题的解，且P∗ = d∗ = L(ω∗, α∗, β∗)。这样的ω∗, α∗, β∗需要满足 KKT（ Karush-Kuhn-Tucker）条件， KKT条件如下：

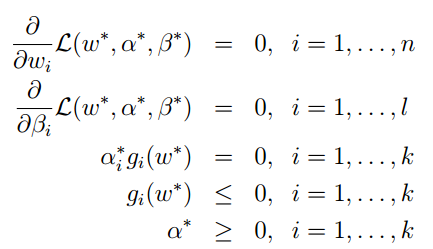
如果ω∗, α∗, β∗满足了库恩-塔克条件，那么他们就是原问题和对偶问题的解。
从上式可以看出来：
α∗> 0，那么gi(w∗) = 0。满足gi(w∗) = 0的w 处于可行域的边界上，这时候的W才能真正有用，内部的点，满足gi(w∗) <0都是没有意义的。这就引出了SVM的支持向量的概念。