- 1数据库总复习第十一章 并发控制_遵循两段锁协议的调度例题
- 2Tiny11作者开源:利用微软官方镜像制作独属于你的Tiny11镜像
- 3【灵境矩阵】零代码创建AI智能体之行业词句助手_智能体零代码和低代码
- 4手把手教你如何使用GitHub的服务器搭建自己的简单网站_github搭建网站 dns
- 5项目经理究竟一年能挣多少钱?一起来看看
- 6跨平台应用开发进阶(四十五)uni-app集成企微客服实战_uni-app进阶
- 7GPT-3不算机器学习算法创新?2020年AI顶会最佳论文榜单引发激烈争论
- 8【AI模型-机器学习工具部署】远程服务器配置Jupyter notebook或jupyter lab服务_jupyter 服务器
- 9Java、JavaScript以及python使用正则表达式校验用户的输入_用javascrip验证用户输入的个人信息:正则表达式经常被应用于对用户输入的信息进行
- 10【Android 构建新工具】Bazel 构建Android项目
【数据结构】排序(下)
赞
踩
二、常见排序的实现
8、快速排序的优化
当我们使用快速排序时,最坏的情况就是数组有序,此时的时间复杂度为O(N^2)
最好的情况就是key每次取中位数
所以我们为了避免最坏情况的发生,我们在快速排序的基础上衍生了一种优化的方法叫做三数取中
还有一种方法是随机选key,但随机选key的效果不如三数取中
int GetMidIndex(int* a, int left, int right) { int mid = (left + right) / 2; if (a[left] < a[mid]) { if (a[mid] < a[right]) return mid; else if (a[left] < a[right]) return right; else return left; } else { if (a[mid] > a[right]) return mid; else if (a[left] > a[right]) return right; else return left; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
将三个比较出中间的数字作为key然后换到left上,进行partsort
在每个partsort的最前边加上这条语句,就优化了这个快速排序的结构
int PartSort(int* a, int left, int right)
{
int midi = GetMidIndex(a, left, right);
Swap(&a[left], &a[midi]);
......
}
- 1
- 2
- 3
- 4
- 5
- 6
9、非递归快速排序
(1)基本思想
前边我们讲的快速排序是基于递归条件下实现的,但我们知道,递归会消耗栈上的空间,并且栈上的空间比较小,不能实现大量数据的快速排序,所以我们要将这个过程放在空间更大的堆上,也就是使用栈来实现
栈的作用就是存储区间,这个区间由两个整数组成,通过出入栈来模拟递归的过程
(2)代码实现
这里需要包含一下以前我们写过的栈的头文件
void QuickSortNonR(int* a, int left, int right) { Stack st; StackInit(&st); StackPush(&st,right); StackPush(&st, left); while (!StackEmpty(&st)) { int left = StackTop(&st); StackPop(&st); int right = StackTop(&st); StackPop(&st); //取出区间 int keyi = PartSort1(a, left, right); //通过keyi将数据区间一分为二 if (keyi + 1 < right) { StackPush(&st, right); StackPush(&st, keyi + 1); } if (left < keyi - 1) { StackPush(&st, keyi - 1); StackPush(&st, left); } //存入区间 } StackDestroy(&st); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
(3)时间复杂度
同递归方式的快速排序,为O(log₂N * N)
(4)空间复杂度
同递归方式的快速排序,为O(log₂N)
10、归并排序
(1)基本思想
将一个待排序的序列分为若干个子序列,每个子序列都是有序的,然后再将有序的序列合并为整体的有序序列
(2)代码实现
void _MergeSort(int* a, int left, int right, int* tmp) { if (left == right) return; //找到中间下标 int midi = (left + right) / 2; //一分为二二分为四的分开 _MergeSort(a, left, midi, tmp); _MergeSort(a, midi + 1, right, tmp); int begin1 = left, end1 = midi; int begin2 = midi + 1, end2 = right; //i用来记录容器数组中对应的下标 int i = left; //将两个数组中按升序归并到容器数组中 while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) tmp[i++] = a[begin1++]; else tmp[i++] = a[begin2++]; } //如果左右两个区间的数字还没有全部入到容器数组中,将它们按顺序输入 while (begin1 <= end1) tmp[i++] = a[begin1++]; while (begin2 <= end2) tmp[i++] = a[begin2++]; //将容器数组复制到原来的数组上 memcpy(a + left, tmp + left, sizeof(int) * (right - left + 1)); } void MergeSort(int* a, int n) { int* tmp = (int*)malloc(sizeof(int) * n); _MergeSort(a, 0, n - 1, tmp); free(tmp); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
(3)时间复杂度
归并排序分为两个过程
一是分解过程,这是一个类二叉树的过程,由中间下标分为两个区间,再分为四个区间,以此类推,此过程的时间复杂度是O(log₂N)
二是合并过程,合并过程中需要遍历整个数组,找到谁大谁小然后排序,这个过程的时间复杂度是O(N)
整个过程的时间复杂度就是O(N*log₂N)
(4)空间复杂度
该过程需要在堆上开辟n个空间,以及递归所需要的log₂n个在栈上的空间,由于对于n来说log₂n很小,所以它的空间复杂度为O(N)
11、非递归归并排序
(1)基本思想
与快速排序相同,递归方式的归并排序需要使用栈中空间,在处理大量数据时空间不够,所以我们可以用循环的方法减少栈的使用,这就是非递归的归并排序
(2)代码实现
void MergeSortNonR(int* a, int n) { int* tmp = (int*)malloc(sizeof(int) * n); int gap = 1; while (gap < n) { int j = 0;//作为tmp的下标 for (int i = 0; i < n; i += 2*gap)//每次跳过两组数据 { //这里的间隔差gap,每次比较两组数据 int begin1 = i, end1 = i + gap - 1; int begin2 = i + gap, end2 = i + gap * 2 - 1; //以下同上 if (end1 >= n || begin2 >= n) break; if (end2 >= n) end2 = n - 1; while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) tmp[j++] = a[begin1++]; else tmp[j++] = a[begin2++]; } while (begin1 <= end1) tmp[j++] = a[begin1++]; while (begin2 <= end2) tmp[j++] = a[begin2++]; memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1)); } gap *= 2;//while结束后把间隔调两倍 } free(tmp); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
(3)时间复杂度
for循环每次gap*=2,时间复杂度为O(log₂N),for循环中遍历了一遍数组,时间复杂度为O(N)
总的时间复杂度为O(N * log₂N)
(4)空间复杂度
申请了堆上的n个空间,空间复杂度为O(N)
12、非比较排序
(1)基本思想
计数排序是一种非比较排序,实现过程中不需要任何的比较
第一步:统计相同元素出现的次数
第二步:根据统计的结果将序列回收到原来的序列当中
这个排序适用于数据比较集中的序列
(2)代码实现
void CountSort(int* a, int n) { int min, max; min = max = a[0]; for (int i = 0; i < n; i++) { if (a[i] > max) max = a[i]; if (a[i] < min) min = a[i]; } int range = max - min + 1; //找到这一组数据中最大和最小的数相减得出这组数据的范围 int* countA = (int*)malloc(sizeof(int) * range); memset(countA, 0, sizeof(int)*range); //创建一个在堆上的数组作为计数数组,大小为这组数据的范围,将其中的元素全部重置为0 for (int i = 0; i < n; i++) countA[a[i] - min]++; //将每个数字出现的次数记录 int k = 0; for (int i = 0; i < range; i++) { while (countA[i]--) a[k++] = i + min; } }//下标加上整个数组的最小值就是当前数据的大小,countA为0时退出循环,不为0就记录下来
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
(3)时间复杂度
找出最大最小值需要遍历一遍数组,记录数字走for循环中range
所以时间复杂度为O(N+range),当数据比较集中时,时间复杂度接近O(N)
到底是O(N)还是O(range)取决于它们俩哪个大
(4)空间复杂度
在堆上开辟了range个空间,空间复杂度为O(range),当数据比较集中时,空间复杂度接近O(1)
三、各个排序方法所用时间的比较
1、代码实现
void TestOP() { srand(time(0)); const int N = 100000; int* a1 = (int*)malloc(sizeof(int) * N); int* a2 = (int*)malloc(sizeof(int) * N); int* a3 = (int*)malloc(sizeof(int) * N); int* a4 = (int*)malloc(sizeof(int) * N); int* a5 = (int*)malloc(sizeof(int) * N); int* a6 = (int*)malloc(sizeof(int) * N); int* a7 = (int*)malloc(sizeof(int) * N); int* a8 = (int*)malloc(sizeof(int) * N); for (int i = 0; i < N; ++i) { a1[i] = rand();//取随机值 a2[i] = a1[i]; a3[i] = a1[i]; a4[i] = a1[i]; a5[i] = a1[i]; a6[i] = a1[i]; a7[i] = a1[i]; a8[i] = a1[i]; //赋值给所有数据 } int begin1 = clock(); InsertSort(a1, N); int end1 = clock(); //clock是一个函数,用于记录当前时间点,在开始时记录一下,在结束后记录一下 //得出的时间差就是这个排序所用的时间 int begin2 = clock(); ShellSort(a2, N); int end2 = clock(); int begin3 = clock(); BubbleSort(a3, N); int end3 = clock(); int begin4 = clock(); SelectSort(a4, N); int end4 = clock(); int begin5 = clock(); HeapSort(a5, N); int end5 = clock(); int begin6 = clock(); QuickSort(a6, 0, N - 1); int end6 = clock(); int begin7 = clock(); MergeSort(a7, N); int end7 = clock(); int begin8 = clock(); CountSort(a8, N); int end8 = clock(); printf("InsertSort:%d\n", end1 - begin1); printf("ShellSort:%d\n", end2 - begin2); printf("BubbleSort:%d\n", end3 - begin3); printf("SelcetSort:%d\n", end4 - begin4); printf("HeapSort:%d\n", end5 - begin5); printf("QuickSort:%d\n", end6 - begin6); printf("MergeSort:%d\n", end7 - begin7); printf("CountSort:%d\n", end8 - begin8); free(a1); free(a2); free(a3); free(a4); free(a5); free(a6); free(a7); free(a8); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
2、分析
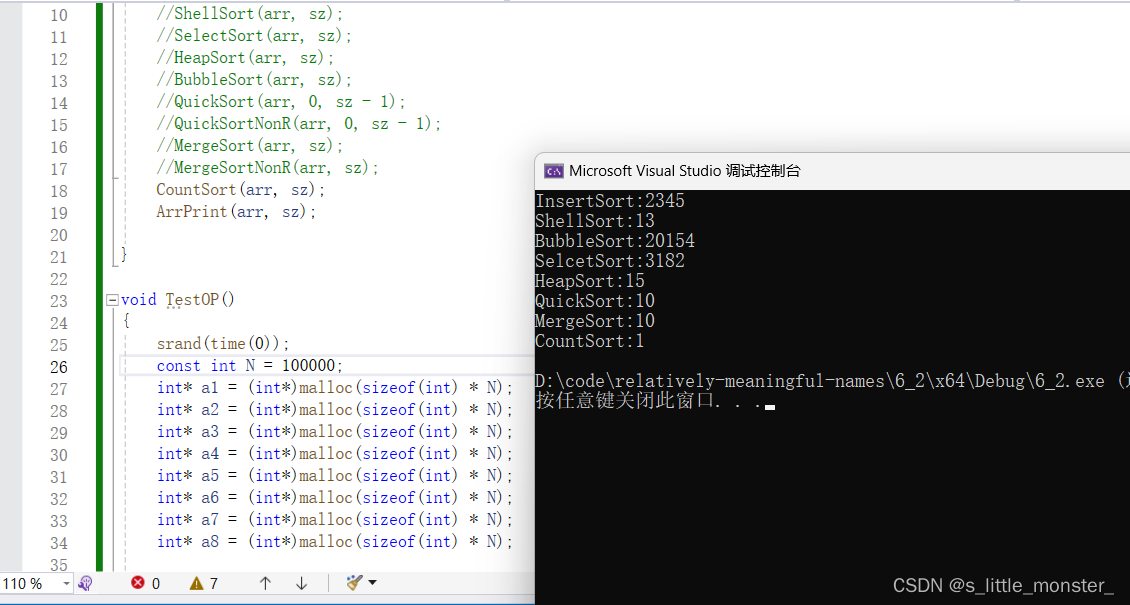
当数据给到10W个时,我们可以明显看出各个排序的差距
最拉胯的就是冒泡排序,跟其他排序所用时间都不在一个量级上
然后就是直接插入以及选择插入
然后就是希尔排序、堆排序、快速排序、归并排序
因为随机数的生成是由时间戳实现的,两个随机数之间差的并不多,所以范围比较集中,这就使得计数排序超级快
四、各个排序的稳定性
1、基本概念
稳定性好就是一个序列中存在着两个即两个以上的相同数据,这两个数据在排序前后相对位置不变,反之就是不好
这里的前后相对位置不变不是指它们两个数据一直待在原来的位置,而是前边的数字a1在排列后还在后边的数字a2前边,而不是跑到它的后边了
2、各个排序的稳定性复杂度一览表
| 排序方法 | 平均情况 | 最好情况 | 最坏情况 | 辅助空间 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(N^2) | O(N) | O(N^2) | O(1) | 稳定 |
| 简单选择排序 | O(N^2) | O(N^2) | O(N^2) | O(1) | 不稳定 |
| 直接插入排序 | O(N^2) | O(N) | O(N^2) | O(1) | 稳定 |
| 希尔排序 | O(N ^log₂N)~O(N ^2) | O(N^1.3) | O(N^2) | O(1) | 不稳定 |
| 堆排序 | O(N^log₂N) | O(N^log₂N) | O(N^log₂N) | O(1) | 不稳定 |
| 归并排序 | O(N^log₂N) | O(N^log₂N) | O(N^log₂N) | O(N) | 稳定 |
| 快速排序 | O(N^log₂N) | O(N^log₂N) | O(N^2) | O(log₂N)~O(N) | 不稳定 |
感谢观看





