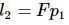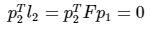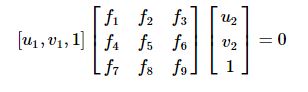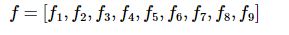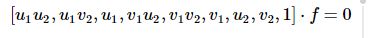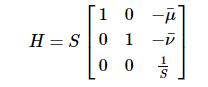计算机视觉——图像对的特征匹配及估计基础矩阵

基本矩阵F

基本矩阵是对极几何的代数表示，我们已经知道对于一幅视图上的点x，在另一视图上有一条对应的极线l’,该点的对应点x’必然在l’上，因此存在映射: x-> l’,基本矩阵F实际上就是表示这样的一种点到直线的射影映射

如图所示，考虑空间中不通过任何两个摄像机中心的平面pi,过第一个相机中心C和x的射线与该平面pi交于X,这个点再投影到第二幅图像上的点x’，这个过程通过平面pi的平移。由于X在对应与x的射线上，所以投影点x’必然在对应于这条射线的图像即极限l’上，点x和x’都是在一张平面上的3D点X的像，在第一幅图像上的所有点xi和对应点x’i的射影实际上是等价的，因为他们都射影等价于共面点集Xi，所以存在一个2D映射H,把每一个xi映射到x’i
给定点x’,通过x’和对极点e’的对极线I’，可以记为I’=e’ * x’ = [e’]x’，又因为x’=Hx，所以必然有
I’ = [e’]Hx = Fx

通过匹配点对估算基础矩阵

基础矩阵表示的是图像中的像点p1到另一幅图像对极线l2的映射，有如下公式：
而和像点P1匹配的另一个像点p2必定在对极线l2上，所以就有：
这样仅通过匹配的点对，就可以计算出两视图的基础矩阵F。
基础矩阵F是一个3×3的矩阵，有9个未知元素。然而，上面的公式中使用的齐次坐标，齐次坐标在相差一个常数因子下是相等，F也就只有8个未知元素，也就是说，只需要8对匹配的点对就可以求解出两视图的基础矩阵F。下面介绍下8点法 Eight-Point-Algorithm计算基础矩阵的过程。
假设一对匹配的像点p1=[u1,v1,1]T,p2=[u2,v2,1]T，带入式子中，得到：
把基础矩阵F的各个元素当作一个向量处理
那么上面式子可以写为
对于其他的点对也使用同样的表示方法。这样将得到的所有方程放到一起，得到一个线性方程组


求解上面的方程组就可以得到基础矩阵各个元素了。当然这只是理想中的情况，由于噪声、数值的舍入误差和错误的匹配点的影响，仅仅求解上面的线性方程组得到的基础矩阵非常的不稳定，因此在8点法的基础上有各种改进方法。
在实际计算中，可以直接用ATA的分解来求解参数。
也可以用非线性优化，通过搜索f使得||Af||最小化,同时满足||f||=1的约束
上述求解后的F不一定能满足秩为2的约束，因此还要在F基础上加以约束。

图像坐标归一化

将上面公式中由匹配的点对坐标组成的矩阵记为系数矩阵A
Af=0
系数矩阵A是利用8点法求基础矩阵的关键，所以Hartey就认为，利用8点法求基础矩阵不稳定的一个主要原因就是原始的图像像点坐标组成的系数矩阵A不好造成的，而造成A不好的原因是像点的齐次坐标各个分量的数量级相差太大。基于这个原因，Hartey提出一种改进的8点法，在应用8点法求基础矩阵之前，先对像点坐标进行归一化处理，即对原始的图像坐标做同向性变换，这样就可以减少噪声的干扰，大大的提高8点法的精度。

预先对图像坐标进行归一化有以下好处：
能够提高运算结果的精度
利用归一化处理后的图像坐标，对任何尺度缩放和原点的选择是不变的。归一化步骤预先为图像坐标选择了一个标准的坐标系中，消除了坐标变换对结果的影响。
归一化操作分两步进行，首先对每幅图像中的坐标进行平移（每幅图像的平移不同）使图像中匹配的点组成的点集的形心（Centroid）移动到原点；接着对坐标系进行缩放是的点p=(x,y,w)T中的各个分量总体上有一样的平均值，各个坐标轴的缩放相同的，最后选择合适的缩放因子使点p到原点的平均距离是。概括起来变换过程如下：
对点进行平移使其形心位于原点。
对点进行缩放，使它们到原点的平均距离为
对两幅图像独立进行上述变换。

上图左边是原始图像的坐标，右边是归一化后的坐标，H是归一化的变换矩阵，可记为如下形式：
其中，μ¯,ν¯是图像像点坐标两个分量的平均值<