十大经典排序算法与算法复杂度_十大排序算法时间复杂度

本系列算法整理自：https://github.com/hustcc/JS-Sorting-Algorithm
动图演示：https://www.runoob.com/w3cnote/ten-sorting-algorithm.html

排序算法是《数据结构与算法》中最基本的算法之一。

排序算法可以分为内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。

常见的内部排序算法有：插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。用一张图概括：

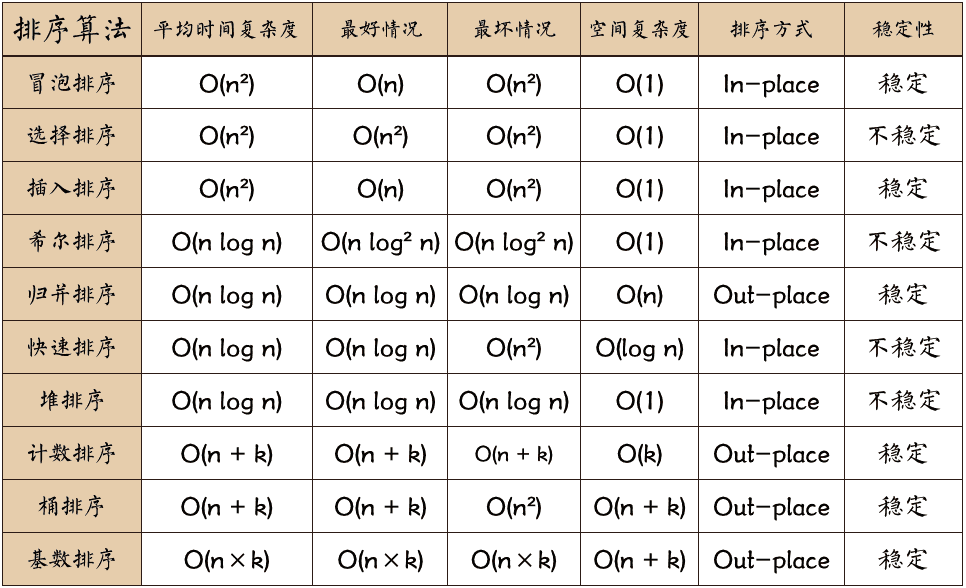
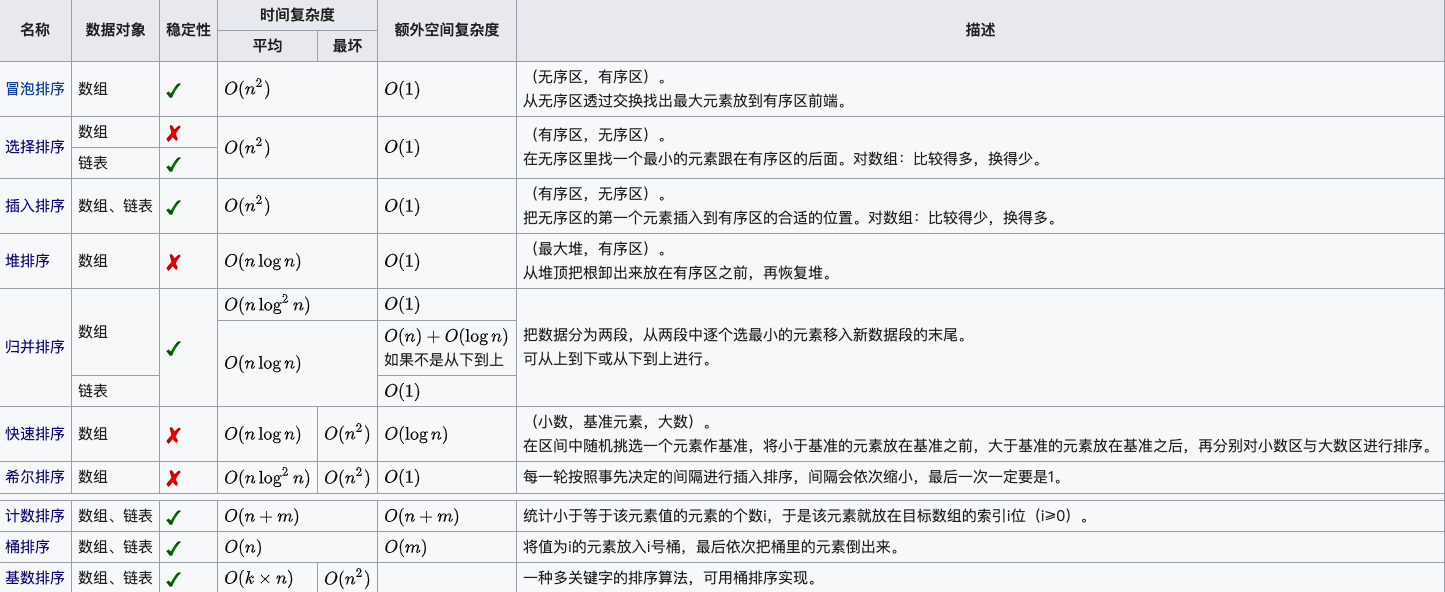
复杂度

主要还是从算法所占用的「时间」和「空间」两个维度去考量。

时间维度：是指执行当前算法所消耗的时间，我们通常用「时间复杂度」来描述。
空间维度：是指执行当前算法需要占用多少内存空间，我们通常用「空间复杂度」来描述。

参考：https://zhuanlan.zhihu.com/p/50479555

关于时间复杂度

平方阶 (O(n2)) 排序 各类简单排序：直接插入、直接选择和冒泡排序。

线性对数阶 (O(nlog2n)) 排序 快速排序、堆排序和归并排序；

O(n1+§)) 排序，§ 是介于 0 和 1 之间的常数。 希尔排序

线性阶 (O(n)) 排序 基数排序，此外还有桶、箱排序。

关于稳定性

稳定性的定义

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，ri=rj，且ri在rj之前，而在排序后的序列中，ri仍在rj之前，则称这种排序算法是稳定的；否则称为不稳定的。

稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序。

不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序。

名词解释：

n：数据规模
k："桶"的个数
In-place：占用常数内存，不占用额外内存
Out-place：占用额外内存
稳定性：排序后 2 个相等键值的顺序和排序之前它们的顺序相同

python

'''
# Create by LokiSharp(loki.sharp#gmail) at 2017-1-22
'''

TOTAL = 5000


def sortTest(func, total=1000):
    import random, copy, operator, math, time
    arrList = [i for i in range(-math.floor(total / 2), math.ceil(total / 2))]
    arrListR = copy.deepcopy(arrList)
    while operator.eq(arrList, arrListR):
        random.shuffle(arrListR)
    # print("--- [Origin List]", arrList, "Use", func.__name__,"with Total:", len(arrList))
    # print("--> [Random List]", arrListR, "Use", func.__name__,"with Total:", len(arrList))
    start = time.clock()
    arrListR = func(arrListR)
    end = time.clock()
    runtime = end - start
    # print("--> [Sorted List]", arrListR, "Use", func.__name__,"with Total:", len(arrList))
    if operator.eq(arrList, arrListR):
        print("[Success]", func.__name__, "with Total:", len(arrList), "in %.5fs" % runtime)
        return True
    else:
        print("[Fail]", func.__name__, "with Total:", len(arrList), "in %.5fs" % runtime)
        return False


def bubbleSort(arr):
    for i in range(1, len(arr)):
        for j in range(0, len(arr) - i):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
    return arr


def selectionSort(arr):
    for i in range(len(arr) - 1):
        # 记录最小数的索引
        minIndex = i
        for j in range(i + 1, len(arr)):
            if arr[j] < arr[minIndex]:
                minIndex = j
        # i 不是最小数时，将 i 和最小数进行交换
        if i != minIndex:
            arr[i], arr[minIndex] = arr[minIndex], arr[i]
    return arr


def insertionSort(arr):
    for i in range(len(arr)):
        preIndex = i - 1
        current = arr[i]
        while preIndex >= 0 and arr[preIndex] > current:
            arr[preIndex + 1] = arr[preIndex]
            preIndex -= 1
        arr[preIndex + 1] = current
    return arr


def shellSort(arr):
    import math
    gap = 1
    while (gap < len(arr) / 3):
        gap = gap * 3 + 1
    while gap > 0:
        for i in range(gap, len(arr)):
            temp = arr[i]
            j = i - gap
            while j >= 0 and arr[j] > temp:
                arr[j + gap] = arr[j]
                j -= gap
            arr[j + gap] = temp
        gap = math.floor(gap / 3)
    return arr


def mergeSort(arr):
    import math
    if (len(arr) < 2):
        return arr
    middle = math.floor(len(arr) / 2)
    left, right = arr[0:middle], arr[middle:]
    return merge(mergeSort(left), mergeSort(right))


def merge(left, right):
    result = []
    while left and right:
        if left[0] <= right[0]:
            result.append(left.pop(0));
        else:
            result.append(right.pop(0));
    while left:
        result.append(left.pop(0));
    while right:
        result.append(right.pop(0));
    return result


def quickSort(arr, left=None, right=None):
    left = 0 if not isinstance(left, (int, float)) else left
    right = len(arr) - 1 if not isinstance(right, (int, float)) else right
    if left < right:
        partitionIndex = partition(arr, left, right)
        quickSort(arr, left, partitionIndex - 1)
        quickSort(arr, partitionIndex + 1, right)
    return arr


def partition(arr, left, right):
    pivot = left
    index = pivot + 1
    i = index
    while i <= right:
        if arr[i] < arr[pivot]:
            swap(arr, i, index)
            index += 1
        i += 1
    swap(arr, pivot, index - 1)
    return index - 1


def swap(arr, i, j):
    arr[i], arr[j] = arr[j], arr[i]


def buildMaxHeap(arr):
    import math
    for i in range(math.floor(len(arr) / 2), -1, -1):
        heapify(arr, i)


def heapify(arr, i):
    left = 2 * i + 1
    right = 2 * i + 2
    largest = i
    if left < arrLen and arr[left] > arr[largest]:
        largest = left
    if right < arrLen and arr[right] > arr[largest]:
        largest = right

    if largest != i:
        swap(arr, i, largest)
        heapify(arr, largest)


def swap(arr, i, j):
    arr[i], arr[j] = arr[j], arr[i]


def heapSort(arr):
    global arrLen
    arrLen = len(arr)
    buildMaxHeap(arr)
    for i in range(len(arr) - 1, 0, -1):
        swap(arr, 0, i)
        arrLen -= 1
        heapify(arr, 0)
    return arr


def countingSort(arr, maxValue=None):
    bucketLen = maxValue + 1
    bucket = [0] * bucketLen
    sortedIndex = 0
    arrLen = len(arr)
    for i in range(arrLen):
        if not bucket[arr[i]]:
            bucket[arr[i]] = 0
        bucket[arr[i]] += 1
    for j in range(bucketLen):
        while bucket[j] > 0:
            arr[sortedIndex] = j
            sortedIndex += 1
            bucket[j] -= 1
    return arr

def radix_count(exp1):
    global list
    n = len(list)
    output = [0] * (n)
    count = [0] * (10)
    for i in range(0, n):
        index = (list[i] / exp1)
        count[(index) % 10] += 1
    for i in range(1,10):
        count[i] += count[i - 1]
    i = n - 1
    while i >= 0:
        index = (list[i]/exp1)
        output[count[(index) % 10] - 1] = list[i]
        count[(index) % 10] -= 1
        i -= 1
    i = 0
    for i in range(0,len(list)):
        list[i] = output[i]

def radixSort():
    global list
    max1 = max(list)
    exp = 1
    while max1 / exp > 0:
        radix_count(exp)
        exp *= 10


if __name__ == '__main__':
    sortTest(bubbleSort, TOTAL)
    sortTest(selectionSort, TOTAL)
    sortTest(insertionSort, TOTAL)
    sortTest(shellSort, TOTAL)
    sortTest(mergeSort, TOTAL)
    sortTest(quickSort, TOTAL)
    sortTest(heapSort, TOTAL)
    sortTest(radixSort, TOTAL)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216