深度学习（一）：卷积运算_深度卷积网络中卷积核的运算过程

一、卷积核与池化：

1.1 卷积核（Convolutional）：

将输入图像中一个小区域中像素加权平均后成为输出图像中的每个对应像素，其中权值由一个函数定义，这个函数称为卷积核(滤波器)。

一般可以看作对某个局部的加权求和；它的原理是在观察某个物体时我们既不能观察每个像素也不能一次观察整体，而是先从局部开始认识，这就对应了卷积。卷积核的大小一般有1x1,3x3和5x5的尺寸（一般是奇数x奇数）

1.2 池化（Pooling）：

卷积特征往往对应某个局部的特征。要得到global的特征需要将全局的特征执行ggregation（聚合）。池化就是这样一个操作，对于每个卷积通道，将更大尺寸（甚至是global）上的卷积特征进行pooling就可以得到更有全局性的特征。这里的pooling当然就对应了cross region

二、卷积层尺寸的计算原理:

2.1 卷积核输入输出层与卷积核的数量关系

        卷积核通道数 = 卷积输入层的通道数

        卷积核的个数 = 卷积输出层通道数(深度)

假设卷积输入层的输入是H x W x C, C是输入的深度(即通道数)，那么卷积核的通道数（层数/深度）也为C。

假设卷积核的大小为K x K，一个卷积核就为：K x K x C。

假设有P个K x K x C的卷积核，这样每个卷积核应用于输入都会得到一个通道，所以输出有P个通道。

例如：输入8x8x3（rgb三通道），输出是5位深度，卷积核尺寸为3x3。那么我们需要5个3x3x3的卷积核。每个卷积核共3层，每一层都是3x3。我们将一个卷积核的每一层（3x3）与原图的每一层（8x8）卷积，然后将得到三张新图叠加（算数求和），变成一张新的feature map。每个卷积核都这样操作，就可以得到5张新的feature map。具体运算过程可参照下图.

结论：不管输入图像的深度为多少，经过一个卷积核，最后都变成一个深度为1的特征图。不同的卷积核可以卷积得到不同的feature map。 

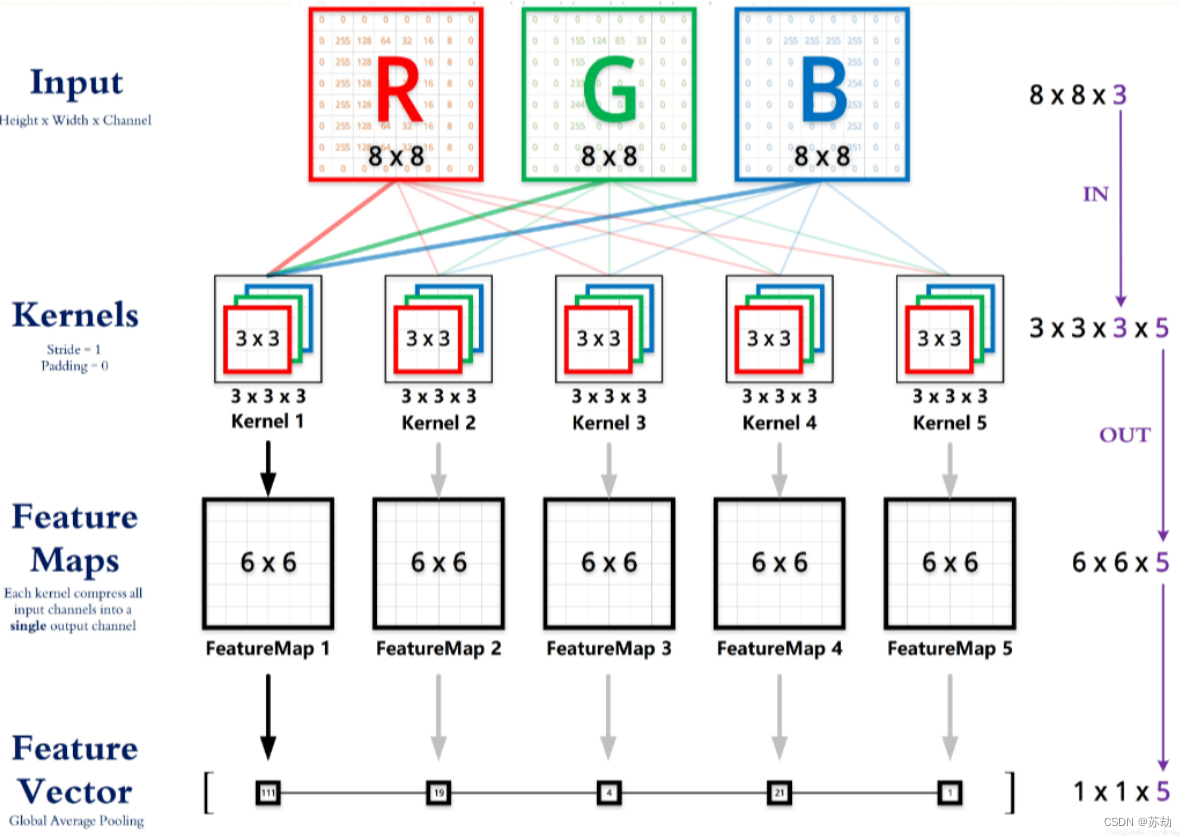
上图中6x6的结果是通过图2中所展示的运算公式得到的：

 

2.2 填充（padding）：

在输入特征图的每一边添加一定数目的行列，使得输出的特征图的长、宽 = 输入的特征图的长、宽

（1）填充的意义：

前面可以发现，输入图像与卷积核进行卷积后的结果中损失了部分值，输入图像的边缘被“修剪”掉了（边缘处只检测了部分像素点，丢失了图片边界处的众多信息）。这是因为边缘上的像素永远不会位于卷积核中心，而卷积核也没法扩展到边缘区域以外。

这个结果我们是不能接受的，有时我们还希望输入和输出的大小应该保持一致。为解决这个问题，可以在进行卷积操作前，对原矩阵进行边界填充（Padding），也就是在矩阵的边界上填充一些值，以增加矩阵的大小，通常都用“0”来进行填充的。通过填充的方法，当卷积核扫描输入数据时，它能延伸到边缘以外的伪像素，从而使输出和输入size相同。一般而言，用 0 进行填充。

（2）常用的两种填充：

• valid padding：不进行任何处理，只使用原始图像，不允许卷积核超出原始图像边界

• same padding：进行填充，允许卷积核超出原始图像边界，并使得卷积后结果的大小与原来的一致

2.3 步长（stride）：

滑动卷积核时，我们会先从输入的左上角开始，每次往左滑动一列或者往下滑动一行逐一计算输出，我们将每次滑动的行数和列数称为Stride，在之前的图片中，Stride=1；在下图中，Stride=2。

事实上，stride就是卷积核经过输入特征图的采样间隔。卷积过程中，有时需要通过padding来避免信息损失，有时也要在卷积时通过设置的步长（Stride）来压缩一部分信息，或者使输出的尺寸小于输入的尺寸。

Stride的作用：是成倍缩小尺寸，而这个参数的值就是缩小的具体倍数，比如步幅为2，输出就是输入的1/2；步幅为3，输出就是输入的1/3。

上面的说法（步幅为2，输出就是输入的1/2；步幅为3，输出就是输入的1/3）不是很严谨，这不是定理来的，步幅为2可以理解成对输入的特征图做了2倍下采样，我们希望的是减少输入参数，防止参数太多计算量太大，这是设置步幅为2的目的，并不是严格意义上的输出是输入的1/2、1/3，这里要特别弄清楚。

2.4 feature map的值的计算：

重合部分对应权值相乘相加，参考链接：3232548-ad8c1ead78877d28.gif (526×384) (jianshu.io)

图中，黄色部分的红色字体为卷积核对应权值，黑色字体为输入图像对应部分的值，将所有对应位置的值相乘相加，得到feature map如右图粉红色部分所示。

三、多通道卷积

事实上，在实际应用过程中，大多数输入图像都是 RGB 3通道。

3.1 卷积核与滤波器

卷积核（convolutional kernel）与滤波器（filter）

在只有一个通道的情况下，“卷积核”就相当于“filter”，这两个概念是可以互换的。

但在一般情况下（大多数输入图像都是 RGB 3通道），它们是两个完全不同的概念。每个“filter”实际上恰好是“卷积核”的一个集合，具体描述如下：

• 卷积核就是由长和宽来指定的，是一个二维的概念。

• 而过滤器是是由长、宽和深度指定的，是一个三维的概念。

• 过滤器可以看做是卷积核的集合。

• 过滤器比卷积核高一个维度——深度。

以前面的多通道卷积为例，卷积核的大小为3x3，卷积核的个数为3，此时：卷积核的维度为3x3，filter的维度为3x3x3。

事实上，我们仔细分析前面的卷积过程可以发现： 一个过滤器就对应一个特征图

3.2 多通道卷积

详细见2.1中的例子。