分支定价算法入门

分支定价法（branch and price）

组成

       ~~~~~~       分支定价由分支定界(branch and bound，B&B)和列生成算法(column generation)组成，它适用于求解大规模线性规划问题，其中B&B作为主体。branch and price的算法流程与B&B非常相似，不同的是在求解线性规划问题的过程中子节点采用column generation进行定界，通过削减变量减少复杂度，提高求解效率。

分支定界法

       ~~~~~~       作为五大算法之一，B&B可以解决整数线性规划和混合整数线性规划问题。通常单纯形法可以解线性规划的松弛模型，但是由于部分变量的整数约束条件，像$x\subseteq \mathbb{N}$或$x=0or1$，只求解松弛模型并未达到最终目标。
       ~~~~~~       这时候使用branch and bound在可行解空间中搜索，找出最优整数解，反应到数据结构中就是对二叉树进行搜索。

算法逻辑

1求解线性松弛的原问题
1.1 判断是否可行
a. 如果不可行，则原问题不可行
b. 如果可行，原问题得到整数解，线性松弛后的原问题的解是该问题的最优解，终止算法
c. 如果可行，线性松弛后的原问题没有得到整数解，则线性松弛后的原问题的目标函数值作为当前根节点的上界，选择原问题的可行解对应的目标函数值作为当前根节点的下界。根据分支策略进行分支得到子问题，并添加至未被探索的问题集中
2当未被探索的问题集不为空，且上下界的gap大于阈值，则根据搜索策略选择子问题进行探索
2.1 子问题不可行，剪枝
2.2 子问题可行
2.3 子问题得到整数解，子问题的线性松弛的解是该子问题的最优解，剪枝;线性松弛的子问题得到整数解，且线性松弛的子问题所求的目标函数值大于所有叶子结点的上界,算法终止
2.4 子问题没有得到整数解
当子问题的上界不超过原问题当前所求得的下界，剪枝。否则将线性松弛后的子问题的目标函数值作为当前根节点的上界，选择子问题的可行解对应的目标函数值作为当前节点的下界。根据分支策略进行分支得到子问题，并添加至未被探索的问题集中。
3算法的终止条件
当未被探索的问题集不为空；如果上界等于下界，或者上界-下界的gap很小，则算法终止。

列生成算法

列生成算法与单纯形法一样，是针对连续模型求解的（先将整数变量或者0-1变量松弛为连续变量得到松弛模型）。

1. 为什么使用列生成而不是单纯形法`
   在面对大规模问题时，变量数量极多，单纯形法寻找进基出基变量的速度非常慢，仅仅在寻找进基变量时，就需要对每一个非基变量进行reduced cost的计算，挑选最小的RC。（所谓reduced cost个人理解为某个变量使得目标函数下降的速度，对于优化方向为最小的问题来说，当然这个下降速度越快越好，因此需要寻找reduced cost的最小值）

2. 列生成法与单纯形法的关系
   个人认为列生成法就是单纯形法的改进版，它的优势主要体现在充分的削减变量，降低模型复杂度。相较于单纯形法在所有的变量里寻找最优策略，列生成算法首先寻找一组可行解，并将其余变量强制置零来生成一个小规模模型（RMP，restricted master problem），然后通过subproblem寻找要生成的列，加入到RMP中，直到不能寻找到使RC<0的列，此时，求解生成的RMP即可得到最优解。列生成算法流程图以及subproblem生成新列的方式均在下文中有所展示。

列生成算法流程

下面是列生成算法的简单流程图

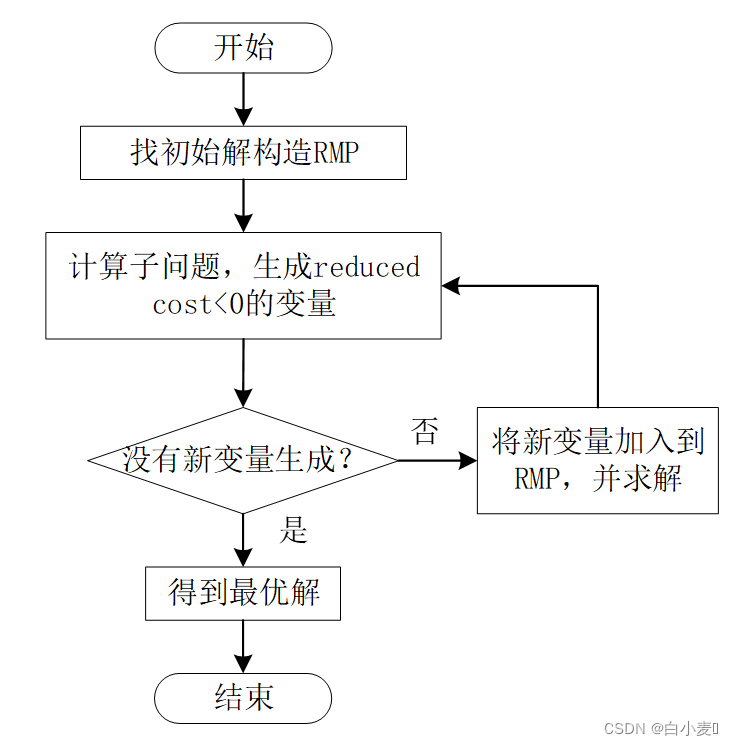
列生成算法要点

1.如何生成RMP
通常使用启发式算法寻找一个初始解，以经过启发式算法寻找的次优解构造RMP，在一定程度上也会加快求解速度。
2.subproblem建立
列生成算法中子问题的功能是寻找使reduced cost<0的列，将此列添加到RMP中，以进一步优化问题。因此它的目标函数即为检验数，检验数计算方法为$c_j-C_B{B}^{-1}{a}_j$ ，也就是变量$x_j$在主问题目标函数中对应的系数减去对偶变量与系数矩阵相乘。这里的$a_j$为主问题系数矩阵中对应变量$x_j$的系数，$c_j$为目标函数中$x_j$对应的系数，$C_B{B}^{-1}$为对偶变量组成的向量。另外，subproblem中还有约束，主要是对生成规则的约束，当然由于subproblem中的变量为待生成的主问题系数，因此这些约束自然也是针对这些系数的规则。比如在经典的纸卷生成问题中（cutting stock problem），各个切割方案长度的加和不能超过单个纸卷的总长度。
不了解cutting stock problem的小伙伴可以参考博客这位大佬的https://www.cnblogs.com/codejiaoer/archive/2021/11/24/Column_Geration.html，并且这篇博文还给出了具体的计算步骤，非常有助于理解。
3.subproblem的求解
subproblem求解也是一个优化问题，当然这比直接求解主问题要快多了，因为subproblem中的变量为系数，数量为约束的个数，所以变量数相较于主问题要少很多。话说回来，如果不快也不用这么麻烦了。