MATLAB 变换（Transforms）

MATLAB提供了用于处理诸如Laplace和Fourier变换之类的变换的命令。转换在科学和工程中用作简化分析和从另一个角度查看数据的工具。

例如，傅立叶变换允许我们将表示为时间函数的信号转换为频率函数。拉普拉斯变换使我们能够将微分方程转换为代数方程。

MATLAB提供laplace，fourier和fft变换命令来处理拉普拉斯，傅立叶和快速傅立叶变换工作的命令。

拉普拉斯变换

时间函数的拉普拉斯变换f(t)由以下积分给出-

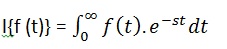
拉普拉斯变换也被称为变换f(t)来F(s)。您可以看到此转换或集成过程将f(t)符号变量t的一个函数F(s)与另一个变量s转换为另一个函数。

拉普拉斯变换将微分方程变成代数方程。要计算函数的拉普拉斯变换f(t)，请写入-

laplace(f(t))

实例

在此示例中，我们将计算一些常用函数的拉普拉斯变换。

创建一个脚本文件并输入以下代码-

syms s t a b w

laplace(a)
laplace(t^2)
laplace(t^9)
laplace(exp(-b*t))
laplace(sin(w*t))
laplace(cos(w*t))

运行文件时，它显示以下结果-

ans =
   1/s^2

ans =
   2/s^3

ans =
   362880/s^10

ans =
   1/(b + s)
  
ans =
   w/(s^2 + w^2)
  
ans =
   s/(s^2 + w^2)

拉普拉斯逆变换

MATLAB允许我们使用以下命令来计算拉普拉斯逆变换ilaplace。

例如，

ilaplace(1/s^3)

MATLAB将执行上述语句并显示结果-

ans =
   t^2/2

实例

创建一个脚本文件并输入以下代码-

syms s t a b w

ilaplace(1/s^7)
ilaplace(2/(w+s))
ilaplace(s/(s^2+4))
ilaplace(exp(-b*t))
ilaplace(w/(s^2 + w^2))
ilaplace(s/(s^2 + w^2))

运行文件时，它显示以下结果-

ans =
   t^6/720

ans =
   2*exp(-t*w)

ans =
   cos(2*t)

ans =
   ilaplace(exp(-b*t), t, x)

ans =
   sin(t*w)

ans =
   cos(t*w)

傅立叶变换

傅立叶变换通常将时间的数学函数变换f(t)为新函数，有时用或F表示，其参数是频率，单位为周/秒（赫兹）或弧度/秒。新函数然后称为傅里叶变换和/或函数f的频谱。

实例

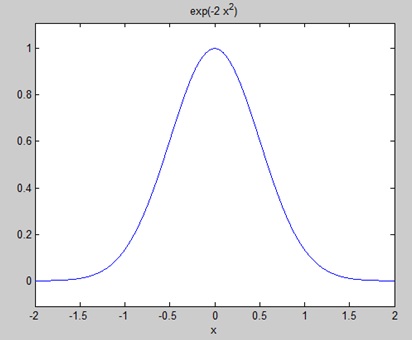
创建一个脚本文件并在其中键入以下代码-

syms x 
f = exp(-2*x^2);     %our function
ezplot(f,[-2,2])     % plot of our function
FT = fourier(f)      % Fourier transform

运行文件时，MATLAB绘制以下图形-

显示以下结果-

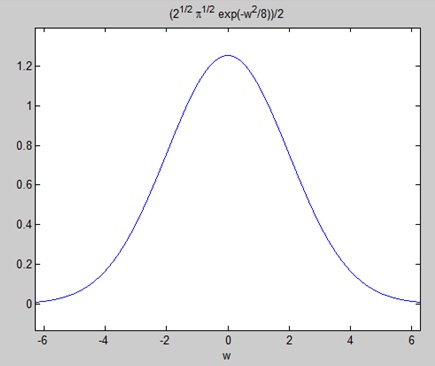
FT =
   (2^(1/2)*pi^(1/2)*exp(-w^2/8))/2

将傅立叶变换绘制为-

ezplot(FT)

给下图-

逆傅立叶变换

MATLAB提供了ifourier用于计算函数的傅立叶逆变换的命令。例如，

f = ifourier(-2*exp(-abs(w)))

MATLAB将执行上述语句并显示结果-

f =
   -2/(pi*(x^2 + 1))