- 1Python图像处理指南:PIL与OpenCV的比较_opencv pil
- 2数据仓库之DWD层
- 3carry4 的构成
- 4.Net接入AzureOpenAI、OpenAI、通义千问、智谱AI、讯飞星火、文心一言大语言模型。_qwen-max 下载
- 5今日份学习之Spring Boot 数据访问实现原理,太牛了_spri.g boot中访问数据库原理
- 6【蓝桥真题】三十块的蓝桥省赛模拟真题_蓝桥杯模拟赛出现过真题吗
- 7微信小程序 onReachBottom 上拉加载_小程序scroll-view onreachbottom
- 8AI、AGI、AIGC、ChatGpt 理解_什么是agi ugi
- 9pytest-入门
- 10基于Web Worker实现的附件上传(支持切片、暂停、闪传、续传,含前端具体代码以及简单的后端服务代码)_web端上传文件暂停
数字图像处理(3)—— 卷积_数字图像处理卷积运算
赞
踩
目录
1、卷积概述
卷积这个概念在很多领域中出现,比如信号与系统、数字信号处理、图像分类等等。那么什么是卷积?卷积有什么用?如何计算卷积呢?为了全面认识卷积,本文将从数学原理、物理意义等对卷积进行学习。
卷积是泛函分析中的一个数学算子,表示两个函数f,g经过翻转和平移变换后重叠部分的面积[1]。https://www.cnblogs.com/alexanderkun/p/8149059.html 这篇博客讲的已经很清晰了,大家可以参考一下。从学院派的角度来看待卷积这个计算,对于连续性方程,给出如下积分形式:
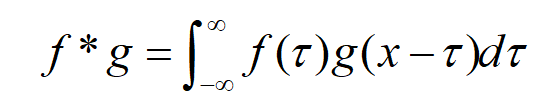
我们首先复习一下函数的变换,假设一个函数 f(x) ,则对于 f(x) 有以下的几何变换,假设变换存在:
| 函数 | 几何意义 |
| f(x) | 原始函数 |
| f(-x) | 关于 y 轴对称 |
| -f(x) | 关于 x 轴做对称 |
| f(x+a) a为任意实数 | f(x) 向左平移 a,若a为负,则为向右平移 |a| |
| f(x)+a a为任意实数 | f(x) 向上平移a,若a为负,则为向下平移 |a| |
| b*f(x) b 为任意正实数 | x 不变,y = y*b |
| f(bx) b 为任意正实数 | 在x轴上的伸缩变换 |
| f(x)g(x) g(x) 为一个函数 | 无实际的几何意义 |
人们常用于形容卷积计算的翻转的含义就可以理解了。对于两个函数 f(x) ,g(x) 定义卷积运算为:将 g(x) 翻转成为 g(-x),然后再进行平移 t 得到 g(-x+t) 则与 f(x) 乘积后的积分就是卷积了。
然后就是离散形式的卷积:

在信号与系统中,系统的零状态响应 = 激励 * 冲击响应(激励函数和冲击响应函数的卷积)。在图像处理中,也可以这样理解(这是我个人的看法),卷积后的图像就是输入图像与卷积核的卷积运算。一般图像的卷积作为滤波器,或者提取特征使用。
2、图像的卷积操作
2.1、基于 MATLAB 程序的图像卷积操作
之前我们提到,在MATLAB中,图像是以矩阵的形式存放的,那么对于矩阵的卷积操作是什么样的呢?推荐这篇:
https://blog.csdn.net/qq_38906523/article/details/80520950 ,讲解得非常清楚。
通常为了计算图像的卷积,需要将卷积核进行180°的旋转,然后把卷积核的中心与被计算像素点中心对齐。如果超出图像大小,则在边缘补 0。
- clear
- clf
- clc
- I = imread('lena.jpg');
- A = [1 1 1;1 1 1;1 1 1];
- B = [1 0 -1;1 0 -1;1 0 -1];
- C = [1 1 1;1 0 1;1 1 1];
- D = [1 1 1;0 1 1;0 0 1];
-
-
- subplot(2,2,1);
- imshow(imfilter(I,A,'replicate','same',conv));
- title('卷积核A');
-
- subplot(2,2,2);
- imshow(imfilter(I,B,'replicate','same',conv));
- title('卷积核B');
-
- subplot(2,2,3);
- imshow(imfilter(I,C,'replicate','same',conv));
- title('卷积核C');
-
- subplot(2,2,4);
- imshow(imfilter(I,D,'replicate','same',conv));
- title('卷积核D');



对于不同的卷积核,输出的图像情况不同。
2.2 基于OpenCV的数字图像卷积操作
原理不变。
- #include <opencv2\opencv.hpp>
- using namespace cv;
-
- int main()
- {
- Mat blurA,blurB,blurC,blurD;
- Mat img = imread("test.jpg"); // 载入一张图片
- // 定义卷积核
- float A[9] = { 1,1,1, 1,1,1, 1,1,1 };
- float B[9] = { 1, 0, -1, 1, 0, -1, 1, 0, -1 };
- float C[9] = { 1, 1, 1, 1, 0, 1, 1, 1, 1 };
- float D[9] = { 1, 1, 1, 0, 1, 1, 0, 0, 1 };
- // 卷积核改为矩阵
- Mat conv_kernel_A = Mat(3, 3, CV_32F, A);
- Mat conv_kernel_B = Mat(3, 3, CV_32F, B);
- Mat conv_kernel_C = Mat(3, 3, CV_32F, C);
- Mat conv_kernel_D = Mat(3, 3, CV_32F, D);
- // 卷积计算
- filter2D(img, blurA, img.depth(), conv_kernel_A);
- filter2D(img, blurB, img.depth(), conv_kernel_B);
- filter2D(img, blurC, img.depth(), conv_kernel_C);
- filter2D(img, blurD, img.depth(), conv_kernel_D);
-
- imshow("test", img); // 在窗口中显示载入的图片
- imshow("blurA", blurA);
- imshow("blurB", blurB);
- imshow("blurC", blurC);
- imshow("blurD", blurD);
- waitKey(0); // 等待按键按下退出
- return 0;
- }


参考
[1] https://baike.baidu.com/item/%E5%8D%B7%E7%A7%AF/9411006?fr=aladdin


