多元函数积分学

目录

一、二重积分

（1）二重积分的计算 

（1）二重积分的对称性

（2）华里士公式

二、三重积分

（1）直角坐标系下的计算：

（2）柱坐标系下的计算：

（3）球坐标系下的计算：

（4）三重积分的对称性：

（5）重积分的换元法：

三、曲线积分

（1）第一型曲线积分

 （2）第二型曲线积分

（3）一二型曲线积分关系

四、曲面积分

（1）第一型曲面积分

（2）第二型曲面积分

 （3）一二型曲面积分的关系

1、一二型曲面积分间的转化：

五、格林公式

 六、高斯公式

---

一、二重积分

（1）二重积分的计算 

1、极坐标法计算

极坐标法即为换元法的一种情况，其中x=rcosa，y=rcosa，此处的r为极径，而不是原来直接坐标系圆中的半径r，所以化为极坐标系始终有x^2+y^2=r^2

当二重积分的区域d为圆时且被积函数也为圆时，则区域d的4个像限内积分的结果一致，可以进行化简计算，即左区域面积为右区域的4倍

（1）二重积分的对称性

（2）华里士公式

 

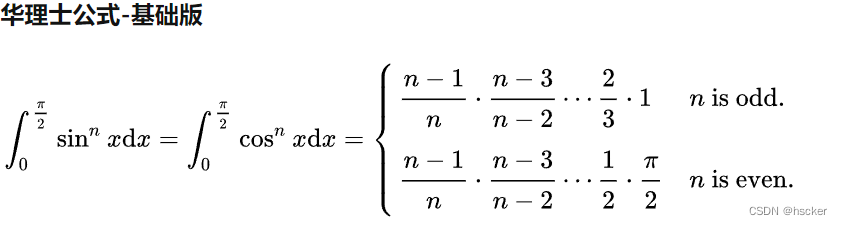
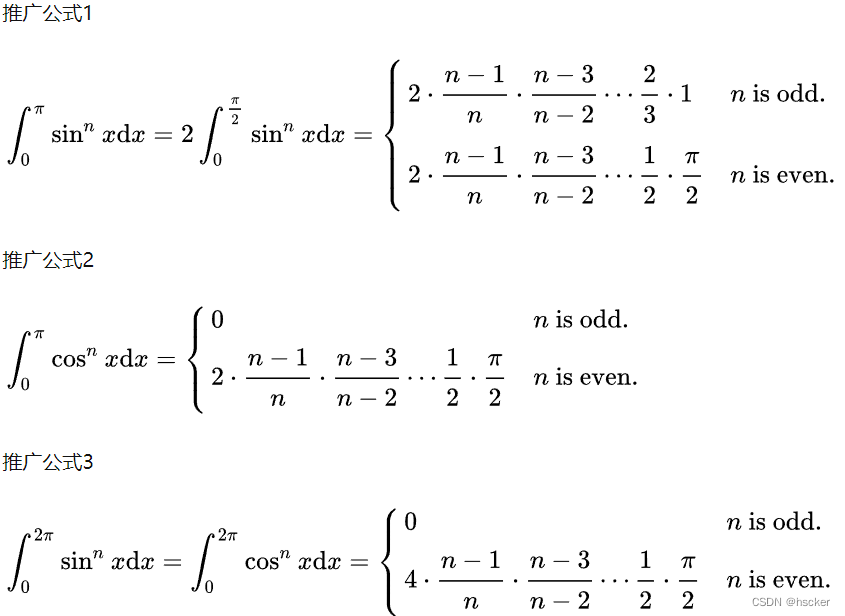
二、三重积分

（1）直角坐标系下的计算：

1、穿针法（先一后二，那么先求出z的上下限（不能含z），将被积函数对z积分后，则转为对二重积分的计算）

做法：沿平行z轴正方向穿针，穿入为下限z1，穿出为上限z2，投影到xoy面上，将z转为x与y后，计算投影在xoy面的二重积分（沿y轴或z轴同理）

理解：将物体分解为无数个大小质量不一的针（先一后二）

2、截面法（先把对应的单变量与其的积分提至左侧，之后求出面积且面积式子只能由单变量来表达，则转为对定积分的计算）

使用范围：适用于被积函数只有一个变量且截面面积很好求的情况（求的面积不是像穿针法那样投影的那个面，而是要适用于每一个截面）

做法：先确定被积变量的取值范围，后固定z（这样才将截面里的x，y用z表示），求每个截面的面积表达式

例如：积分区域为第一卦限的x^(2)+y^(2)+z^(2)=1，则每一片截面都有符合S=πr^2/4,又因为此时的r^2=x^2+y^2=z^2-1（此时的r对应的x与y在球面上，所以可以用x^2+y^2+z^2=1进行代换，这样求出来的截面才是对应的截面）,即完成把面积用z来表示

理解：将物体分解为无数个大小质量不一的面（先二后一）

例1（求三角形面积时，求边长时要到对应的平面内去求，此时就要根据特定的直线的方程式来求）

（2）柱坐标系下的计算：

使用范围：投影为圆的一部分，被积函数有f（x^2+y^2）形式

做法：穿针法的基础上，将z变为r与而不是x与y，将dxdydz=rddrdz

（穿针法，先一后二，先积z）

（3）球坐标系下的计算：

使用范围：积分区域为球/锥面，或被积函数为f（x^2+y^2+z^2）形式

三个参数：x=rcossin,y=rsinsin,z=rcos，记得换元后乘r^2sin

:投影到xoy面与x轴正方向的夹角

：固定，与整个z轴的夹角，由最小到最大

r：从原点引射线，穿过区域，穿入为下限，穿出为上限

 做法：先定后定最后定r的范围，后定的上下限可以含先定的未知数，反过来不可

（4）三重积分的对称性：

1、奇偶对称性：

积分区域关于xoy对称，则被积函数求关于z的奇偶函数，其他同理

2、轮换对称性：

积分区域的x与y互换，如果积分区域形式不变，则被积函数中可以进行相同轮换且积分值不变

（5）重积分的换元法：

1、二重积分的换元法：

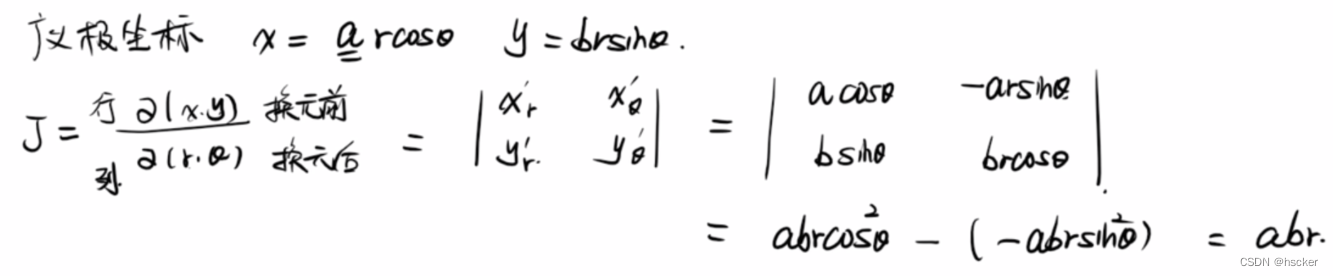
2、三重积分的换元法： （x,y,z对应1,2,3行,换元后的r,，z对应1,2,3列）

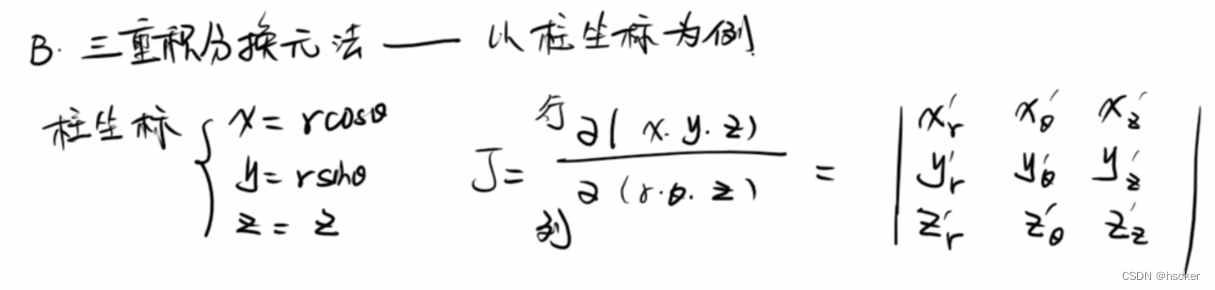
换元法（将原变量转换后，求出其对应的上下限替换，并且记得乘上雅克比行列式求出的对应参数）

例1、

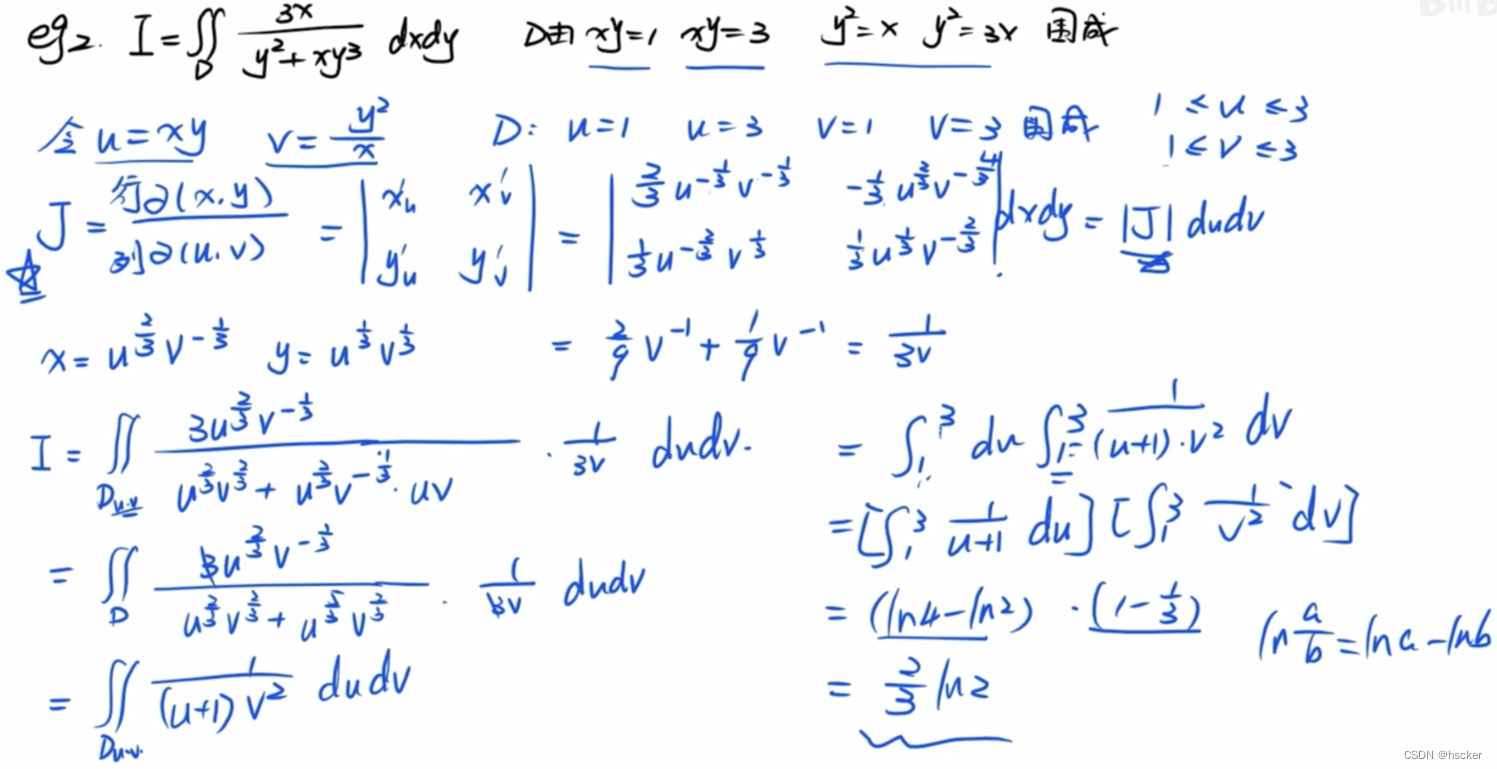
例2、

三、曲线积分

（曲线积分都要进行参数化）

（1）第一型曲线积分

1、性质：

对应的是弧长

2、计算方法：（一限二替三换积，一找单变量的上下限，二把被积函数全换为单变量，三替换ds为单变量的积分）

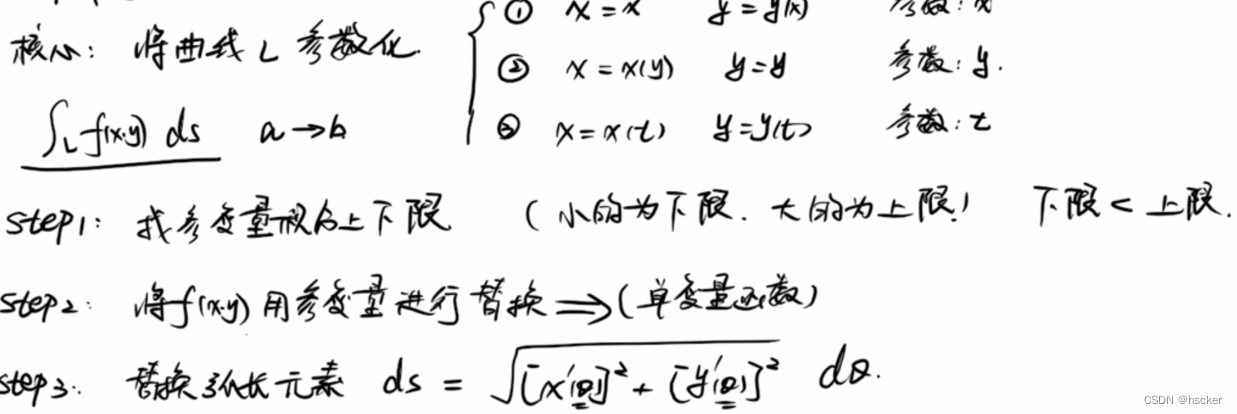
 3、对称性:

奇偶对称性：

曲线L关于x/y对称，被积函数关于y/x为奇/偶，则i=0/2i（曲线为原来轴对称后剩的一半）

轮换对称性：

L中x与y互换形式不变，则被积函数x与y互换积分结果也不变

例1（三变量的参数化）

 例2（对称性与弧长）

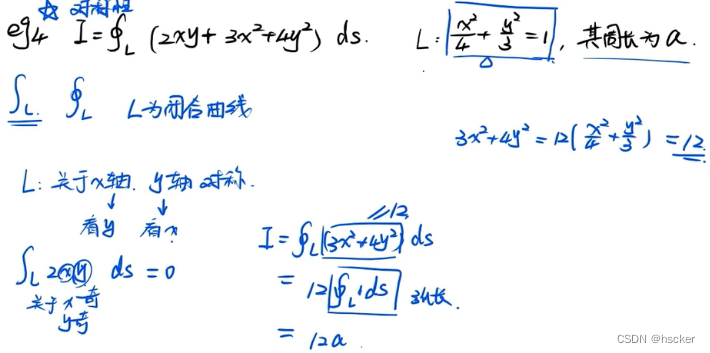
 （2）第二型曲线积分

1、计算方法：（同样是一限二替三换积）

例1

（3）一二型曲线积分关系

1、都要对某个参数（x,y,z,t等）进行参数化

2、前者下限必须小于上限，后者下对应起点，上对应终点

3、dx=cosads dy=cosbds，但由于二类积分有方向，所以cosa与cosb组成的单位切向量要考虑取正还是取负（两个函数分别是x对t的函数与y对t的函数，t为选择的参数）

4、后者的值与路径方向有关 

5、后者积的是dx与dy，而前者是ds

例1（一二类曲线积分的转化，正负取决于是否匹配，注意要单位切向量） 

四、曲面积分

（1）第一型曲面积分

1、计算方法：（一投二代三换，变为二重积分的计算，即ds转为dxdy）

2、对称性：（与三重积分一致，虽然是化为二重积分算，但他本来积分区域是曲面，这就涉及到三维，而二重积分积分区域是平面，只有二维）

奇偶：

曲面对于xoy对称，被积函数关于z奇或偶，其余2个面同理

轮换：

曲面方程中任意二个变量互换，曲面形式不变，则被积函数互换这两个变量，积分结果不变

例1

 例2（轮换对称性）

（2）第二型曲面积分

1、性质：

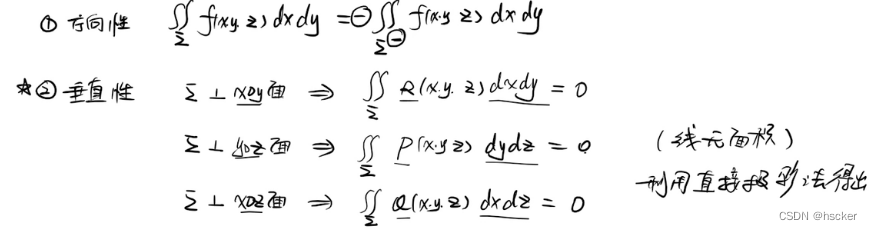
 2、计算方法：

（直接投影法）

（转换投影法）

3、总结：（曲线与曲面积分的积分式子）

有方向的积分都无对称性，无方向的积分都有对称性

 例1

例2（转换投影法）

 （3）一二型曲面积分的关系

1、一二型曲面积分间的转化：

 

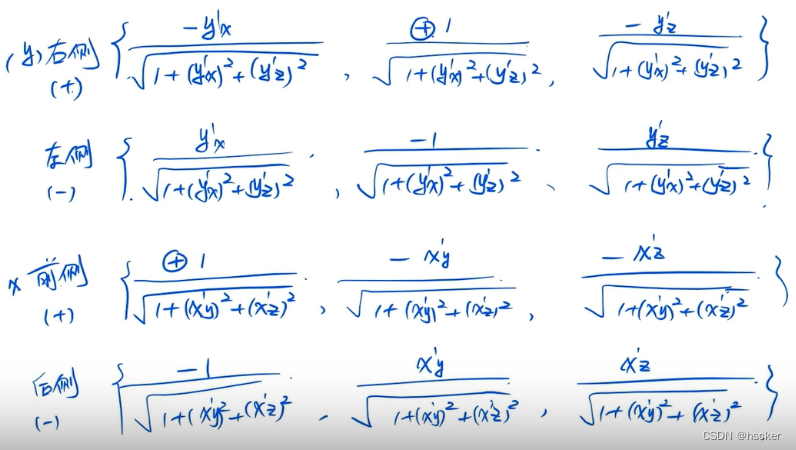
 向量对应上下侧，即把z对x与y求导求对应法向量，再根据上下侧判断取正负1，其他侧同理，用哪一种方法求，求得的都是该曲面的法向量，即方法不同结果一致

五、格林公式

（1）格林公式的计算：

 例1、 

例2、

（有奇点，则把他拆成两份，一份复连通，一份单连通来计算）

（2）格林公式的应用

1、四个等价条件

例1（用格林公式构造被积函数为常数的二重积分后计算第二项曲面积分间接求面积）

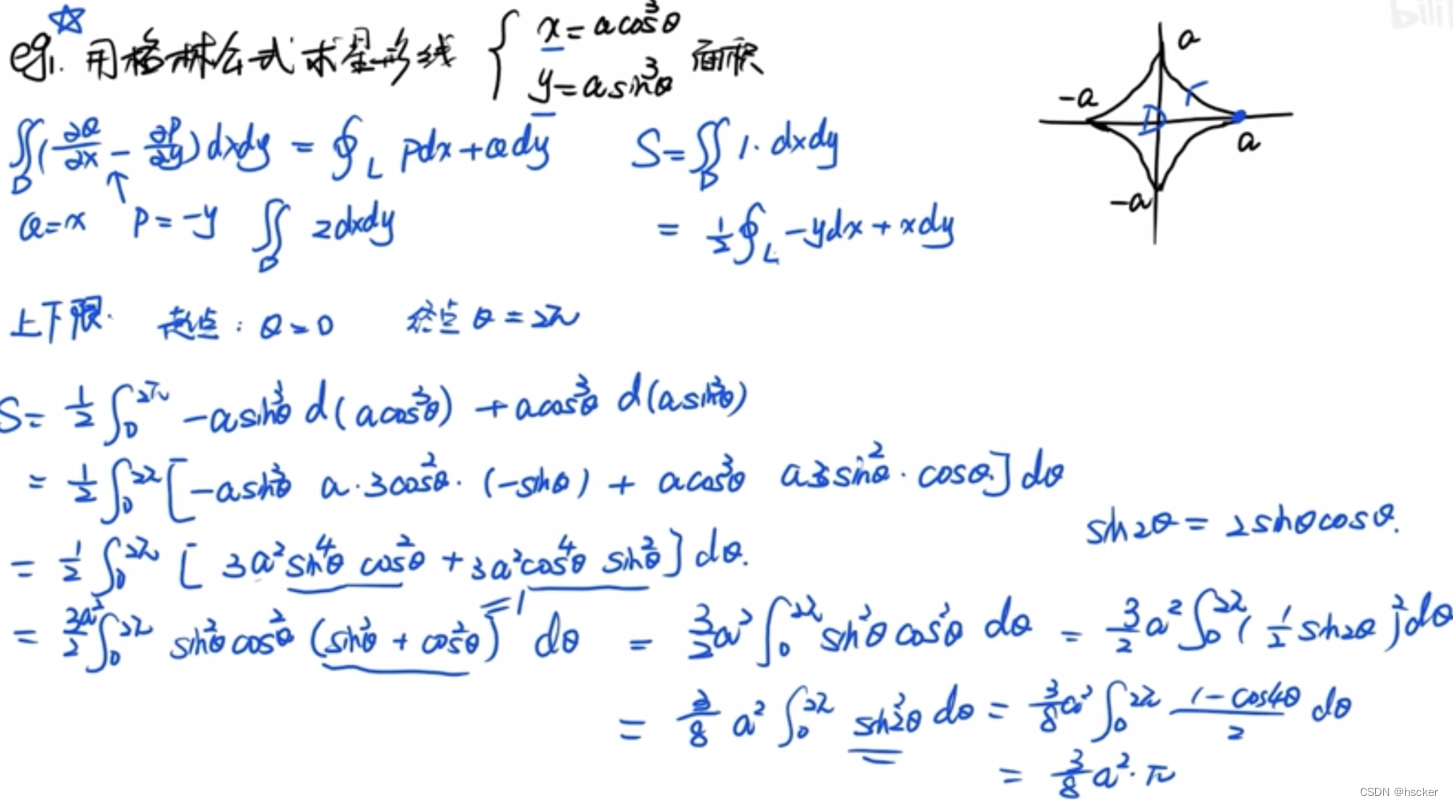
 例2（用格林公式性质1简化计算）

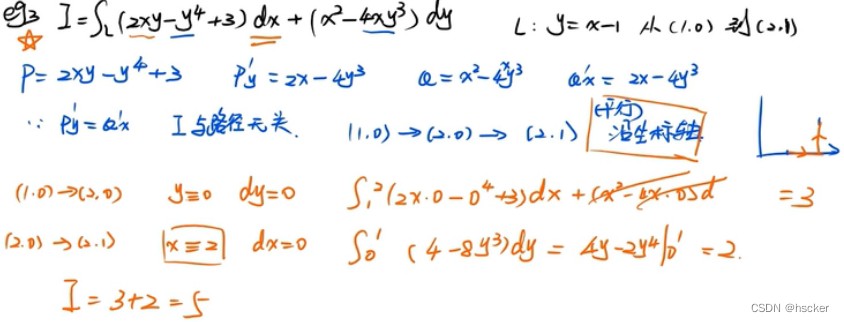
 六、高斯公式

1、介绍

例1（类比格林公式的挖洞法，同样要有内外相反的性质）

 例2（高斯公式一律以外侧为正，复连通时内曲面要内侧为正，格林公式则外逆内顺为正）