贝塞尔曲线，B-样条，非均匀有理B样条梳理_样条,b样条,贝塞尔

在一些最新的机器人的运动规划工作中，贝塞尔曲线、B样条、非均匀有理B样条常常被用来表征一条时空轨迹，取代了常用的时间多项式表征方法。这是因为贝塞尔曲线、B样条、非均匀有理B样条有一些优异的性质。是什么性质让以上三者在运动规划中大显身手，三者之间又有什么异同？这篇文章希望能够将这些概念讲清楚，希望对你有所帮助。

1. 贝塞尔曲线（Bézier curve）

1.1 一阶贝塞尔曲线

首先考虑这样一条曲线方程：
$$\mathbf{B}(t)={\mathbf{P}}_0+({\mathbf{P}}_1-{\mathbf{P}}_0)t=(1-t){\mathbf{P}}_0+t{\mathbf{P}}_1\text{\hspace{1em}(1)}$$
假设${\mathbf{P}}_0$,${\mathbf{P}}_1$是平面中的两点，则$\mathbf{B}(t)$代表平面中的一段线段，假设${\mathbf{P}}_0$,${\mathbf{P}}_1$是三维空间中的两点，则$\mathbf{B}(t)$代表三维空间中的一段线段。如图1所示：

图1 一阶贝塞尔动画示意图

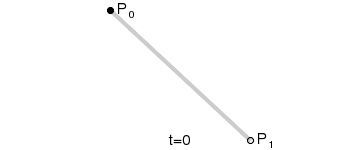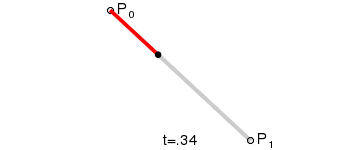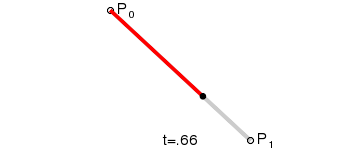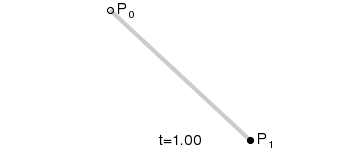
1.2 二阶贝塞尔曲线、高阶贝塞尔曲线

相应的，二阶贝塞尔曲线可以看成由空间中的三点${\mathbf{P}}_0$,${\mathbf{P}}_1$,${\mathbf{P}}_2$追踪，其对应曲线方程写为：
$$\mathbf{B}(t)=(1-t{)}^2{\mathbf{P}}_0+2t(1-t){\mathbf{P}}_1+t^2{\mathbf{P}}_2,t\in [0,1]\text{\hspace{1em}(2)}$$
二阶贝塞尔曲线的动画示意图如图2所示。

图2 二阶贝塞尔曲线动画示意图

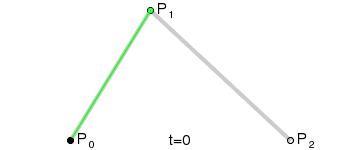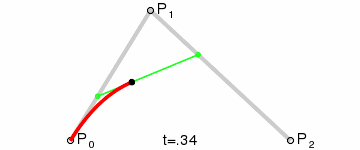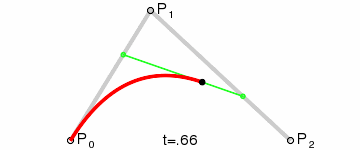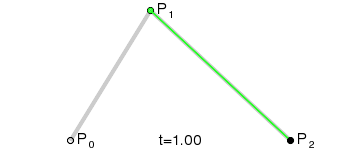
我们也可以这样理解二阶贝塞尔曲线，假设${\mathbf{Q}}_0$为${\mathbf{P}}_0$至${\mathbf{P}}_1$间的连续点，描述了一段线性（一阶）贝塞尔曲线${\mathbf{B}}_{{\mathbf{P}}_0{\mathbf{P}}_1}$, ${\mathbf{Q}}_1$为${\mathbf{P}}_1$至${\mathbf{P}}_2$间的连续点，描述了一段线性（一阶）贝塞尔曲线${\mathbf{B}}_{{\mathbf{P}}_1{\mathbf{P}}_2}$,则以${\mathbf{Q}}_1$，${\mathbf{Q}}_2$为控制点（路径点）的贝塞尔曲线方程可以写为：
$$\mathbf{B}(t)=(1-t){\mathbf{Q}}_0+t{\mathbf{Q}}_1\text{\hspace{1em}(3)}$$
式$(3)$与式$(2)$是完全等价的。式$(3)$给出了二阶贝塞尔曲线的递归形式，同理，对于三阶贝塞尔曲线，可以看成由四个空间中的控制点${\mathbf{P}}_0$,${\mathbf{P}}_1$,${\mathbf{P}}_2$，${\mathbf{P}}_3$，或是三个线性贝塞尔曲线描述点 ${\mathbf{Q}}_0$， ${\mathbf{Q}}_1$， ${\mathbf{Q}}_2$，或是两个二阶贝塞尔曲线描述点 ${\mathbf{R}}_0$, ${\mathbf{R}}_1$组成。三阶贝塞尔的曲线动画示意图如图3所示，其方程为：

$$\mathbf{B}(t)=(1-t{)}^3{\mathbf{P}}_0+3{\mathbf{P}}_{1}t(1-t{)}^2+3{\mathbf{P}}_2{t}^2(1-t)+{\mathbf{P}}_3{t}^3,t\in [0,1]\text{\hspace{1em}(4)}$$

图3 三阶贝塞尔曲线动画示意图

1.3 贝塞尔曲线的一般形式

至此，我们可以给出贝塞尔曲线的一般形式。假设空间中一条n阶贝塞尔曲线，则它被n+1个空间中的控制点唯一确定。具体曲线方程可以写为：

B ( t ) = ∑ i = 0 n ( n i ) P i ( 1 − t ) n − i t i = ( n 0 ) P 0 ( 1 − t ) n t 0 + ( n 1 ) P 1 ( 1 − t ) n − 1 t 1 + ⋯ + ( n n − 1 ) P n − 1 ( 1 − t ) 1 t n − 1 + ( n n ) P n ( 1 − t ) 0 t n , t ∈ [ 0 , 1 ] (5) \mathbf{B}(t)=\sum_{i=0}^{n}\left(

$$\begin{array}{c}n \\ i\end{array}$$ \right) \mathbf{P}_{i}(1-t)^{n-i} t^{i}=\left( $$\begin{array}{c}n \\ 0\end{array}$$ \right) \mathbf{P}_{0}(1-t)^{n} t^{0}+\left( $$\begin{array}{c}n \\ 1\end{array}$$ \right) \mathbf{P}_{1}(1-t)^{n-1} t^{1}+\cdots+\left( $$\begin{array}{c}n \\ n-1\end{array}$$ \right) \mathbf{P}_{n-1}(1-t)^{1} t^{n-1}+\left( $$\begin{array}{c}n \\ n\end{array}$$ \right) \mathbf{P}_{n}(1-t)^{0} t^{n}, t \in[0,1]\tag{5} B(t)=i=0∑n​(ni​)Pi​(1−t)n−iti=(n0​)P0​(1−t)nt0+(n1​)P1​(1−t)n−1t1+⋯+(nn−1​)Pn−1​(1−t)1tn−1+(nn​)Pn​(1−t)0tn,t∈[0,1](5)

我们可以将式$(5)$写为更简单的形式：
$$\mathbf{B}(t)=\sum _{i=0}^n{\mathbf{P}}_{\mathbf{i}}{\mathbf{b}}_{\mathbf{i},\mathbf{n}}(t),t\in [0,1]\text{\hspace{1em}(6)}$$

其中，${\mathbf{b}}_{\mathbf{i},\mathbf{n}}(t)$为伯斯坦因基底多项式，具体可写为：
b i , n ( t ) = ( n i ) t i ( 1 − t ) n − i ,   i = 0 , . . . n (7) \mathbf{b_{i,n}}(t)=\left(

$$\begin{array}{c}n \\ i\end{array}$$ \right) t^i(1-t)^{n-i}, \space i=0,...n \tag{7} bi,n​(t)=(ni​)ti(1−t)n−i, i=0,...n(7)

在式$(3)$中，我们推导了二阶贝塞尔曲线的递归形式，对于n阶贝塞尔曲线，我们可以将其写为更一般的形式：

$$\mathbf{B}(t)=(1-t){\mathbf{B}}_{{\mathbf{P}}_0{\mathbf{P}}_1...{\mathbf{P}}_{\mathbf{n}-1}}(t)+t{\mathbf{B}}_{{\mathbf{P}}_1{\mathbf{P}}_2...{\mathbf{P}}_{\mathbf{n}}}(t)\text{\hspace{1em}(8)}$$

对于式$(6)$，我们将${\mathbf{P}}_{\mathbf{i}}$称作贝塞尔曲线的控制点，将相邻的${\mathbf{P}}_{\mathbf{i}}$用线段相连，起于${\mathbf{P}}_0$，终于${\mathbf{P}}_{\mathbf{n}}$,如此形成的多边形称作贝兹多边形，由n+1个控制点所形成的n阶贝塞尔曲线被这些控制点所形成的贝兹多边形包的凸包所包含。如图4所示：

图4 贝塞尔曲线包含于贝兹多边形所形成的凸包

1.4 贝塞尔曲线的性质

在上文中，我们给出了贝塞尔曲线的定义、控制点的定义、贝塞尔曲线的递推形式以及贝兹多边形的凸包性质。贝塞尔曲线所具备的性质与这些定义息息相关，这些性质也是贝塞尔曲线能够被用到机器人运动规划中的主要原因。

给定空间中的一条n阶贝塞尔曲线以及它所依赖的n+1个控制点，则这条贝塞尔曲线具备这些性质：

1.终点插值特性：贝塞尔曲线起始于第0个控制点，终止于最后一个控制点，并绝不会经过其余控制点（除非所有控制点共线）

2.凸包特性：贝塞尔曲线被完整地限制在控制点所形成的凸包内

3.Hodograph: 贝塞尔曲线对时间微分所得到的曲线仍然是贝塞尔曲线，且新曲线的控制点可以用原有曲线的控制点表示:$c_i^{\prime }=n(c_{i+1}-c_i)$。其中，$n$为阶数，$c_i,c_{i+1}$为原始贝塞尔曲线的控制点，$c_i^{\prime }$为新曲线的控制点。

4.固定时间间隔特性: 一条贝塞尔曲线总是定义在固定时间间隔$t\in [0,1]$上。

1.5 贝塞尔曲线在运动规划中的应用

贝塞尔曲线在自主机器人运动规划中的应用价值基于以上四点特性，体现在如下几个方面上：

1.基于终点差值特性，我们可以设计一条由多段贝塞尔曲线组成的时空运动轨迹，每一段轨迹的的起止点就是由A*等前端路径规划方法找到的路径的转折点。

2.基于凸包特性，我们可以将每一段轨迹的控制点代入我们的碰撞位置约束方程内。假设每一段贝塞尔轨迹都有已经建立好的安全走廊，我们只要让每个控制点的每一维都在安全走廊对应维度的范围之内。这样，我们就能保证控制点所组成的凸包在安全走廊范围之内，从而整段贝塞尔轨迹都包含于安全走廊之内，没有碰撞风险。而不用一个一个采样点的去检查是否碰撞。如图5所示：

图5 贝塞尔轨迹位于安全走廊之内

3.基于Hodograph性质：由于贝塞尔曲线的微分也是贝塞尔曲线，同样具备终点插值特性与凸包性质。因此，位置曲线的微分得到速度曲线，其再次微分得到加速度曲线，皆为贝塞尔曲线，我们能够重复利用凸包性质保证其满足机器人的动力学约束。

2. B-样条（B-spline）

2.1 B样条定义

B样条曲线是贝塞尔曲线的一种一般化。我们知道，给定n+1个控制点，则贝塞尔曲线为n次的。对于B样条曲线来说则不是这样。假设空间中有m+1个控制点，则n次贝塞尔曲线可以写为：

$$\mathbf{S}(t)=\sum _{i=0}^m{\mathbf{P}}_i{b}_{i,n}(t),t\in [0,1]\text{\hspace{1em}(9)}$$

其中${\mathbf{P}}_{\mathbf{i}}$为控制点，${\mathbf{b}}_{\mathbf{i},\mathbf{n}}$为n次B样条基函数。m为区间数，n为样条曲线的次数，n取值可为$[2,m]$，即当曲线有m+1个控制点时，B样条基函数的次数可为2次到m次。

2.2 B样条基函数的定义

通过2.1节B样条定义我们可知，b样条基函数是组成B样条曲线的关键。那么，B样条基函数是如何定义的呢，它与组成贝塞尔曲线的伯斯坦因基底多项式又有何异同呢？

我们可以通过$Cox-deBoor$递归公式来定义m+1个n次B样条基：

b j , 0 ( t ) : = { 1 t j < t < t j + 1 0 … (10) b_{j, 0}(t):=\left\{

$$\begin{array}{ll}1 & t_{j}<t<t_{j+1} \\ 0 & \dots\end{array}$$ \right.\tag{10} bj,0​(t):={10​tj​<t<tj+1​…​(10)
$$b_{j,n}(t):=\frac{t-t_j}{t_{j+n}-t_j}{b}_{j,n-1}(t)+\frac{t_{j+n+1}-t}{t_{j+n+1}-t_{j+1}}{b}_{j+1,n-1}(t)\text{\hspace{1em}(11)}$$

从式10与式11我们可以知道，第$j$个控制点所对应的n次 B样条基只与与$[t_j,t_{j+n+1}]$共n+1个参数区间有关，即$b_{j,n}(t)$只在$[t_j,t_{j+n+1}]$不为0。

从相反的角度来说，$b_{j,n}(t)$的影响只存在于$[t_j,t_{j+n+1}]$这一段参数空间上。这与式（7）所定义的贝塞尔曲线中的伯斯坦因基地多项式是不同的，伯斯坦因及底多项式的每一项都会作用在整个参数空间上。

从上式我们也可以知道，若我们准备设计一条定义在参数空间$[t_s,t_f]$上的有m个控制点的n次B样条曲线，则我们需要把$[t_s,t_f]$划分为m+n个区间，即需要m+n+1个参数节点$[t_0,t_1,...t_{m+n+1}]$。注意，在不同的博客和资料中，所需要的节点数或许会有表达上的差异，这是因为部分资料中将n作为B样条基函数的阶数=次数+1，因此所需的参数节点即变为:m+n,也就是：控制点个数+阶数；

2.3 B样条基函数的定义域

由于我们定义的B样条基函数是n次n+1阶的，因此，合法的定义域上应该要有n+1个基函数（亦即控制点）与其对应。虽然我们将参数轴划分为m+n+1节点，m+n个参数区间，但并不是所有区间上都定义有足够的基函数。
如图6所示，考虑一个有五5个顶点，4阶的B样条曲线，则其合法的定义域应该为：$[u_3,u_5]$（定义有4个控制点）

图6 B样条曲线定义域示意图

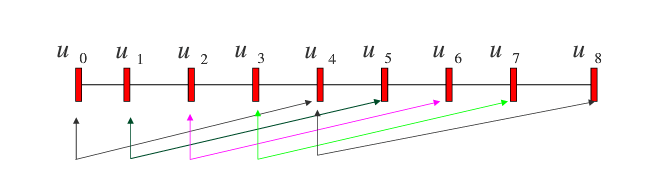
更一般的，对于一个m个顶点，n次的B样条曲线，其合法定义区间为：$[u_n,u_m]$

例：一个具备14个顶点，6次的B样条曲线，则其节点数应为：14+6+1=21.假设节点的分布为均匀的，则节点序列为[0.05,0.1,…0.95,1]的合法定义区间为[0.3,0.7],一个符合要求的B样条曲线如图7所示：

图7 B样条曲线定义域示意图2

2.4 B样条基函数重要参数

在上一节中，我们已经对B样条，B样条基函数做出了完整的解释。在这里，我们重新梳理一下定义B样条曲线所需要的参数：

1. 定义域$t\in [t_s,t_f]$，一般为时间轴
2. 控制点$P_i$,共m个
3. B样条基函数次数n
4. 节点数量：m+n+1

2.4 B样条基函数性质：

B样条基函数有以下重要性质：

1.$b_{i,n}(t)$是在t上的n次多项式。

2.非负性：对于所有的$i,n,t$，$b_{i,n}(t)$为非负的。

3.局部支撑或局部作用：$b_{i,n}(t)$定义在$[t_I,t_{i+n+1}]$上，并只对定义区间内的曲线施加影响。

4 权和性：所有非零的n次基函数在区间$[t_i,t_{i+1}]$上的和为1

5 连续性： 在一个有重复度k的节点处，基函数$b_{i,n}(t)$是$C^{n-k}$连续的。

2.5 B样条曲线性质：

在得到B样条基函数性质后，B样条曲线的性质也就显而易见了：

1.具有m个控制点，n次的B样条曲线应具备m+n+1个节点，定义在$[t_n,t_m]$上。

2.凸包性：样条曲线包含在控制折线所形成的凸包内。

3.局部作用：第i个控制点$P_i$只影响区间$[t_i,t_{i+n+1}]$上的曲线。

4.Hodograph: B样条曲线的微分得到的是低一阶的B样条曲线。

5.在一个有重复度k的节点处，基函数$b_{i,n}(t)$是$C^{n-k}$连续的。

2.6 运动规划中B样条曲线与贝塞尔曲线的异同

相比较与贝塞尔曲线，B样条曲线同样具备贝塞尔曲线凸包、Hodograph等性质。不同的是，贝塞尔曲线天然具备高阶连续性，且不必定义在固定区间[0,1]上。这给轨迹表征带来了很大的方便。

另外一个优点是B样条曲线能够进行局部调整，控制点调整所带来的影响是局部的，不会影响整条曲线的变化。

3. 非均匀有理B样条（Non-Uniform Ratioinal B-splines）

3.1 非均匀

显然地，节点间隔不均匀的B样条曲线就是非均匀B样条曲线（待补充）

3.2 有理