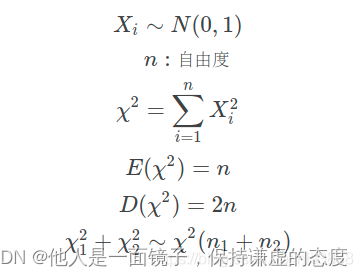理论:(1)卡方分布、非中心卡方分布详解 (概念、求阈值方法、非中心化参数求解办法等)

//======================================================================//

GNSS/INS紧组合导航系统完好性监测（理论和c++代码）专栏，后续会开源全部代码

https://blog.csdn.net/hltt3838/category_12207970.html?spm=1001.2014.3001.5482

//======================================================================//

目录

一、相关概念

1、卡方分布

2、卡方分布计算方法：

3、非中心卡方分布

二、卡方分布在组合导航故障检测中的作用

1、举例：

 2、非中心化参数求解

（1）求卡方分布的检测阈值

 （2）求非中心化参数（C++环境编译，亲测有效）

一、相关概念

1、卡方分布

若n个 相互独立 的随机变量 ξ₁、ξ₂、……、ξn ，均服从 标准正态分布N（0,1），则这n个服从标准正态分布的随机变量的 平方和 构成一新的随机变量，其分布规律称为卡方分布（chi-squaredistribution）；其中参数n称为自由度（通俗讲，样本中独立或能自由变化的自变量的个数，称为自由度），正如正态分布中均值或方差不同就是另一个正态分布一样，自由度不同就是另一个分布；其表达如下：

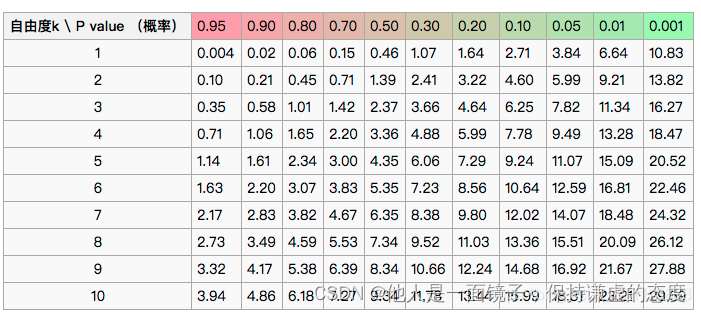
 概率密度函数和卡方分布表如下：

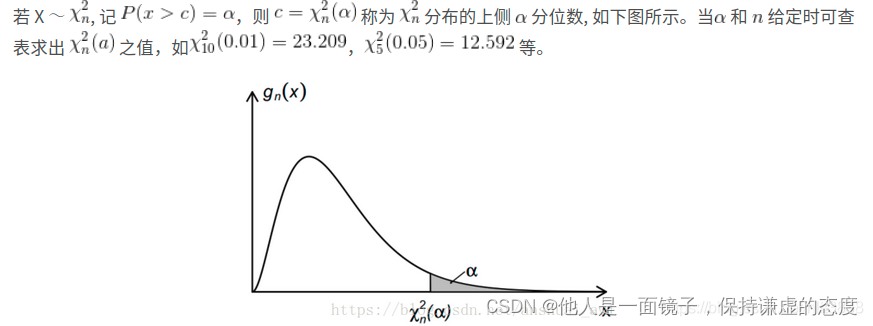
下表即为卡方分布表，第一列为自由度 (n)，第一行为显著水平 (α)，据此可以查找到临界值，如果检验统计量大于临界值，则检验统计量就位于拒绝域以内，说明观察结果与期望结果之间的差异显著 （也是完好性判断的本质）

•  什么是显著水平 ？（其实就是 误警率）

 

2、卡方分布计算方法：

• 卡方分布在线计算网址：

Chi Square Calculator - ChiSquareTable.net

• 也可以用pyhon写程序，代码如下：

from scipy.stats import norm
from scipy.stats.distributions import chi2
from scipy.stats import ncx2

# 完好性风险相关：(风险概率,均值, 方差)
ppf_1 = norm.ppf(q=0.99999, loc=0, scale=1)  
print(ppf_1)

# 卡方分布相关：(1-P_FA, 自由度)

ppf_2 = chi2.ppf(0.99999, df=3)  
print(ppf_2)         

            

# 非中心参数相关：(1-P_MD, 自由度，非中心化参数)

ppf_3 = ncx2.ppf(0.999, 3, 2.785)  
print(ppf_3)          

•  也可以用MATLAB 语句

chi2inv(1-P_FA, 自由度)

3、非中心卡方分布

二、卡方分布在组合导航故障检测中的作用

1、举例：

理解：卡方分布在第一象限内，卡方值都是正值，呈正偏态（右偏态），随着参数 n 的增大；卡方分布趋近于正态分布；随着自由度n的增大，卡方分布向正无穷方向延伸（因为均值n越来越大），分布曲线也越来越低阔（因为方差2n越来越大）概率是概率密度函数的区间积分！

 

 2、非中心化参数求解

（1）求卡方分布的检测阈值

 （2）求非中心化参数（C++环境编译，亲测有效）

 sn：自由度、T检测阈值、0.00001：漏检概率

#include <boost/math/distributions/non_central_chi_squared.hpp>

double lam = boost::math::non_central_chi_squared_distribution<double>::find_non_centrality(sn, T, 1 - 0.00001);