数学建模时序数据分析——趋势性检验和平稳性检验_先趋势还是平稳

数学建模数据分析——趋势性检验和平稳性检验

在数学建模比赛中，经常需要对数据进行分析和预处理，常见的比如趋势分析（上升/下降/无明显趋势）和突变分析，很多时候靠人的经验观察得出结论，但这是不够严谨的。于是我们通常会采用一些更科学的方法，下面我们就来详细的捋一遍数据分析检验方法：

时间序列趋势性检验方法

斜率法

原理

斜率法就是使用最小二乘法对时序数据进行拟合，根据拟合的直线的斜率K来判断序列的数据走势，当K>0时，则代表上升趋势；当k<0时，则代表下降趋势；

优缺点

优点为使用简单；缺点是要求数据是线性的，当数据波动较大时无法准确拟合，导致丧失了评价意义。

Cox-Stuart检验法

原理

直接考虑数据的变化趋势，若数据呈现上升趋势，则排在后面的数据的值要比排在前面的数据的值显著的大；反之，若数据呈现下降趋势，则排在后面的数据的值要比排在前面的数据的值显著的小。该方法利用前后两个时期不同数据的差值的正负来判断数据的总的变化趋势。

算法步骤

1. 取$x_i$和$x_i+c$组成一对$(xi,xi+c)$。这里如果$n$为偶数，则$c=n/2$，如果$n$是奇数，则$c=(n+1)/2$。当n为偶数时，共有$n’=c$对，而$n$是奇数时，共有$n’=c-1$对。
2. 用每一对的两元素差$D_i=x_i-x_{i+c}$的符号来衡量增减。令$S_{+}$为正的$D_i$的数目，$S_{-}$为负的$D_i$的数目。显然当正号太对时有下降趋势，反之有增长趋势。在没有趋势的零假设下他们因服从二项分布$B(n’,0.5)$。
3. 用$p(+)$表示取到正数的概率，用$p(-)$表示取到负数的概率，这样就得到符号检验方法来检验序列是否存在趋势性。

优缺点

优点是不依赖趋势结构，可以快速判断趋势是否存在；缺点是未考虑数据的时序性，仅从符号检验来判断

实现代码

假设有下面一个时序数据，波动性较大，无法根据经验判断数据呈上升还是下降趋势。

import matplotlib.pyplot as plt

a_array = [206,223,235,264,229,217,188,204,182,230,223,227,242,238,207,208,
           216,233,233,274,234,227,221,214,226,228,235,237,243,240,231,210]

plt.plot(range(1, len(a_array) + 1), a_array)
1
2
3
4
5
6

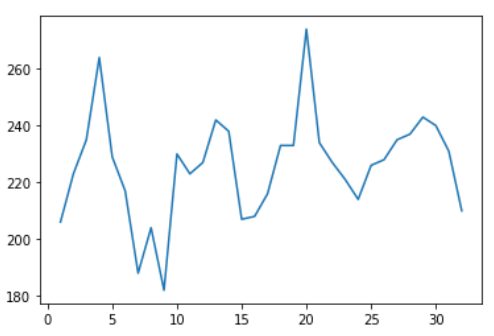
统计正的$D_i$出现次数为14次，负的$D_i$出现次数为2次，接下来判断是否存在显著的上升趋势

做出原假设$H_0$：该数据不存在上升趋势；

做出替代假设$H_1$：该数据存在上升趋势。

运行CS趋势检验方法，可以发现，使用二项式离散分布检验得到p-value值为0.004181，小于0.05，因此有理由认为原假设$H_0$不成立，从而支持假设$H_1$：该数据存在上升趋势

import numpy as np
import pandas as pd
import scipy.stats as stats

def cox_staut(list_c):
    lst=list_c.copy() ## 副本
    n0 = len(lst) ##列表长度
    
    ## 判断奇偶性
    if n0%2 == 1:
        del lst[int((n0-1)/2)] #奇数删除中间数值
        
    ## 配对前后数据
    c=int(len(lst)/2)
    ## 统计正Di和负Di出现次数
    pos=neg=0
    for i in range(c):
        diff=lst[i+c]-lst[i]
        if diff>0:
            pos+=1
        elif diff<0:
            neg+=1
        else:
            continue
    
    n1=pos+neg
    k=min(pos,neg)
    ## 使用二项式离散分布检验趋势是否显著
    p=2*stats.binom.cdf(k,n1,0.5)
    print('fall:%i  rise:%i  p-value:%f'%(neg, pos, p))

cox_staut(a_array)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

fall:2  rise:14  p-value:0.004181
1

Mann-Kendall检验法

原理
Mann-Kendall检验不需要样本遵循一定的分布，也不受少数异常值的干扰。在Mann-Kendall检验中，原假设$H_0$为时间序列数据$(X1，\dots ,Xn)$,是$n$个独立的、随机变量同分布的样本；备择假设$H_1$ 是双边检验，对于所有的$k，j\le n$，且$k\ne j$，$X_k$和$X_j$的分布是不相同的。若原假设是不可接受的，即在α置信水平上，时间序列数据存在明显的上升或下降趋势。对于统计量$Z$，大于0时是上升趋势；小于0时是下降趋势。

算法步骤

1. 将数据按采集时间列出：$x_1,x_2,\dots ,x_n$，即分别在时间$1,2,\dots ,n$得到的数据。

2. 确定所有$n(n-1)/2$个$xj-xk$差值的符号，其中$j>k$，，这些差值是：$x_2-x_1，x_3-x_1,\dots ,x_n-x_1，x_3-x_2，x_4-x_2，\dots ，x_n-x_{n-2}，x_n-x_{n-1}$

3. 令$sgn(x_j-x_k)$作为指示函数，依据$x_j-x_k$的正负号取值为1,0或-1，即
   s g n ( x j − x k ) = { 1 , x j − x k > 0 − 1 , x j − x k < 0 0. x j − x k = 0 sgn(x_j-x_k)=

   $$\begin{cases} 1, x_j − x_k > 0\\ -1, x_j − x_k < 0\\ 0. x_j − x_k = 0 \end{cases}$$ sgn(xj​−xk​)=⎩⎪⎨⎪⎧​1,xj​−xk​>0−1,xj​−xk​<00.xj​−xk​=0​

4. 计算$S={\sum }_{k-1}^{n-1}{\sum }_{j-k+1}^{n}sgn(x_j-x_k)$。即差值为正的数量减去差值为负的数量。如果$S$是一个正数，那么后一部分的观测值相比之前的观测值会趋向于变大；如果S是一个负数，那么后一部分的观测值相比之前的观测值会趋向于变小。

5. 如果$n\le 10$，依据Gilbert (1987, page 209, Section 16.4.1)中所描述的程序，接下来要在概率表 (Gilbert 1987, Table A18, page 272) 中查找$S$。如果此概率小于$\alpha$(认为没有趋势时的截止概率)，那就拒绝零假设，认为趋势存在。如果在概率表中找不到n(存在结数据——tied data values——会发生此情况)，就用表中远离0的下一个值。比如$S=12$，如果概率表中没有$S=12$，那么就用$S=13$来处理也是一样的。
   如果$n>10$，则依以下步骤6-10来判断有无趋势。这里遵循的是Gilbert (1987, page 211, Section 16.4.2)中的程序。

6. 计算S的方差如下：$VAR(S)=\frac{1}{18}[n(n-1)(2n+5)-{\sum }_{p-1}^g{t}_p(t_p-1)(2t_p+5)]$。其中$g$是结组（tied groups）的数量，$t_p$是第p组的观测值的数量。例如：在观测值的时间序列$23,24,29,6,29,24,24,29,23$中有$g=3$个结组，相应地，对于结值(tiied value)23有$t_1=2$、结值24有$t_2=3$、结值29有$t_3=3$。当因为有相等值或未检测到而出现结时，$VAR(S)$可以通过Helsel (2005, p. 191)中的结修正方法来调整。

7. 计算MK检验统计量Z_{MK}:
   Z M K = { S − 1 V A R ( S ) , S > 0 0 , S = 0 S + 1 V A R ( S ) , S > 0 Z_{MK}=

   $$\begin{cases} \frac{S-1}{\sqrt{VAR(S)}},& S>0\\ \qquad0\quad,& S=0\\ \frac{S+1}{\sqrt{VAR(S)}},& S>0 \end{cases}$$ ZMK​=⎩⎪⎪⎨⎪⎪⎧​VAR(S) ​S−1​,0,VAR(S) ​S+1​,​S>0S=0S>0​
   设想要测试零假设。$H_0$(没有单调趋势)对比替代假设Ha(有单调增趋势)，其1型错误率为α，0<α<0.50（注意α是MK检验错误地拒绝了零假设时可容忍的概率——即MK检验拒绝了零假设是错误地，但这个事情发生概率是α，我们可以容忍这个错误）。如果$Z_{MK}\ge Z_1-\alpha$，就拒绝零假设H0，接受替代假设$H_a$，其中$Z_1-\alpha$是标准正态分布的100(1−α)th百分位。

8. 测试上面的H0与Ha（有单调递减趋势），其1型错误率为alpha，0<α<0.5，如果ZZMK≤–Z1−α，就拒绝零假设H0，接受替代假设Ha

9. 测试上面的H0与Ha（有单调递增或递减趋势），其1型错误率为alpha，0<α<0.5，如果|ZMK|≥Z1−α2，就拒绝零假设H0，接受替代假设Ha，其中竖线代表绝对值。

实现代码

笔者自己找了一个时序数据，长度为2000，由于数据较长，就不再展示了。由时序图可以看出该数据波动性较大，无法根据经验判断数据呈上升还是下降趋势。

plt.plot(range(1, len(b_array) + 1), b_array)
1

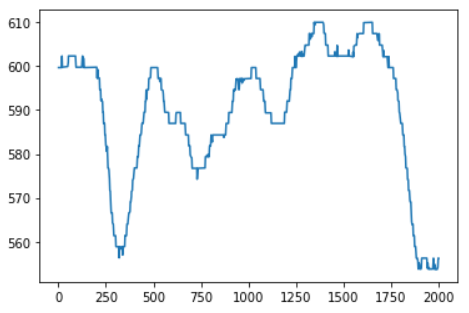
根据上述提供的思路，做出假设，并判断数据的变化趋势。

运行MK趋势检验方法，可以发现，P-value值为4.10e-12，小于给定的显著性水平，因此有理由认为该时序数据呈现上升趋势。

import math
from scipy.stats import norm, mstats
import numpy as np

def mk_test(x, alpha=0.05):
    n = len(x)

    # calculate S
    s = 0
    for k in range(n-1):
        for j in range(k+1, n):
            s += np.sign(x[j] - x[k])

    # calculate the unique data
    unique_x, tp = np.unique(x, return_counts=True)
    g = len(unique_x)

    # calculate the var(s)
    if n == g:  # there is no tie
        var_s = (n*(n-1)*(2*n+5))/18
    else:  # there are some ties in data
        var_s = (n*(n-1)*(2*n+5) - np.sum(tp*(tp-1)*(2*tp+5)))/18

    if s > 0:
        z = (s - 1)/np.sqrt(var_s)
    elif s < 0:
        z = (s + 1)/np.sqrt(var_s)
    else: # s == 0:
        z = 0

    # calculate the p_value
    p = 2*(1-norm.cdf(abs(z)))  # two tail test
    h = abs(z) > norm.ppf(1-alpha/2)

    if (z < 0) and h:
        trend = 'decreasing'
    elif (z > 0) and h:
        trend = 'increasing'
    else:
        trend = 'no trend'

    return trend, p, h

mk_test(b_array)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

('increasing', 4.100275674545628e-12, True)
1

时间序列平稳性检验方法

平稳时间序列定义与性质

平稳时间序列按照限定条件的严格程度可以分为以下两种类型：

严平稳时间序列：严平稳顾名思义，是一种条件非常苛刻的平稳性，它要求序列随着时间的推移，其统计性质保持不变。

设 { X t } \{X_t\} {Xt​}为一时间序列，对任意的正整数$m$，任取$t_1,t_2,\cdots ,t_m\in T$，对任意整数$\tau$，其联合概率密度函数满足：

$$F_{t_1,t_2,\cdots ,t_m}(x_1,x_2,\cdots ,x_m)=F_{t_{1+\tau },t_{2+\tau },\cdots ,t_{m+\tau }}(x_1,x_2,\cdots ,x_m)$$
则称时间序列 { X t } \{X_t\} {Xt​}为严平稳时间序列。严平稳的条件只是理论上的存在，现实中用得比较多的是宽平稳的条件。

宽平稳时间序列：宽平稳也叫弱平稳或者二阶平稳（均值和方差平稳），满足：

1. 均值为常数，即
   $$E(X_t)=u,\forall t\in T$$

2. 方差为常数
   $$D(X_t)=\gamma (t,t)=\gamma (0),\forall t\in T$$

3. 自协方差为常数，即自协方差函数和自相关系数只依赖于时间的平移长度，而与时间的起点无关。
   $$\gamma (t,s)=\gamma (k,k+s-t),\forall t,s,k\in T$$
   因此，可以记$\gamma (k)$为时间序列 { X t } \{X_t\} {Xt​}的延迟$k$自协方差函数。

在现实生活中，时间序列是很难满足严平稳时间序列的要求的，因此，一般所讲的平稳时间序列在默认情况下都是指宽平稳时间序列。

由于平稳时间序列具有这些优良性质，因此，对于一个平稳时间序列来说，其待估计的参数量就变得少了很多，因为他们的均值、方差都是一样的，因此，可以利用全部的样本来估计总体的均值和方差，即：
$$\begin{gathered} \hat{\mu }=\bar{x}=\frac{{\sum }_{i=1}^{n}x}{n} \\ \hat{\gamma }(0)=\frac{{\sum }_{t-1}^n(x_t-\bar{x}{)}^2}{n-1} \end{gathered}$$
所以当拿到一个时间序列后，需要对其进行平稳性检验。

检验方法

平稳性检验的主要方法是看时序图、ACF图和单位根检验，其中单位根检验方法有ADF、PP、KPSS等。其中ADF和PP检验都拒绝原假设，即认为序列平稳；KPSS拒绝原假设，即认为序列非平稳（KPSS零假设和ADF/PP恰好相反）。当出现不一致时，需要根据属于下面哪种平稳过程来判断，有一种观点认为KPSS检验结果更强更鲁棒，因为ADF和PP检验将差分平稳模型作为零假设，它检验随机游走或带漂移的随机游走效果奇好，但它们都需要假设是否包含常数均值和时间趋势，因此拒绝零假设的功效（low power）较低，而KPSS则完全不需要选择假设类型。

时序图检验法

那么，当拿到一个时间序列后，应该如何对其进行平稳性的检验呢？目前，对时间序列的平稳性检验主要有两种方法，一种是图检法，即根据时序图和自相关图进行直观判断，另一种是构造检验统计量的方法，目前主要有单位根检验法。
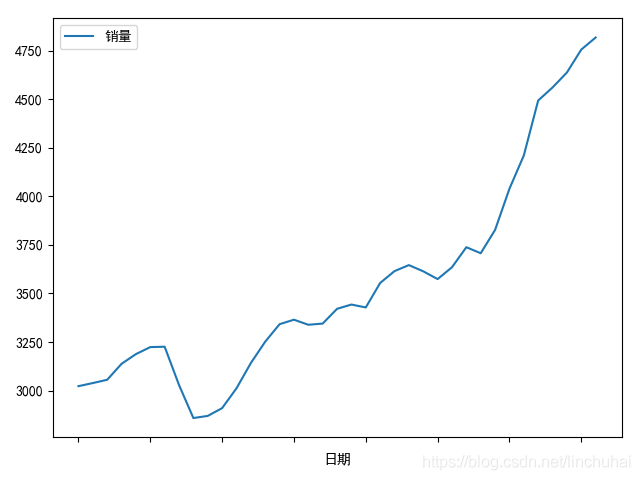
    对于图检法，我们一般绘制时间序列的时序图，如下图所示，如果时间序列是平稳的，那么序列应该是围绕某一个均值上下随机波动，而下图中的序列明显具有一定的增长趋势，因此，可以断定该序列肯定不是平稳时间序列。

自相关图检验法

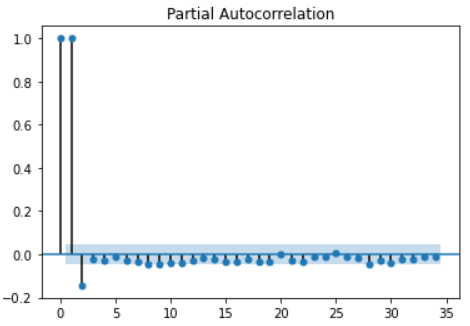
对于平稳时间序列，其自相关图一般随着阶数的递增，自相关系统会迅速衰减至0附近，而非平稳时间序列则可能存在先减后增或者周期性波动等变动。如下图所示，该时间序列随着阶数的递增，自相关系数始终在$[0.8,1]$之间，衰减微弱，因此，可以判断该时间序列不是平稳时间序列。

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

plot_acf(b_array)
plot_pacf(b_array)
1
2
3
4

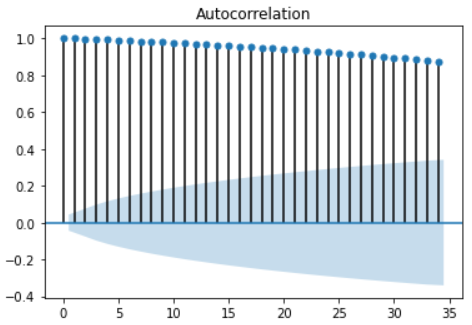
除了上述两种方法，便是单位根检验，下面这张图对单位根检验做了很好地说明。

ADF检验法

在使用很多时间序列模型的时候，如 ARMA、ARIMA，都会要求时间序列是平稳的，所以一般在研究一段时间序列的时候，第一步都需要进行平稳性检验，除了用肉眼检测的方法，另外比较常用的严格的统计检验方法就是ADF检验，也叫做单位根检验。

ADF检验全称是 Augmented Dickey-Fuller test，顾名思义，ADF是 Dickey-Fuller检验的增广形式。DF检验只能应用于一阶情况，当序列存在高阶的滞后相关时，可以使用ADF检验，所以说ADF是对DF检验的扩展。
原理

ADF检验就是判断序列是否存在单位根：如果序列平稳，就不存在单位根；否则，就会存在单位根。

所以，ADF检验做出的假设为：

**原假设$H_0$