- 1next 14 appRouter redux数据持久化_nextjs redux 持久化存储
- 2mac与windows服务器 访问和共享
- 3Android 15全面解读:性能飙升、隐私守护与智能生活新纪元_安卓15
- 4标题:怎样通过Dialogflow构建一个聊天机器人?React版。_dialogflow机器人
- 5连接Mongodb数据库的步骤以及注意事项_如何连接mongodb数据库
- 6小程序公告php实现,小程序两种滚动公告栏的实现方法
- 7Git仓库完整迁移全过程_gitee 将a仓库的克隆到b仓库
- 8FP6381AS5CTR原厂SOT23-5 1.2A同步降压IC DC-DC变频器
- 9STM32参考代码,编译时出现“cannot open source input file, no such file or directory"错误
- 10微信小程序用户隐私保护指引设置指南_mp后台-设置-基本设置-服务内容声明-用户隐私保护指引]中声明“剪切板”隐私收集
【数据结构】树(二)—— 二叉树(C语言版)_二叉树c语言
赞
踩
一、二叉树的定义
二叉树(Binary Tree)是n(n≥0)个结点的有限集合, 该集合或者为空集(称为空二叉树),或者由一个根节点和两棵互不相交的、分别称为根节点的左子树和右子树的二叉树组成。
二、二叉树的特点
1. 特点
每个结点最多有两棵子树,故不存在度大于2的结点;
左子树和右子树是有顺序的,次序不能任意颠倒;
即使树中某结点只有一棵子树,也要区分是左子树还是右子树;
- 1
- 2
- 3
2. 五种基本形态
空二叉树;
只有一个根节点;
根节点只有左子树;
根节点只有右子树;
根节点既有左子树又有右子树;
- 1
- 2
- 3
- 4
- 5
三、特殊二叉树
1. 斜树
斜树:所有结点都只有左子树的二叉树叫左斜树,对应有右斜树,统称为斜树;
2. 满二叉树
满二叉树:所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上的二叉树;
叶子只能出现在最下一层,否则不平衡;
非叶子节点的度一定是2;
同样深度的二叉树,满二叉树的结点个数最多,叶子数最多;
- 1
- 2
- 3

3. 完全二叉树
完全二叉树:对一棵具有n个结点的二叉树按层序编号,如果编号为i(1≤i≤n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这棵二叉树称为完全二叉树
叶子结点只能出现在最下两层
最下层的叶子一定集中在左部连续位置
倒数二层,若有叶子结点,一定都在右部连续位置
如果结点度为1,则该结点只有左孩子,即不存在只有右子树的情况
同样结点数的二叉树,完全二叉树的深度最小
- 1
- 2
- 3
- 4
- 5

注:满二叉树一定是完全二插树,但完全二插树不一定是满的。
四、二叉树的性质
(1)在二叉树的第 i 层上至多有2i−1个结点(i≥1)
(2)深度为 k 的二叉树至多有2k−1个结点(k≥1)
(3)对任何一棵二叉树T, 如果其终端结点数为n0, 度为2的结点树为n2, 则n0=n2+1
(4)具有n个结点的完全二叉树的深度为 [ log2n ] + 1( [ x ]表示不大于x的最大整数)
(5)如果对一棵具有n个结点的完全二叉树 (其深度为 ⌊log2n⌋+1) 的结点按层序编号(从第1层到第⌊log2n⌋+1层,每层从左到右),对任一结 i (1≤i≤n)有:
- 如果 i = 1, 则结点i是二叉树的根,无双亲;
- 如果 i > 1, 则其双亲是结点⌊i/2⌋;
- 如果 2i > n, 则结点 i 无左孩子(结点 i 为叶子结点); 否则即 2i ≤ n 时其左孩子是结点 2i;
- 如果 2i+1 > n, 则结点 i 无右孩子;否则 2i+1≤ n 时, 其右孩子是结点2i+1;
五、二叉树的存储结构
1. 二叉树顺序存储结构
二叉树是一种特殊的树,由于他的特殊性,使得用顺序存储结构也可以实现。
顺序存储结构一般只用于 完全二叉树,否则会造成空间浪费
二叉树的顺序存储结构就是利用一维数组存储二叉树中的结点, 并且结点的存储位置,也就是数组的下标要能体现结点之间的逻辑关系,比如双亲与孩子之间的关系。

将这棵二叉树存入数组中,相应的下标存入其相同位置结点的数据

对于一般二叉树,可以将其按照完全二叉树进行编号,用一维数组存储,对于不存在的结点设置为“null”。

极端情况:
一棵深度为 k 的右斜树,它只有 k 个结点, 却需要分配 2k - 1 个存储单元空间,对存储空间浪费极大。 故而顺序存储结构只适用于完全二叉树。

#include<stdio.h>
#include<conio.h>
#define MAX_SIZE 1024
typedef char TElemType;
//定义顺序树类型
typedef TElemType SeqTree[MAX_SIZE];
// 定义了一个数据类型 SeqBiTree , 是一个数组类型,每一个变量包含元素类型为 TElemType,个数为MAX_TREE_SIZE
void InitSeqTree(SeqTree tree)/* 构造空二叉树T。因为T是固定数组,不会改变,故不需要& */
{
//将字符数组中的所有元素初始化赋值
for(int i = 0 ; i < MAX_SIZE ; i++ )
{
tree[i] = '\0';
}
}
// 前序遍历,实现二叉树的顺序存储
void CreatSeqTree(SeqTree tree, int i )
{
char ch;
ch = getchar();
fflush(stdin); //清空键盘缓存区
tree[0] = '\0';
//int i = 1; // 设置根结点的位置序号与数组下标为1
if(ch == '^') //当输入^时结束节点输入
{
tree[i] = '\0';
return;
}
tree[i] = ch;
//建立完节点提示输入左子树和右子树
printf("请输入左子树:\n");
CreatSeqTree(tree , 2 * i );
printf("请输入右子树:\n");
CreatSeqTree(tree , 2 * i + 1);
}
//获得树的根节点
TElemType GetSeqTreeRoot(SeqTree tree)
{
return tree[1];
}
//获取节点总数
int GetSeqTreeLength(SeqTree tree)
{
int len = 0;
for(int i = 0 ; i < MAX_SIZE ; i++)
{
if(tree[i] == '\0'){
continue;
}
len++;
}
return len;
}
//获取深度 深度为k的二叉树最多有2^k - 1个节点
int GetSeqTreeDepth(SeqTree tree)
{
int depth = 0;
int len = GetSeqTreeLength(tree);
while((int)pow(2,depth) - 1 < len)
{
depth++;
}
return depth;
}
void PrintSeqTree(SeqTree tree)
{
for(int i = 0 ; i < MAX_SIZE ; i++)
{
printf("%c",tree[i]);
}
}
void main()
{
SeqTree tree;
InitSeqTree(tree);
printf("请输入根节点内容:");
CreatSeqTree(tree, 1);
PrintSeqTree(tree);
printf("\n");
printf("树的结点总数:%d\n",GetSeqTreeLength(tree));
printf("树的深度:%d\n",GetSeqTreeDepth(tree));
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
https://blog.csdn.net/rex_wust/article/details/84891522
#include<stdio.h>
#include<conio.h>
#define MAX_SIZE 1024
#define OK 1
#define ERROr 0
typedef int Status;
typedef char TElemType;
//定义顺序树类型
typedef TElemType SeqTree[MAX_SIZE];
void InitSeqTree(SeqTree tree)
{
for(int i = 0 ; i < MAX_SIZE ; i++ )//将字符数组中的所有元素初始化赋值
{
tree[i] = '\0';
}
}
// 前序遍历,实现二叉树的顺序存储
void CreatSeqTree(SeqTree tree, int i )
{
char ch;
ch = getchar();
fflush(stdin); //清空键盘缓存区
tree[0] = '\0';
//int i = 1; // 设置根结点的位置序号与数组下标为1
if(ch == '#') //当输入^时结束节点输入
{
tree[i] = '\0';
return;
}
tree[i] = ch;
//建立完节点提示输入左子树和右子树
printf("请输入左子树:\n");
CreatSeqTree(tree , 2 * i );
printf("请输入右子树:\n");
CreatSeqTree(tree , 2 * i + 1);
}
//获得树的根节点
TElemType GetSeqTreeRoot(SeqTree tree)
{
return tree[1];
}
//获取节点总数
int GetSeqTreeLength(SeqTree tree)
{
int len = 0;
for(int i = 0 ; i < MAX_SIZE ; i++)
{
if(tree[i] == '\0'){
continue;
}
len++;
}
return len;
}
//获取深度 深度为k的二叉树最多有2^k - 1个节点
int GetSeqTreeDepth(SeqTree tree)
{
int depth = 0;
int len = GetSeqTreeLength(tree);
while((int)pow(2,depth) - 1 < len)
{
depth++;
}
return depth;
}
int IsSeqTreeEmpty(SeqTree tree)
{
if (tree[1] == '\0')
return 1;
else
return 0;
}
void Visit (TElemType elem)
{
printf("%c", elem);
}
void PreTraverse(SeqTree tree, int i)
{
Visit(tree[i]);
if (tree[2*i] != '\0') // 左子树不为空
PreTraverse(tree, 2*i );
if (tree[2*i + 1] != '\0') // 右子树不为空
PreTraverse(tree, 2*i + 1);
}
Status PreOrderTraverse(SeqTree T)
{
if(IsSeqTreeEmpty(T) == 0) // 树不空
PreTraverse(T,1);
printf("\n");
return OK;
}
/*
int ParentLocate (SeqTree Tree, TElemType elem)
{
if(Tree[1] == '/0')
{
printf("这是一棵空树!");
return;
}
for (int i = 1; 1<= MAX_SIZE; i++)
{
if (Tree[i] == elem)
return i/2;
}
return 0;
}
TElemType PrintNode (SeqTree T, int i )
{
return T[i];
}
int LChildLocate (SeqTree Tree, TElemType elem)
{
if(Tree[1] == '/0')
{
printf("这是一棵空树!");
return;
}
for (int i = 1; 1<= MAX_SIZE; i++)
{
if (Tree[i] == elem)
return i*2;
}
return 0;
}
*/
int main()
{
SeqTree tree;
InitSeqTree(tree);
printf("请输入根节点内容:");
CreatSeqTree(tree, 1);
//PrintSeqTree(tree);
printf("\n");
printf("树的结点总数:%d\n",GetSeqTreeLength(tree));
printf("树的深度:%d\n",GetSeqTreeDepth(tree));
PreOrderTraverse(tree);
/*
TElemType elem;
scanf("%c", &elem);
printf("elem 的 双亲结点在数组元素中的下标:%d\n", ParentLocate(tree,elem));
printf("elem 的 双亲结点的数据域:%c", PrintNode(tree, ParentLocate(tree,elem)));
*/
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
- 111
- 112
- 113
- 114
- 115
- 116
- 117
- 118
- 119
- 120
- 121
- 122
- 123
- 124
- 125
- 126
- 127
- 128
- 129
- 130
- 131
- 132
- 133
- 134
- 135
- 136
- 137
- 138
- 139
- 140
- 141
- 142
- 143
- 144
- 145
- 146
- 147
- 148
- 149
- 150
- 151
- 152
- 153
- 154
- 155
- 156
- 157
- 158
- 159
- 160
- 161
- 162
- 163
- 164
- 165
- 166
- 167
- 168
- 169
- 170
- 171
- 172
- 173
- 174
- 175
- 176
- 177
- 178
2. 二叉链表(链式存储结构)
二叉树每个结点最多有两个孩子,故结点结构为一个数据域和两个指针域

其中 data 是数据域, lchild 和 rchild 都是指针域, 分别存放指向左孩子和右孩子的指针。
/* 二叉树的二叉链表结点结构定义 */
typedef struct BiTNode
{
TElemType data; // 结点数据
struct BiTNode *lchild, *rchild; // 左右孩子指针
}BiTNode, *BiTree;
- 1
- 2
- 3
- 4
- 5
- 6

注: 为了便于找到结点的双亲,可以添加一个增加指向结点双亲的指针域。
六、遍历二叉树
二叉树的遍历(traversing binary tree)是指从根节点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且仅被访问一次。
二叉树的层次遍历属于广度优先遍历;二叉树的前、中、后序遍历属于深度优先遍历
1. 前序遍历
规则是若二叉树为空,则空操作返回,否则先返回根节点,然后前序遍历左子树,再前序遍历右子树。
下图遍历顺序为: ABDGHCEIF

递归版
void PreOrderTraverse(BiTree T) // 由上例结构体定义,BiTree 为指向二叉树的指针
{
if(T == NULL)
return;
printf("%c", T->data);
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
非递归版
思想: 由前序遍历顺序可知,首先访问根节点,然后分别访问左子树和右子树。对于每个子树来说,以同样的顺序进行
步骤
- 访问结点 p, 然后将其入栈;
- 判断结点p的左子树是否为空,若不为空,将p左子树作为当前的结点p 。若为空,则取出栈顶结点并进行出栈操作,并将栈顶结点的右子树作为当前结点p;
- 知道p为NULL并且栈为空,遍历结束
void PreOrderTraverseNoRecursive(BiTree T)
{
stack<BiTree> s;
BiTree p = T;
while(p != NULL || !s.empty())
{
while(p != NULL)
{
printf("%c", p->data);
s.push(p);
p = p->lchild;
}
if(!s.empty())
{
p = s.top();
s.pop();
p = p->rchild;
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
2. 中序遍历
规则是若树为空,则空操作返回,否则从根节点开始(注意并不是先访问根节点),中序遍历根节点的左子树,然后是访问根节点,最后中序遍历右子树。下图遍历顺序为:GDHBAEICF

#####递归版
void InOrderTraverse(BiTree T) // 由上例结构体定义,BiTree 为指向二叉树的指针
{
if(T == NULL)
return;
InOrderTraverse(T->lchild);
printf("%c", T->data);
InOrderTraverse(T->rchild);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
非递归版
思想:按中序遍历顺序,先访问左子树,再访问根节点,后访问右子树。对于每个子树来说,按同样顺序进行遍历。
步骤
若当前结点p的左子树不为空,则将p入栈,并将p左子树置为当前节点,按相同规则进行
若当前结点左子树为空,则取出栈顶元素并进行出栈操作,访问该栈顶结点,将当前结点p置为该栈顶结点的右子树
知道p为NULL并且栈为空遍历结束
- 1
- 2
- 3
void InOrderTraverseNoRecursive(BiTree T)
{
stack<BiTree> s;
BiTree p = T;
while(p != NULL || !s.empty())
{
while(p != NULL)
{
s.push(p);
p = p->lchild;
}
if(!s.empty())
{
p = s.top();
s.pop();
printf("%c", p->data);
p = p->rchild;
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
3. 后序遍历
规则是若树为空,则空操作返回,否则从左到右先叶子后结点的方式遍历访问左右子树,最后是访问根节点。下图遍历顺序为:GHDBIEFCA

递归版
void PostOrderTraverse(BiTree T) // 由上例结构体定义,BiTree 为指向二叉树的指针
{
if(T == NULL)
return;
PostOrderTraverse(T->lchild);
PostOrderTraverse(T->rchild);
printf("%c", T->data);
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
非递归版
思想:后序遍历的非递归版本比较复杂,使用一个栈的话,过程比较繁琐。此处选择使用两个栈。
步骤
将当前节点p入栈一s
将栈一栈顶元素出栈,并入栈st
然后将当前结点的左子树和右子树入栈一s
按相同顺序进行,直到栈s为空
最后,所有结点已经入栈st,且按照后序遍历的顺序存放,直接全部出栈,访问结点即可
- 1
- 2
- 3
- 4
- 5
void PostOrderTraverseNoRecursive(BiTree T)
{
if(!T)
return;
stack<BiTree> s, st;
BiTree p;
s.push(T);
while(!s.empty())
{
p = s.top();
st.push(p);
s.pop();
if(p->lchild)
s.push(p->lchild);
if(p->rchild)
s.push(p->rchild);
}
while(!st.empty())
{
printf("%c", st.top()->data);
s.pop();
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
4. 层序遍历
规则是若树为空,则空操作返回,否则从树的第一层,也就是根节点开始访问,从上而下逐层遍历,在同一层中,按从左到右的顺序对结点逐个访问。下图遍历顺序为:ABCDEFGHI

思想:层序遍历由于层级的关系,需要使用队列存储,从左到右,从上到下。依次将该结点,该结点的左子树,该结点的右子树入队,即可保证顺序是层序排列。
步骤
若根节点不为空,则将根节点入队,进入循环
将首元素出队,并且访问该结点
如果该结点有左孩子,将其左孩子入队
如果该结点有右孩子,将其右孩子入队
- 1
- 2
- 3
- 4
/* 二叉树的层序遍历算法 */
void LevelOrderTraverse(BiTree T)
{
if(T == NULL)
return;
queue<BiTree> q;
BiTree p;
q.push(T);
while(!q.empty())
{
p = q.front();
printf("%c", p->data);
q.pop();
if(p->lchild)
q.push(p->lchild);
if(p->rchild)
q.push(p->rchild);
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
二叉树遍历推导遍历结果分析
1. 单个遍历序列无法确定唯一二叉树
一个前序遍历序列可能对应多种二叉树形态;

一个中序遍历序列可能对应多种二叉树形态;

同理:一个后序遍历序列可能对应多种二叉树形态;
结论:若只给出一棵二叉树的 前序/中序/后序/层次 遍历序列中的一种,不能唯一确定一棵二叉树。
2. 遍历组合推导出唯一一棵二叉树
- 已知前序遍历序列和中序遍历序列,可以确定唯一的二叉树
- 已知后序遍历序列和中序遍历序列,可以确定唯一的二叉树
- 已知层次遍历序列和中序遍历序列,可以确定唯一的二叉树
思路:
(1)抓住前序遍历首结点为根结点;后序遍历的尾结点为根结点;
(2)由前序/后序遍历的首结点/尾结点确定根结点,再由中序遍历序列划分左右子树,依次进行递归操作;
对于层次遍历序列,由层次遍历的特点可知,首结点为根结点,由中序遍历序列划分左右子树,再由层次遍历序列确定左右子树的根结点
举例;
层次遍历序列:ABCDE
中序遍历序列:ACBED
- 1
- 2
(1)由层次遍历序列知 A 为树的根结点;
(2)由中序遍历序列知,A 为树的根结点时,只有右子树;再由层次遍历序列其他结点位置可知,B 结点为右子树的根结点;
(3)在由层次遍历序列,根据B 结点为右子树根结点,划分出左子树 C,和右子树 ED;
(4)在有层次遍历序列的性质知,C、D 分别为以 B 为结点的左右子树的根结点。
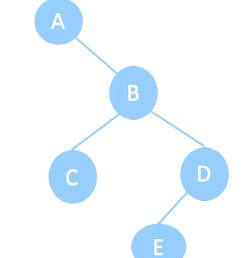
七、树和森林的遍历
1. 树的遍历
先根遍历,先访问树的根结点,然后依次访问每棵子树,从左到右遍历其余的子树 。
后根遍历, 遍历第一颗子树 ,从左到右遍历其余的子树,最后访问根节点 。
- 1
- 2
根据树与二叉树的转换关系以及二叉树的遍历定义可以推知,当以二叉链式方式存储一颗一般树时,
(1)树的先序遍历与其转换的相应的二叉树的先序遍历的结果序列相同;
(2)树的后序遍历与其转换的二叉树的中序遍历的结果序列相同;
(3)树的层序遍历与其转换的二叉树的后序遍历的结果序列相同。
2. 森林的遍历
前序遍历,先访问第一棵树的根结点,然后依次先根遍历每一棵子树,然后下一课树。
后序遍历,先后根遍历第一棵树,然后下一课,然后下一棵。
- 1
- 2
由森林与二叉树的转换关系以及森林与二叉树的遍历定义可知,
(1)森林的先序遍历与所转换得到的二叉树的先序遍历的结果序列相同。
(2)森林的后序遍历与所转换得到的二叉树的中序遍历的结果序列相同。
一般树二叉链存储方式下层次遍历:
按层次遍历,那就肯定得用到队列;前序,后序,中序就得用到栈:
当一个节点被访问的同时,还要检查该节点有无左子树,如果非空即表示该节点有下一层,这颗左子树的根就是下一层节点中的最左孩子。将这颗左子树的根进队,然后,继续访问右单支所有节点,并对访问的节点做左子树检查和相应的操作。当一个右单支上的左右节点全部被访问后,就从队列中出队一个节点的指针,该指针正好是下一层中最左的一个节点。再从该出队节点开始,像右单支访问,并重复以上的整个过程。
八、二叉树的建立
/* 按前序输入二叉树中结点的值(一个字符), # 表示空树,构造二叉链表表示二叉树 T */
void CreateBiTree(BiTree &T)
{
TElemType ch;
scanf("%c", &ch);
if(ch == '#')
*T = NULL;
else
{
(*T) = (BiTree)malloc(sizeof(BiTNode));
if(!*T)
exit(OVERFLOW);
(*T)->data = ch; // 生成根节点
CreateBiTree(&(*T)->lchild); // 构造左子树
CreateBiTree(&(*T)->rchild); // 构造右子树
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
#include<stdlib.h>
#include<stdio.h>
#define OVERFLOW 0
#define NULL 0
typedef struct BitNode //二叉树结构,包含一个数据域,两个指针
{
char data;
struct BitNode *lchild, *rchild;
}BitNode, *BitTree;
void CreatBitTree(BitTree *T) //二叉树建立
{
char ch;
scanf("%c", &ch);
if(ch == '#')
*T = NULL;
else
{
*T = (BitTree)malloc(sizeof(BitNode));
if(!*T)
exit(OVERFLOW);
(*T)->data = ch;
CreatBitTree(&(*T)->lchild);
CreatBitTree(&(*T)->rchild);
}
}
void PreOrderTraverse(BitTree T) //二叉树前序遍历
{
if(T == NULL)
return;
printf("%c", T->data);
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
void InOrderTraverse(BitTree T) //中序遍历
{
if(T == NULL)
return;
InOrderTraverse(T->lchild);
printf("%c", T->data);
InOrderTraverse(T->rchild);
}
void PostOrderTraverse(BitTree T) //后序遍历
{
if(T == NULL)
return;
PostOrderTraverse(T->lchild);
PostOrderTraverse(T->rchild);
printf("%c", T->data);
}
int main()
{
BitTree T;
CreatBitTree(&T);
PreOrderTraverse(T);
printf("\n");
InOrderTraverse(T);
printf("\n");
PostOrderTraverse(T);
printf("\n");
return 0;
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70


