自主导航与路径规划无人机研究现状_路径规划研究现状

目录

 1.SLAM算法的研究现状

 2. 无人机定位研究现状

 3 路径规划的研究现状

参考文献

1.SLAM算法的研究现状

        移动机器人根据传感器获取的自身状态信息和环境信息构建环境地图的过程被称之为SLAM问题，SLAM问题能否解决是移动机器人自主定位以及路径规划的充分条件。1986年Smith等人[20]首先研究了SLAM的相关技术直到2021年经过了30多年的发展移动机器人的自主导航领域[21]中必不可少的科学技术。 在SLAM问题被提出的早期，研究人员普遍通过超声波传感器进行研究，随着传感器技术的多元化发展，解决SLAM问题的方案逐渐被2D/3D激光雷达、单目相机、双目相机和RGB-D相机所取代。随着传感器种类的不断增多，解决SLAM的方案也逐渐多样化发展。国内外的研究学者开始将多个传感器的测量数据相互融合，并将融合数据作为SLAM技术的输入。根据处理传感器数据的原理不同可以将SLAM算法分为滤波原理的SLAM算法和优化原理的SLAM算法[21]。分类结果如图1所示:

        1987年Smith等人[22]首先提出的基于卡尔曼滤波的SLAM算法算法，也奠定了基于滤波原理的SLAM方法。使用滤波原理的SLAM方法主要依靠Bayes状态估计理论，通过当前的测量值和观测值来估计系统的后验状态。又根据不同的求解后验概率的方法，又可以细致的分为基于扩展卡尔曼滤波(EKF)[23]、基于无迹卡尔曼滤波(UKF)、基于扩展信息滤波(EIF)和基于稀疏扩展信息滤波(SEIF)的SLAM方法[24]。EKF或UKF对于非线性的系统有着良好的估计速度和准确率。但是由于KF会产生高斯白噪声，导致SLAM定位和建图的准确度下降，并且由于在非结构化的空间中特征点数量非常大，导致基于滤波原理的SLAM的计算量急速增加[25]。

        为了解决基于KF的SLAM算法的计算量大、局限性强等缺点，Doucet等人[26]提出了一种基于粒子滤波(Particle Filter,PF)的SLAM算法，(Rao-Blackwellised Particle Filter,RBPF)算法，该算法通过把状态估计中后验概率的分布分成位姿估计和建图两部分，把SLAM问题分成定位和建图两个模块，极大的减少了SLAM的计算量。在这之后Montemerlo等人[27]提出在定位模块使用PF和在建图模块使用KF的FastSLAM 2.0算法。Jureviius等人[28]在基于PF的基础上采用先定位后建图的思想，改进粒子分布，加入了选择性重采样机制，删除了回环检测，使机器人能够快速定位。

        与KF的原理不同依靠PF的SLAM算法，能够直接应用到非线性系统中，并且不会出现高斯噪声，使系统具有良好的通用性，但是由于每一枚粒子都携带一幅地图，因此构建结构化地图时计算量非常大难以构建全局地图[29]。

        而基于优化的SLAM算法在构建结构化的地形时有着良好的性能。Gutmann等人[30]提出了包括闭环检测、位姿修正和帧与帧间校准的基于图优化的SLAM框架。根据优化思路的不同又可以将其分为基于最小二乘法或者基于分支上界法思想的基于图优化的SLAM算法[31]。最小二乘法是求解基于图优化的SLAM的经典方法。Kaess等人[32]使用基于最小二乘法的增量结构来优化姿态，能够在运动的同时进行姿态修正，并提出了ISAM 2.0算法。而Dellaert等人提出的SAM算法[33]和Liu等人改进的2DSLAM算法[34]，是根据基于最小二乘法的批量结构，能够快速定位，并且在结构化的环境中能够良好建图。直到2016年谷歌公司开发的Cartographer算法[35]，采用分支上界法，在有限的计算资源中实现了图优化所需的回环检测。

 

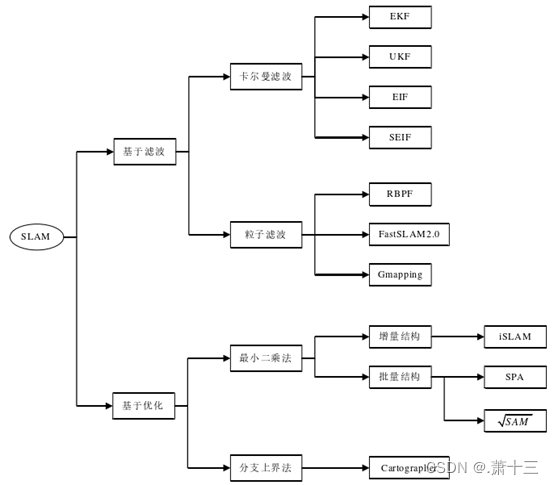
图1  SLAM技术分类

        综上所述，在室内环境这种结构化的环境中基于滤波的SLAM算法计算速度快，但是随着地图的增大计算量也会增加，无法构建全局一致的地图[36]。基于优化的SLAM对结构化的室内环境采集效率高，框架完整，响应速度快。适合无人机的室内建图和定位。

2. 无人机定位研究现状

        上一小节中对国内外SLAM算法的研究现状进行了阐述。无人机的全局定位可以被描述成在Bayes理论下，提取无人机机载传感器感知到的环境信息，对自身在环境中求解位姿的过程[37]。 Rone[38]使用卡尔曼滤波递归求解系统的状态方程，使其能够进行全局定位，但是因为使用KF无法使其应用在非线性的系统中，这使得这种方法只能在理想环境中使用。Roumeliotis等人[39]为了能在非线性系统中工作提出了基于EKF的定位算法，但是由于EFK所需要大量计算量，导致计算困难，并且存在计算精度低等问题。Kelly等人使用UKF进行全局定位，不再需要求解雅可比矩阵和高阶偏导数，同时也可以应用在非线性系统中。

        马尔可夫(Markov)定位方法是由Martinelli 等人[40]提出的属于Bayes理论的一个变种，并由Milford等人将其实现在栅格地图中，但是马尔可夫定位方法随着场景结构的复杂度的增加，计算量也显著增加，不适合在大型的非结构化空间中定位。在这之后基于拓扑图的马尔可夫定位算法简化了概率分布的表示，减少了计算量，但定位精度不够，依然难以在非结构化环境中应用。

        蒙特卡洛定位(MCL)算法是经典的全局定位算法[41]。该方法利用一组离散分布的加权随机粒子来估计机器人位姿的概率分布，可以同时考虑定位过程的时间和空间复杂度。Hennes等人[42]针对MCL中粒子数过大等问题，提出一种基于采样数的自适应MCL算法。2020年李振刚[43]针对粒子收敛速度慢、定位不精确等问题设计融合多种传感器的自适应MCL算法，提高了定位精度。

        此外还有基于深度强化学习的无人机自主定位方法[44]，针对一般算法的计算资源的浪费、实时性差等缺点，提出了适用于无人机的强化学习框架，比起一般的定位算法，定位精度、实时性和鲁棒性都有了显著提升，但是基于深度强化学习方法的无人机自主定位，没有办法在陌生的环境中定位，局限性和定位效率上交MCL算法差。

        综上所述，MCL定位算法是一种有效且应用广泛的机器人全局定位算法，但是MCL的时间复杂度与粒子数成线性关系，并且只能结合一个传感器。为此有必要使用EKF将多个传感器的测量数据融合起来，并且添加自适应机制，使其能够精准定位的同时也能减少定位的时间。

3 路径规划的研究现状

        自主导航的能力是无人机能否在室内环境下安全条件之一，自主导航的核心问题是如何解决无人机安全、稳定并且快速的到达指定位置，路径规划按照功能的不同主要可以分为局部和全局路径规划[45]，其中局部路径规划可以应对未知环境下的动态路径规划，全局路径规可以给出两点之间的最优（短）路径。

        如图1-2所示，根据路径规划的发展趋势可以分为基于图搜索的Dijkstra(Dij)算法、A*算法、D*算法、Theta*算法和Phi*算法，基于采样的随机路标图(PRM)和随机搜索树(RRT)算法，局部规划算法主流的有人工势能法(APF)和动态窗口法(DWA)。

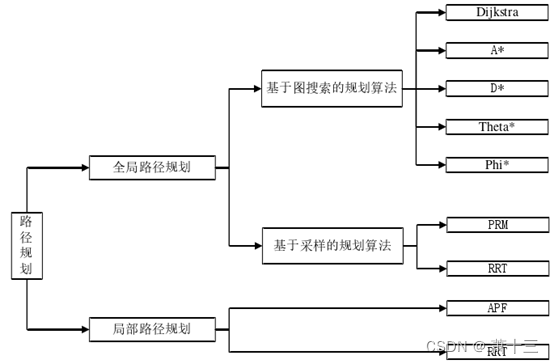
图2 路径规划分类

        在全局规划算法中首次使用启发函数的A*算法和能够解决APF算法的局部最优解的PRM应用的最为广泛，在国内外研究中针对两种算法搜索效率提出了一些改进。

        西安理工大学的吴欣[46]将距离信息以指数函数的形式最为启发函数，采用梯度下降法平滑路径，降低了节点的重复搜索概率，但是没有考虑转折点速度和转折点数量。

        迟旭[47]等人将A*和DWA算法融合，通过对A*算法得到的局部目标点进行迭代更新使水面无人艇利用DWA得到最佳搜索路径，使机器人能够进行动态避障，但是搜索速度有待提高，面对复杂环境和需要快速变化航向角时产生转折点数量过多。

        西南科技大学的曾润[48]把跳转点思想引入A*，加快了搜索路径的速度，通过修改启发函数减少转折点，并基于无人机的飞行特征对规划路径进行优化，得到改进后的A*算法，但在室外环境中由于障碍物不多，基于跳转点思想的A*算法，会盲目地寻找跳转点降低搜索效率，导致路径规划效率慢。

        Stentz提出适用于动态环境的改进型A*算法即D*算法。王琼[49]以Theta*算法为研究对象，提出双向优化的Theta*算法，解决了路径无效转折等问题，并从环境的复杂度角度对算法进行改进，最终提出融合环境信息的双向Theta*算法。

        基于采样的规划算法主要分为两类，一类是随机地图法(PRM)另一类是快速随机搜索树(RRT)。PRM算法是由Overmars等人[50]在1992年提出的。首先环境中的随机采集散点，然后将采样点进行连通，构建无向连通图，然后在无向连通图中进行路径搜索。PRM的难度主要取决于生成的拓扑空间的复杂性。近年来，许多研究者将PRM算法应用于无人机自主飞行的路径规划上。ANKIT等人[51]将PRM和APF相结合使机器人能够在平面空间中动态避障，通过在地图中设定高低势能区域设计出一种减少样本集分散的HPRM算法。RRT算法[52]在规划空间中随机向任意方向拓展节点，并在被覆盖的空间寻找目标点，然后将起点到目标点间的最短的连线距离连接成路径，但是如果是结构化的室内环境就会陷入像房间角落这样的狭小空间中，导致RRT算法无法得到一个最短路径。林娜等人[53]基于动态快速探索随机树(RRT)，提出了基于动态步长和自适应权重数值的RRT算法。

        局部规划算法中APF和DWA是常用的路径规划算法。人工势能法是由khatib等人[54]最早在1986年所提出的，APF算法假设载体始终处于一个虚拟力场中，周围所有物体都对其产生斥力，只有目标点提供引力，通过计算这一时刻的合力并按照合力方向进行局部路径规划。DU等人[55]根据动态人工势能法(D-APF)设计无人机实时无碰撞的避障路径。曹凯等人[56]为了提高移动机器人在动态环境下路径规划的效率和有效性，提出了一种融合了RRT和APF的方法，在APF算法陷入局部最小值时，使用RRT算法进行重新规划，解决了APF算法会陷入局部最小值的问题。Seder等人[57]考虑了载体的速度变化，并根据速度变化量把采样范围限制在一个动态窗口中，以此提出了DWA算法。 综上所述，要想让无人机在室内进行自主飞行任务，全局规划和局部规划缺一不可，全局路径规划可以保证无人机在已知的全局范围内进行最优路径规划；局部路径规划能保证无人机在全局地图时出现动态障碍或者未知障碍时的安全。

参考文献

[21] Ristic B, Palmer L. Autonomous Exploration and Mapping with RFS Occupancy-Grid SLAM [J]. Entropy, 2018, 20(6): 8.

[22] Radmanesh M , Kumar M , Nemati A , et al. Dynamic optimal UAV trajectory planning in the National Airspace System via mixed integer linear programming [J]. Proceedings of the Institution of Mechanical Engineers Part G Journal of Aerospace Engineering, 2016, 13(g9): 140-50.

[23] 孙海波, 童紫原, 唐守锋, 等.基于卡尔曼滤波与粒子滤波的SLAM研究综述[J]. 软件导刊, 2018, 17(12): 1-3+7.

[24] S Pérez-Carabaza, Sch Erer  J, B  Rinn er , et al. UAV trajectory optimization for Minimum Time Search with communication constraints and collision avoidance [J]. Engineering Applications of Artificial Intelligence, 2019,  85(October 2019): 357-371.

[25] 施俊屹, 查富生, 孙立宁, 等. 移动机器人视觉惯性SLAM研究进展[J]. 机器人, 2020, 42(06): 734-748.

[26] 黄辉, 邹安安, 胡鹏, 等. 基于Rao-Blackwellized粒子滤波器移动机器人SLAM研究[J]. 测控技术, 2021, 40(06): 46-50.

[27] Liu J, Wang X, Bai B, et al. Age-Optimal Trajectory Planning for UAV-Assisted Data Collection [J]. 2018: 553-558.

[28] Jureviius R, Marcinkeviius V, Eibokas J. Robust GNSS-denied Localization for UAV Using Particle Filter and Visual Odometry[J]. Machine Vision and Applications, 2019, 30(2): 1181-1190.

[29]  D'Amato E, Nardi V A, Notaro I, et al. A Particle Filtering Approach for Fault Detection and Isolation of UAV IMU Sensors: Design, Implementation and Sensitivity Analysis[J]. Sensors, 2021, 21(9): 3066-3068.

[30] Vujasinovi S , Becker S , Breuer T , et al. Integration of the 3D Environment for On-Board UAV Visual Object Tracking[J]. Applied Sciences, 2020, 21(2): 7622-7628.

[31] Liu T, Chen Y, Jin Z, et al. Spare Pose Graph Decomposition and Optimization for SLAM[J]. MATEC Web of Conferences, 2019, 256: 503-507.

[32] Chamseddine A, Theilliol D, Zhang Y M, et al. Active fault-tolerant control system design with trajectory re-planning against actuator faults and saturation: Application to a quadrotor unmanned aerial vehicle [J]. International Journal of Adaptive Control & Signal Processing, 2015, 29(1): 1-23.

[33] Xia Q, Liu S, Guo M, et al. Multi-UAV trajectory planning using gradient-based sequence minimal optimization [J]. Robotics and Autonomous Systems, 2021,  137(4): 103728-103735.

[34] Li, Fuxing; Liu, Shenglan, et al. Real-Time 2-D Lidar Odometry Based on ICP[J]. Sensors, 2021, 21(21): 7162-7171.

[35] Zhi Cui, Zhaohua Liu, Yong Li, et al. Optimal Parameter Analysis of Two 2D Lidar SLAM[J]. World Scientific Research Journal, 2020, 6(1): 56-62

[36] 徐梦溪, 陆云扬, 谈晓珊, 等. 固态激光雷达传感器技术及无人机载测深应用[J]. 电子测量技术, 2021, 44(15): 89-96.

[37] 施俊屹,查富生,孙立宁,等. 移动机器人视觉惯性SLAM研究进展[J]. 机器人, 2020, 42(06): 734-748.

[38] Rone W S, Bentzvi P. Mapping, Localization and Motion Planning in Mobile Multi-Robotic Systems [J]. Robotica, 2013, 31(01): 1-23.

[39] 张千坤, 钟志刚, 陈任翔, 等. 基于抗差EKF的Wi-Fi/MEMS融合室内定位算法[J]. 邮电设计技术, 2021, 11(1): 35-41.

[40] 陈勇, 巫杰, 刘焕淋, 等. 基于隐马尔可夫模型的可见光与惯导融合室内定位系统[J]. 中国激光, 2020, 47(12): 238-245.

[41] Radmanesh M, Cohen K, Kumar M. Large-Scale UAV Trajectory Planning Using Fluid Dynamics Equations [J]. Multi-Rotor Platform-based UAV Systems, 2020: 63-86.

[42] Hennes D, Claes D, Meeussen W, et al. Multi-robot Collision Avoidance with Localization Uncertainty [J]. Adaptive Agents and Multi-agents Systems, 2012: 147-154.

[43] 李振刚. 基于ROS的室内智能轮椅系统研究[D]. 湖北: 武汉理工大学, 2019: 7-8.

[44] Zhao Jiang, Sun Jiaming, Wang Longhong, et al. End-to-End Deep Reinforcement Learning for Image-based UAV Autonomous Control[J]. Applied Sciences, 2021, 11(18): 8419.

[45] Tang Bijun; Hirota Kaoru; Wu, Xiangdong, et al. Path Planning Based on Improved Hybrid A* Algorithm[J]. Journal of Advanced Computational Intelligence and Intelligent Informatics, 2021, 25(1): 64-72.

[46] 吴欣. ROS下移动机器人激光雷达地图构建与路径规划研究[D]. 陕西: 西安理工大学,2021: 9-10.

[47] 迟旭, 李花, 费继友. 基于改进A~*算法与动态窗口法融合的机器人随机避障方法研究[J]. 仪器仪表学报, 2021, 42(03): 132-140.

[48] 曾润. 无GNSS支持的无人机定位与路径规划技术研究[D]. 四川: 西南科技大学, 2021: 3-4.

[49] 王琼, 于登云, 贾阳. 一种基于地形方向通行性的改进Theta*算法[J]. 空间科学学报, 2016, 36(03): 401-406.

[50] Park B; Chung W K. Efficient Environment Representation for Mobile Robot Path Planning Using CVT-PRM with Halton Sampling [J]. Electronics Letters, 2012, 48(22): 1-2.

[51] Ravankar A, Ravankar A, Emaru T, et al. HPPRM: Hybrid Potential Based Probabilistic Roadmap Algorithm for Improved Dynamic Path Planning of Mobile Robots[J]. IEEE Access, 2020, 8:221743-221766.

[52] 赵惠, 李庆党, 张明月. 基于改进RRT算法的机械臂路径规划方法[J].电子测量技术, 2021, 44(16): 45-49.

[53] 林娜,张亚伦.自适应RRT无人机航路规划算法研究与仿真[J].计算机仿真,2015,32(01):73-77.

[54] 徐小强,宋子奇,冒燕,郭利荣.基于APF-RRT*融合算法的无人机全局路径规划研究[J].武汉理工大学学报,2021,43(09):72-78.

[55]  Du Y, Zhang X, Nie Z. A Real-Time Collision Avoidance Strategy in Dynamic Airspace Based on Dynamic Artificial Potential Field Algorithm[J]. IEEE Access, 2019, 99(01):169469-169479.

[56] 曹凯, 陈阳泉, 高嵩, 等. 涡流人工势场引导下的RRT~*移动机器人路径规划[J].计算机科学与探索, 2021, 15(04): 723-732.

[57] 陈方正, 郝绍杰. 动态威胁环境下单无人机测向定位航迹优化算法[J].国防科技大学学报, 2021, 43(05): 137-143.