- 1iFlytekSpark_iflytekspark-13b
- 2javascript高级程序设计 -- 读书笔记(二) _classa red classb blue文字是什么颜色
- 3ChatGPT 深度解析:技术驱动的智能对话
- 4亚马逊云科技AWS免费大热AI应用开发证书和AI大语言模型开发代码案例
- 5python PyQt5中文教程☞【第五节】PyQt5事件(Event)和信号(信号槽 Signals & slots)_【第五节】pyqt5事件和信号-pyqt5中文教程
- 6校园物业报修小程序开发笔记一_校园维修小程序功能性需求
- 7Spring Boot常见面试题_springboot常见面试
- 8Gradio从入门到精通(8)---基础组件介绍2
- 9绝对的好文,有点长,耐心点,说不定你的人生因此改变
- 10iOS 开发者的 Flutter 入门课
LSH算法:高效相似性搜索的原理与Python实现II_lsh python
赞
踩
局部敏感哈希(LSH)是一种高效的近似相似性搜索技术,广泛应用于需要处理大规模数据集的场景。在当今数据驱动的世界中,高效的相似性搜索算法对于维持业务运营至关重要,它们是许多顶尖公司技术堆栈的核心。
相似性搜索面临的主要挑战在于处理庞大的数据规模。许多企业每天都要处理从百万到数十亿不等的数据点。例如,面对一亿个数据点,逐个进行比较显然是不切实际的。
更进一步,企业的需求远不止单次搜索。以谷歌为例,它每分钟处理的搜索请求超过380万次。这种高频率的搜索需求,再加上数据点的规模,构成了一个巨大的技术挑战。
此外,还没有涉及到数据的维度问题或相似性函数的复杂性。在这些因素的共同作用下,对于大型数据集进行全面的搜索变得不可行。
那么,如何在如此难以想象的大规模数据集上进行有效搜索呢?答案就是近似搜索。通过近似搜索,不必对每一对数据点进行详尽的比较。相反,采用LSH技术,它通过近似方法筛选出潜在的匹配项,从而大幅减少了需要进行详尽比较的数据点数量。
通过这种方式,LSH不仅提高了搜索效率,还保持了搜索结果的准确性,使其成为大规模数据集相似性搜索的理想解决方案。
局部敏感哈希(LSH)
局部敏感哈希(LSH)是一种广泛使用的近似最近邻搜索(ANNS)方法。它依赖于一种特殊的哈希函数,这种函数设计用来将相似的项目映射到同一个哈希桶中。面对大规模数据集,LSH通过哈希函数将项目分配到不同的桶,从而简化搜索过程。
LSH算法的一个关键特点是它与常规哈希函数不同。传统哈希函数致力于最小化哈希冲突,而LSH算法则有意增加哈希冲突的概率,目的是将相似的项目聚集在一起。
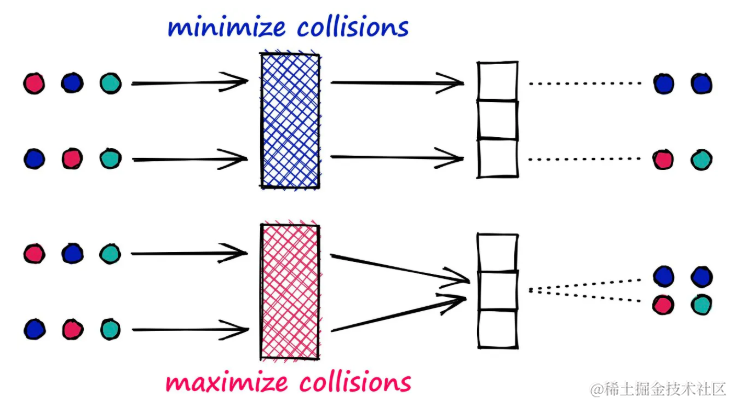
哈希函数对比:上图展示了两种哈希函数的效果。顶部(蓝色)的哈希函数致力于最小化哈希冲突,而底部(品红色)的哈希函数则是LSH使用的,它旨在最大化相似项之间的哈希冲突。
在LSH中,相似的向量倾向于产生相同的哈希值,并因此被分到同一个桶里。相对地,不相似的向量则希望不会被分到同一个桶中。
使用LSH进行搜索
LSH搜索过程包括以下三个步骤:
- 索引向量:首先,将所有向量通过LSH哈希函数处理,并将它们索引到对应的哈希桶中。
- 哈希查询向量:当引入一个查询向量时,使用相同的LSH哈希函数对其进行处理。
- 桶比较:然后,通过比较汉明距离来识别查询向量与哪些哈希桶中的向量最近。
这些步骤构成了LSH方法论的基础,将在后续的文章中对这些概念进行更深入的探讨和详细说明。
近似效果
在深入研究LSH技术之前,重要的是要认识到,通过将向量映射到低分辨率的哈希向量中,实际上是在进行一种近似处理。这种方法意味着搜索过程可能不会详尽无遗地比较每个向量,因此预期搜索的精确度会有所降低。
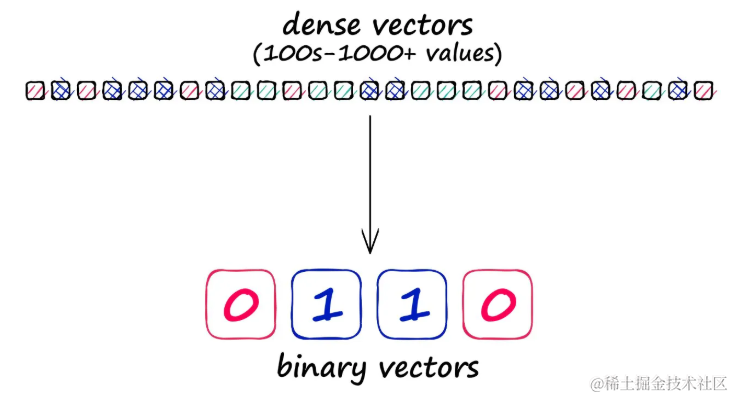
将可能非常大的密集向量压缩成高度压缩的二进制向量,以实现更快的搜索速度。虽然这种压缩牺牲了一定的搜索质量,但它显著提高了搜索效率。
方法选择
LSH有多种实现方式,每种方法使用不同的哈希构建技术和距离或相似度度量。在这里不深入细节,因为不同的版本适用于不同的应用场景。
最受欢迎的两种LSH实现方法是:
- 文档分片、MinHashing和带状LSH:这是一种较为传统的LSH方法,适用于特定类型的数据集和查询。
- 随机超平面与点积和汉明距离:这种方法使用随机超平面来构建哈希函数,并通过点积和汉明距离来衡量向量间的相似性。
本文将专注于介绍随机超平面方法,它不仅更常用,而且在多个流行库中得到了实现,例如Faiss。这种方法因其高效性和易于实现的特点,在工业界和学术界都受到了广泛的关注。
随机超平面(Random Hyperplanes)
随机超平面方法,尽管听起来简单,实际上是一种高效的技术,用于在高维空间中进行近似最近邻搜索。这种方法可能难以理解,但通过以下示例,将深入探讨其工作原理。
这里使用Sift1M数据集进行示例。假设我们有一个查询向量xq,目标是从数组xb中识别出前k个最近邻。
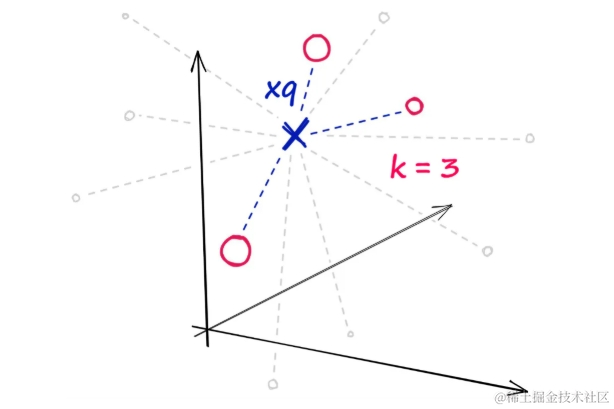
返回查询向量
xq的三个最近邻
创建超平面
在随机超平面方法中,通过构建超平面来分割数据点。每个超平面由一个法向量定义,数据点根据与法向量的点积结果被分配为0或1。
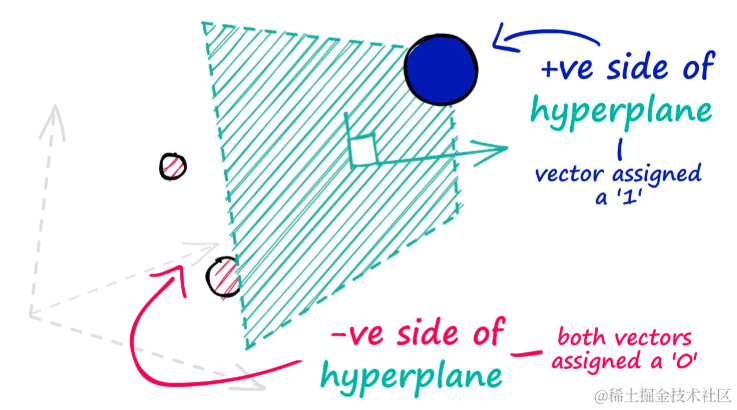
位于超平面正侧的数据点分配值1,为负侧的数据点分配值0
确定数据点位于超平面哪一侧的关键在于超平面的法向量。点积的结果告诉数据点位于超平面的哪一侧。如果两个向量方向相同,点积结果为正。如果它们方向不同,结果为负。
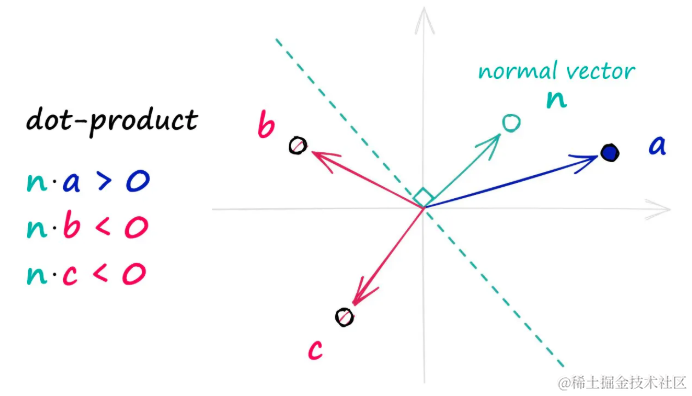
当超平面法向量与另一个向量产生 +ve 点积时,可以将该向量视为位于超平面前面。对于产生 -ve 点积的向量来说,情况正好相反
在两个向量完全垂直(位于超平面边缘)的极少数情况下,点积为0——将这种情况归入负方向向量。
单个二进制值并不能告诉太多关于向量相似性的信息,但当添加更多超平面时,编码的信息量会迅速增加。
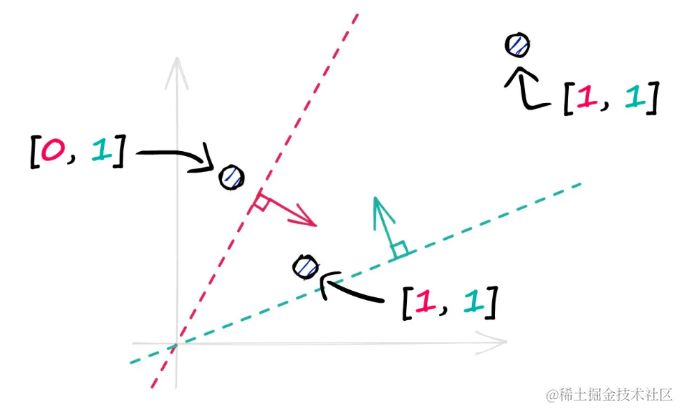
添加更多超平面来增加二进制向量中存储的位置信息量。
通过使用这些超平面将向量投影到低维空间中,产生新的哈希向量。
在上图中,使用了两个超平面,实际上可能需要更多——这个特性通过nbits参数定义。如果使用四个超平面,通过将nbits设置为4。
在Python中创建超平面的法向量。
nbits = 4 # 超平面的数量
d = 2 # 向量的维度
import numpy as np
# 创建一组随机法向量
plane_norms = np.random.rand(nbits, d) - .5
plane_norms
- 1
- 2
- 3
- 4
- 5
- 6
- 7
array([[-0.26623211, 0.34055181],
[ 0.3388499 , -0.33368453],
[ 0.34768572, -0.37184437],
[-0.11170635, -0.0242341 ]])
- 1
- 2
- 3
- 4
通过 np.random.rand 创建了一组 0 → 1 范围内的随机值。然后添加-.5使数组值以原点 (0, 0) 为中心。可视化这些向量:
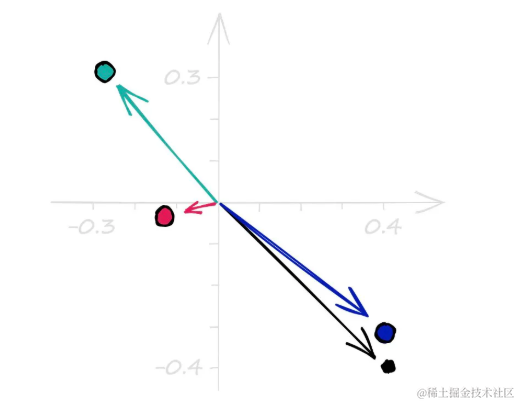
定义超平面位置的法向量,均以原点 (0, 0) 为中心
哈希向量
给定几个向量,可以使用这些法向量来计算它们的哈希值。
a = np.asarray([1, 2]) b = np.asarray([2, 1]) c = np.asarray([3, 1]) # 计算点积 a_dot = np.dot(a, plane_norms.T) b_dot = np.dot(b, plane_norms.T) c_dot = np.dot(c, plane_norms.T) a_dot # array([ 0.41487151, -0.32851916, -0.39600301, -0.16017455]) a_dot = a_dot > 0 b_dot = b_dot > 0 c_dot = c_dot > 0 a_dot # array([ True, False, False, False]) # 将点积结果转换为二进制值 a_dot = a_dot.astype(int) b_dot = b_dot.astype(int) c_dot = c_dot.astype(int) a_dot # array([1, 0, 0, 0]) b_dot # array([0, 1, 1, 0]) c_dot # array([0, 1, 1, 0])
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
再次可视化,得到了三个向量 a、b 和 c,以及四个超平面(垂直于它们各自的法向量)。分别取 +ve 和 -ve 点积值得出:
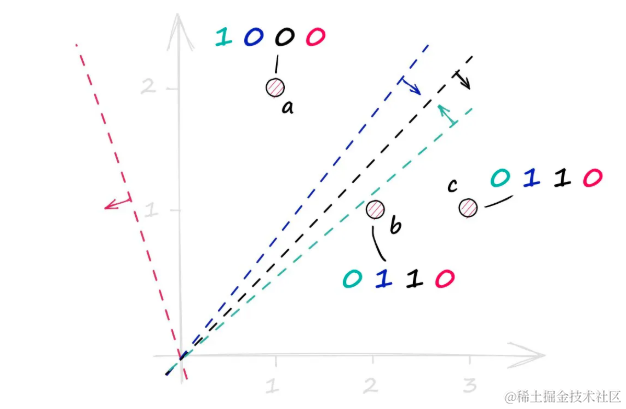
0表示矢量位于平面后面(-ve 点积),1表示矢量位于平面前面(+ve 点积),组合起来创建二进制向量
LSH使用哈希向量来创建桶,每个桶包含具有相同哈希值的向量。
vectors = [a_dot, b_dot, c_dot]
buckets = {}
i = 0
for i in range(len(vectors)):
hash_str = ''.join(vectors[i].astype(str))
if hash_str not in buckets.keys():
buckets[hash_str] = []
buckets[hash_str].append(i)
print(buckets)
# {'1000': [0], '0110': [1, 2]}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
现在搜索过程中,使用查询向量0111的哈希值来快速定位到相关的桶,然后通过比较汉明距离来找到最近的匹配。
使用这个向量,与LSH索引中的每个桶进行比较——在这个例子中只有两个值——1000和0110。使用汉明距离找到最近的匹配,这实际上是0110。
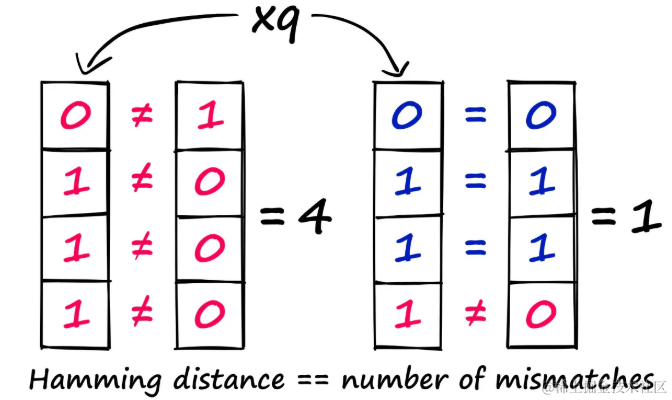
汉明距离,第一个两个向量之间有四个不匹配,汉明距离为4,接下来的两个只包含一个不匹配,汉明距离为1
使用LSH进行近似搜索意味着可能会牺牲一些搜索质量,但这是换取速度的代价。通过分组到桶中,显著减少了搜索所需的计算量。
平衡质量与速度
在相似性搜索中,一个关键的挑战是在搜索质量和速度之间找到合适的平衡点。
质量与速度的平衡
以我们的小规模示例为起点,注意到随机投影可能导致一些向量难以区分,例如,三个向量中的两个被映射到了相同的哈希值。现在,设想将这种情况放大到一个包含一百万个向量的大型数据集。
当引入查询向量xq并计算其哈希值(例如0111)时,发现它与两个桶(1000和0110)的汉明距离非常短。这种方法的速度非常快,因为它只需要两次距离计算就完成了搜索,但准确性却大大降低,因为可能返回了大约70万个哈希值为0110的样本。
桶的数量
在现实中,如果使用nbits值为4,将得到16个可能的桶:
nbits = 4
# 计算nbits值的二进制组合数
1 << nbits # 16
# 打印给定nbits值的所有可能桶
for i in range(1 << nbits):
# 获取整数的二进制表示,并格式化为nbits位
b = bin(i)[2:]
b = '0' * (nbits - len(b)) + b
print(b, end=' | ')
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
- 1
即使有16个桶,一百万个向量被分成的桶数量仍然很少,导致每个桶内的样本非常不精确。
提高分辨率
为了提高搜索质量,可以通过增加超平面的数量来增加分辨率。更多的超平面意味着更高的分辨率二进制向量,从而产生更精确的向量表示。
通过nbits值来控制这种分辨率。一个更高的nbits值通过增加哈希向量的分辨率来提高搜索质量,但同时也可能增加搜索的计算成本。
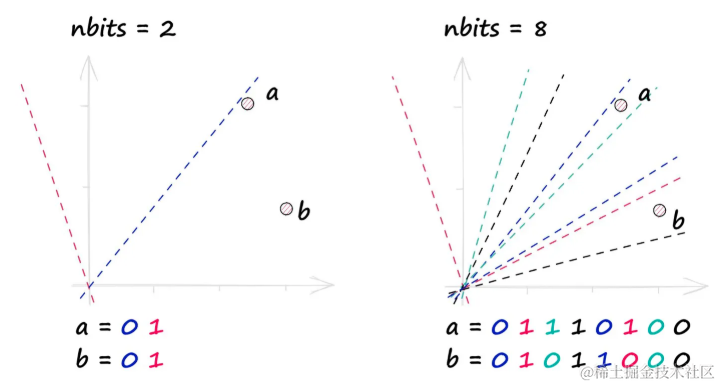
增加
nbits参数会增加用于构建二进制向量表示的超平面的数量
for nbits in [2, 4, 8, 16]:
print(f"nbits: {nbits}, buckets: {1 << nbits}")
- 1
- 2
nbits: 2, buckets: 4
nbits: 4, buckets: 16
nbits: 8, buckets: 256
nbits: 16, buckets: 65536
- 1
- 2
- 3
- 4
通过调整nbits值,可以在搜索质量和速度之间进行权衡。在实际应用中,选择合适的nbits值是实现高效相似性搜索的关键。
Faiss中的LSH
回顾Faiss
Faiss(Facebook AI Similarity Search)是一个开源框架,专门用于高效实现相似性搜索。它提供了多种索引类型,包括IndexLSH,这是之前讨论过的局部敏感哈希(LSH)的高效实现。
初始化LSH索引
在Faiss中初始化LSH索引并添加数据集的示例代码如下:
import faiss
d = wb.shape[1] # 向量维度
nbits = 4 # 控制哈希向量的分辨率
# 初始化LSH索引
index = faiss.IndexLSH(d, nbits)
# 添加数据集
index.add(wb)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
执行搜索
一旦索引准备好,可以使用index.search(xq, k)方法进行搜索,其中xq是查询向量,k是希望返回的最近匹配数量。
xq0 = xq[0].reshape(1, d) # 查询向量
# 搜索k个最近邻
D, I = index.search(xq0, k=10)
# 返回最近邻的索引和距离
print("Indexes:", I) # 索引位置
print("Distances:", D) # 距离
- 1
- 2
- 3
- 4
- 5
- 6
测量性能
使用返回的索引,可以从数据集中检索原始向量,并计算它们与查询向量之间的余弦相似度。
# 检索原始向量
retrieved_vectors = wb[I[0]]
# 计算余弦相似度
cosine_sim = cosine_similarity(retrieved_vectors, xq0)
print("Cosine Similarity:", cosine_sim)
- 1
- 2
- 3
- 4
- 5
array([[0.7344476 ],
[0.6316513 ],
[0.6995599 ],
[0.20448919],
[0.3054034 ],
[0.25432232],
[0.30497947],
[0.341374 ],
[0.6914262 ],
[0.26704744]], dtype=float32)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
从那些原始向量中,可以看到LSH索引是否返回了相关结果。通过测量查询向量xq0与前k个匹配之间的余弦相似性来进行这一操作。这个索引中有向量应该返回大约0.8的相似度分数,但返回的向量相似度分数仅为0.2,反映出性能低下。
诊断性能问题
如果返回的相似度分数较低,需要诊断性能问题。nbits值决定了索引中潜在桶的数量。如果nbits设置得太低,可能导致大量向量被分配到少数几个桶中,从而降低搜索质量。
如果尝试将1M个向量塞进只有16个哈希桶中,每个桶很可能包含10-100K+个向量。
所以,当哈希搜索查询时,它完美地匹配了这16个桶中的一个——但是索引无法区分被塞进那个单个桶中的大量向量——它们都有相同的哈希向量。可以通过检查距离D来确认这一点:
print(D)
# array([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0.]], dtype=float32)
- 1
- 2
返回每个项目的完美距离分数为零,汉明距离只有在完美匹配时才能为零——这意味着所有的这些哈希向量必须是相同的。
如果所有的这些向量都返回完美匹配,它们必须都有相同的哈希值。因此,上述生成的索引无法区分它们——就LSH索引而言,它们都共享相同的位置。
如果增加k直到返回一个非零的距离值,应该能够推断出有多少个向量被分桶了这个相同的哈希码。
k = 100
xq0 = xq[0].reshape(1, d)
while True:
D, I = index.search(xq0, k=k)
if D.any() != 0:
print(k)
break
k += 100
print(D)
print(D[:, 172039:172041])
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
172100
array([[0., 0., 0., ..., 1., 1., 1.]], dtype=float32)
array([[0., 1.]], dtype=float32)
- 1
- 2
- 3
一个包含172,039个向量的单个桶,这意味着是在从这172K个向量中随机选择前k个值。显然,需要减少桶的大小。
对于1M个样本,哪个nbits值有足够的桶以实现向量的更稀疏分布,通过计算平均值进行估计:
for nbits in [2, 4, 8, 16, 24, 32]:
buckets = 1 << nbits
print(f"nbits == {nbits}")
print(f"{wb.shape[0]} / {buckets} = {wb.shape[0]/buckets}")
- 1
- 2
- 3
- 4
nbits == 2
1000000 / 4 = 250000.0
nbits == 4
1000000 / 16 = 62500.0
nbits == 8
1000000 / 256 = 3906.25
nbits == 16
1000000 / 65536 = 15.2587890625
nbits == 24
1000000 / 16777216 = 0.059604644775390625
nbits == 32
1000000 / 4294967296 = 0.00023283064365386963
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
使用nbits值为16时,仍然在每个桶中得到大约15.25个向量——这看起来比实际情况要好。必须考虑到,有些桶会比其他桶大得多,因为不同的区域会包含更多的向量。
实际上,nbits值为24和32可能是实现真正有效桶大小的转折点。
xq0 = xq[0].reshape(1, d)
k = 100
for nbits in [2, 4, 8, 16, 24, 32]:
index = faiss.IndexLSH(d, nbits)
index.add(wb)
D, I = index.search(xq0, k=k)
cos = cosine_similarity(wb[I[0]], xq0)
print(np.mean(cos))
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
0.5424448
0.560827
0.6372647
0.6676912
0.7162514
0.7048228
- 1
- 2
- 3
- 4
- 5
- 6
看起来估计是正确的——前100个向量的整体相似度在每个nbits值增加之前突然上升,在
n
b
i
t
s
=
=
24
nbits == 24
nbits==24点之前稳定下来。
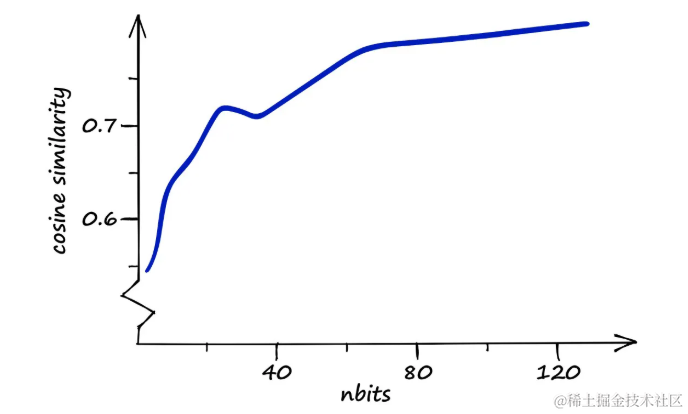
随着nbits值增加向量分辨率,结果将变得更加精确——可以看到更大的nbits值导致结果中余弦相似度更高。
提取二进制向量
Faiss允许提取向量的二进制表示,这有助于直接分析桶中的向量分布。
# 提取二进制代码
arr = faiss.vector_to_array(index.codes)
arr # array([ 5, 12, 5, ..., 15, 13, 12], dtype=uint8)
arr.shape # (1000000,)
# 将整数转换为二进制向量格式
(((arr[:, None] & (1 << np.arange(nbits)))) > 0).astype(int)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
array([[1, 0, 1, 0],
[0, 0, 1, 1],
[1, 0, 1, 0],
...,
[1, 1, 1, 1],
[1, 0, 1, 1],
[0, 0, 1, 1]])
- 1
- 2
- 3
- 4
- 5
- 6
- 7
通过这个,可以可视化这些16个桶中向量的分布——显示使用最多的桶和一些空的桶。
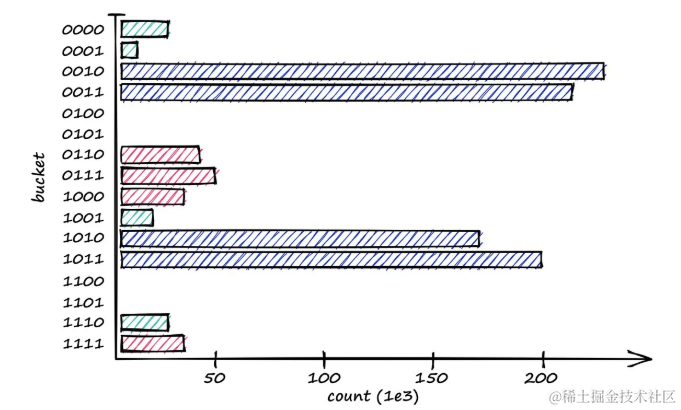
当nbits == 4时,不同桶中向量的分布
通过调整nbits值,可以在搜索质量和速度之间找到平衡。在Faiss中使用LSH时,理解不同参数如何影响性能对于优化搜索结果至关重要。
使用LSH
局部敏感哈希(LSH)提供了一种快速的索引机制,尽管它可能不如平面(Flat)索引准确。在Sift1M数据集上,通过逐渐增加数据集的大小,发现在nbits值设定为768时,可以实现最佳的召回率——尽管这需要牺牲一些搜索时间来获得更高的召回率。
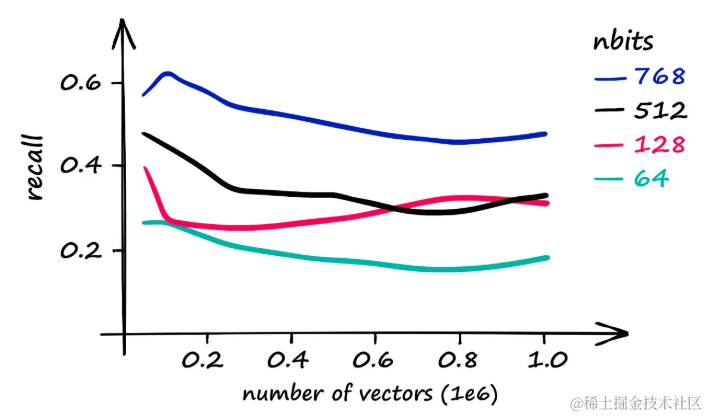
召回率与索引向量数量的关系:召回率是衡量搜索结果与使用IndexFlatL2进行详尽搜索的匹配程度的指标。
值得注意的是,即使使用nbits值为768,LSH的搜索速度也只是略快于平面Flat索引。
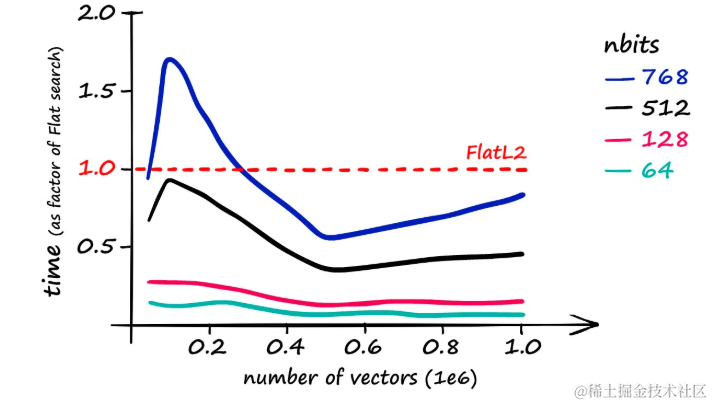
搜索时间的比较:展示了不同索引大小和
nbits值下,IndexFlatL2的搜索时间相对于其自身在不同条件下的变化。
在实际应用中,一个更现实的召回率目标是接近40%,同时保持合理的速度提升。数据集的大小和维度对LSH的性能有显著影响。随着维度的增加,为了保持准确性,可能需要使用更高的nbits值,但这仍有可能实现更快的搜索速度。关键在于为每个用例和数据集找到正确的平衡点。向量相似性搜索是一个多样化的领域,Flat索引和LSH只是众多选择中的两种。选择正确的索引策略需要结合实验和专业知识。
在相似性搜索中,始终需要在不同的索引选项和参数设置之间寻找最佳解决方案,这是一种平衡的行为。
总结
选择正确的相似性搜索算法取决于多种因素,包括数据集的大小和维度、搜索性能的要求,以及准确性的容忍度。LSH是众多工具中的一个,它在某些情况下表现出色,但也可能需要与其他技术相结合以达到最佳效果。除了LSH,还有许多其他算法适合于高效的相似性搜索,例如:
- HNSW(Hierarchical Navigable Small World):提供在大规模数据集上进行近似最近邻搜索的能力。
- IVF(Inverted File Index):通过聚类和索引减少搜索范围,提高了搜索速度。
- PQ(Product Quantization):一种量化技术,通过将向量空间划分为较小的子空间来加速搜索。
鼓励读者根据本文提供的信息,进行实验和探索,以找到最适合自己特定需求的搜索算法。



