devbox
知新_RL
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

transformer位置编码以及代码解释_transformer位置编码代码

作者：知新_RL | 2024-04-06 10:42:01

赞

踩

transformer位置编码代码

Transformer 是combination-invariant的。也就是说，混洗输入嵌入不会改变transformer的输出。然而，嵌入的位置也包含重要信息。为了使各自的模型意识到这一点，提出了许多不同的嵌入位置表示（Vaswani 等人，2017）。

Absolute Position Embedding

ViT

位置嵌入被加入到补丁嵌入中以保留位置信息。使用标准的可学习 1D 位置嵌入，因为没有观察到使用更先进的 2D 感知位置嵌入带来的显着性能提升。生成的嵌入向量序列用作编码器的输入。

  1. self.cls_token = nn.Parameter(torch.zeros(1, 1, embed_dim))
  2. self.pos_embed = nn.Parameter(torch.zeros(1, num_patches + self.num_tokens, embed_dim))
  3. self.pos_drop = nn.Dropout(p=drop_ratio)
  4. …
  5. nn.init.trunc_normal_(self.cls_token, std=0.02)
  6. nn.init.trunc_normal_(self.pos_embed, std=0.02)
  7. …
  8. x = self.patch_embed(x)  # [B, 196, 768]
  9. cls_token = self.cls_token.expand(x.shape[0], -1, -1)  #[B, 1, 768]
  10. x = torch.cat((cls_token, x), dim=1)  # [B, 197, 768]
  11. x = self.pos_drop(x + self.pos_embed)

代码知识：

# 创建两个tensor
a = torch.randn(2, 2, 1)
b = torch.randn(1, 2, 1)
# 直接相加不会会报错
c = a + b

PVT

vit是柱状结构，但是PVT不是柱状，所以在每一个stage均进行了重新编码。

  1. for i in range(num_stages):
  2.     pos_embed = nn.Parameter(torch.zeros(1, num_patches, embed_dims[i]))
  3.     pos_drop = nn.Dropout(p=drop_rate)
  4.  
  5.  
  6.     setattr(self, f"pos_embed{i + 1}", pos_embed)  
  7.

初始化：

  1.         for i in range(num_stages):
  2.             pos_embed = getattr(self, f"pos_embed{i + 1}")
  3.             trunc_normal_(pos_embed, std=.02)

重采样：

  1.     def _get_pos_embed(self, pos_embed, patch_embed, H, W):
  2.         if H * W == self.patch_embed.num_patches:
  3.             return pos_embed
  4.         else:
  5.             return F.interpolate(
  6.                 pos_embed.reshape(1, patch_embed.H, patch_embed.W, -1).permute(0, 3, 1, 2),
  7.                 size=(H, W), mode="bilinear").reshape(1, -1, H * W).permute(0, 2, 1)

前馈：

  1.         for i in range(self.num_stages):
  2.             patch_embed = getattr(self, f"patch_embed{i + 1}")
  3.             pos_embed = getattr(self, f"pos_embed{i + 1}")
  4.             pos_drop = getattr(self, f"pos_drop{i + 1}")
  5.             block = getattr(self, f"block{i + 1}")
  6.             x, (H, W) = patch_embed(x)
  7.  
  8.             if i == self.num_stages - 1:
  9.                 cls_tokens = self.cls_token.expand(B, -1, -1)
  10.                 x = torch.cat((cls_tokens, x), dim=1)
  11.                 pos_embed_ = self._get_pos_embed(pos_embed[:, 1:], patch_embed, H, W)
  12.                 pos_embed = torch.cat((pos_embed[:, 0:1], pos_embed_), dim=1)
  13.             else:
  14.                 pos_embed = self._get_pos_embed(pos_embed, patch_embed, H, W)
  15.  
  16.             x = pos_drop(x + pos_embed)
  17.             ...

Relative position bias

绝对位置编码是在计算注意力之前，直接将位置嵌入加到patch嵌入中。相对位置编码指的是在计算自注意力时，将相对位置偏差 B添加到嵌入的权重矩阵中。最近的许多工作（Liu 等人，2021b；Chen 等人，2021b）表明 RPB 的表现优于其他位置表示。

嵌入的长度为L（下图中L=6）,则权重矩阵表示每个嵌入互相之间的关系，所以大小为（L,L），因此B的大小也是（L,L）,表示的是每个嵌入之间的相对距离。

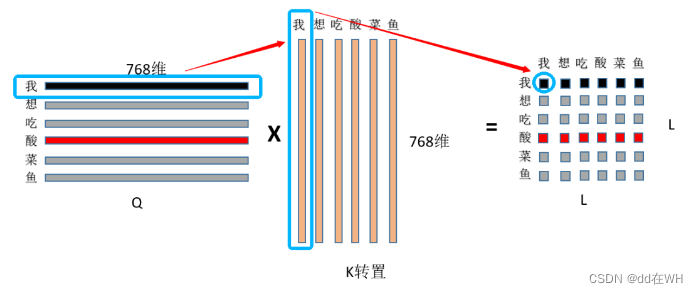
 Swin Transformer

例如：每个窗口包含M*M个patch，M=3，也就是嵌入长度为9，B的大小为（9,9）。对于M*M个patch，沿着行方向和列方向的相对位置取值在【-2,2】之间，因此先初始化一个（2M-1,2M-1）大小的偏置矩阵\widehat{B}。 偏置矩阵B的值则从\widehat{B}中获取。

初始化\widehat{B}

  1.     window_size = [3, 3]
  2.  
  3.     relative_position_bias_table = nn.Parameter(
  4.         torch.zeros((2 * window_size[0] - 1) * (2 * window_size[1] - 1)))
  5.     trunc_normal_(relative_position_bias_table, std=.02)
  6.     print(relative_position_bias_table)

[ 0.0170, -0.0079, -0.0149, -0.0078, -0.0052, -0.0192,  0.0162, -0.0523, 0.0186, -0.0113, -0.0179, -0.0243, -0.0049, -0.0174, -0.0311,  0.0066, 0.0098, -0.0068, -0.0029, -0.0073, -0.0181, -0.0250,  0.0035,  0.0284, -0.0055]  【注】以上只是其中一次初始化

接下来做的是从\widehat{B}中取值得到B，\widehat{B}中一共25个值，只要得到大小为（9,9）的下标矩阵，就可以从中取值，得到（9,9）的B。所以需要创建相对位置下标矩阵：

首先得到原始的相对位置关系：

  1.     coords_h = torch.arange(window_size[0])
  2.     coords_w = torch.arange(window_size[1])
  3.     coords = torch.stack(torch.meshgrid([coords_h, coords_w]))  # 2, Wh, Ww
  4.     coords_flatten = torch.flatten(coords, 1)  # 2, Wh*Ww
  5.     relative_coords = coords_flatten[:, :, None] - coords_flatten[:, None, :]  # 2, Wh*Ww, Wh*Ww
  6.     relative_coords = relative_coords.permute(1, 2, 0).contiguous()  # Wh*Ww, Wh*Ww, 2
  7.     print(relative_coords.shape, relative_coords)

torch.Size([9, 9, 2])   2个维度，分别表示行方向和列方向，比如第一行表示第一个patch嵌入与其他patch嵌入的相对位置关系

[ 0,  0]，[ 0, -1], [ 0, -2],     [-1,  0], [-1, -1], [-1, -2],    [-2,  0], [-2, -1],  [-2, -2]   #第一行数据

去除负数，每个数值均加2。

  1.     relative_coords[:, :, 0] += window_size[0] - 1  # shift to start from 0
  2.     relative_coords[:, :, 1] += window_size[1] - 1
  3.     print(relative_coords)

 [2, 2], [2, 1], [2, 0],   [1, 2],[1, 1], [1, 0],    [0, 2],[0, 1],[0, 0]    #第一行数据

二维相对位置改为一维相对位置：（如同读取二进制数据那样，计算出（i，j）在二进制数据的哪个位置）

  1.     relative_coords[:, :, 0] *= 2 * window_size[1] - 1
  2.     print(relative_coords.shape, relative_coords)

[10,  2], [10,  1],[10,  0],     [ 5,  2],[ 5,  1], [ 5,  0],   [ 0,  2],[ 0,  1],[ 0,  0]],   #第一行数据

  1.     relative_position_index = relative_coords.sum(-1)  # Wh*Ww, Wh*Ww
  2.     print(relative_position_index.shape, relative_position_index)

[12, 11, 10,  7,  6,  5,  2,  1,  0]   #第一行数据

整个相对位置下标矩阵为：

        [12, 11, 10,   7,  6,   5,   2,   1,   0],
        [13, 12, 11,   8,  7,   6,   3,   2,   1],
        [14, 13, 12,   9,  8,   7,   4,   3,   2],
        [17, 16, 15, 12, 11, 10,   7,  6,   5],
        [18, 17, 16, 13, 12, 11,   8,  7,   6],
        [19, 18, 17, 14, 13, 12,   9,   8,  7],
        [22, 21, 20, 17, 16, 15, 12, 11, 10],
        [23, 22, 21, 18, 17, 16, 13, 12, 11],
        [24, 23, 22, 19, 18, 17, 14, 13, 12]

B的值则是根据以上下标矩阵在\widehat{B}中取值。

  1.     relative_position_bias = relative_position_bias_table[relative_position_index.view(-1)].view(
  2.         window_size[0] * window_size[1], window_size[0] * window_size[1], -1)
  3.     relative_position_bias = relative_position_bias.permute(2, 0, 1).contiguous()
  4.     print(relative_position_bias)

[[[-0.0049, -0.0243, -0.0179, -0.0523,  0.0162, -0.0192, -0.0149, -0.0079,  0.0170],
  [-0.0174, -0.0049, -0.0243,  0.0186, -0.0523,  0.0162, -0.0078,  -0.0149, -0.0079],
  [-0.0311, -0.0174, -0.0049, -0.0113,  0.0186, -0.0523, -0.0052, -0.0078, -0.0149],
  [-0.0068,  0.0098,  0.0066, -0.0049, -0.0243, -0.0179, -0.0523,  0.0162, -0.0192],
  [-0.0029, -0.0068,  0.0098, -0.0174, -0.0049, -0.0243,  0.0186, -0.0523,  0.0162],
  [-0.0073, -0.0029, -0.0068, -0.0311, -0.0174, -0.0049, -0.0113,  0.0186, -0.0523],
  [ 0.0035, -0.0250, -0.0181, -0.0068,  0.0098,  0.0066, -0.0049, -0.0243, -0.0179],
  [ 0.0284,  0.0035, -0.0250, -0.0029, -0.0068,  0.0098, -0.0174, -0.0049, -0.0243],
  [-0.0055,  0.0284,  0.0035, -0.0073, -0.0029, -0.0068, -0.0311,-0.0174, -0.0049]]]

如公式那样，将B加到QK得到的关系矩阵中。

attn = attn + relative_position_bias.unsqueeze(0)

Crossformer-Dynamic Position Bias

DPB也是相对位置编码的一种。但是其并不是从\widehat{B}中获取B的值，而是直接对相对位置进行编码。对于一个group_size=3的窗口，同样的，相对位置关系一共有25种，用代码表示为：

  1.     group_size = [3, 3]
  2.     position_bias_h = torch.arange(1 - group_size[0], group_size[0])
  3.     position_bias_w = torch.arange(1 - group_size[1], group_size[1])
  4.     biases = torch.stack(torch.meshgrid([position_bias_h, position_bias_w]))  # 2, 2Wh-1, 2W2-1
  5.     biases = biases.flatten(1).transpose(0, 1).float()
  6.     print(biases.shape)
  7.     print(biases)

torch.Size([25, 2])

[-2., -2.],[-2., -1.],[-2.,  0.],[-2.,  1.],[-2.,  2.],

[-1., -2.],[-1., -1.],[-1.,  0.],[-1.,  1.],[-1.,  2.],

[ 0., -2.],[ 0., -1.],[ 0.,  0.],[ 0.,  1.],[ 0.,  2.],

[ 1., -2.],[ 1., -1.],[ 1.,  0.],[ 1.,  1.],[ 1.,  2.],

[ 2., -2.],[ 2., -1.],[ 2.,  0.],[ 2.,  1.],[ 2.,  2.]

对以上相对位置通过一个可训练模块进行重新编码：

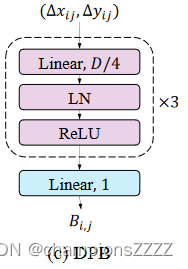
DPB 的结构如下图 所示。其非线性变换由三个全连接层组成，具有层归一化和 ReLU。 DPB的输入维度为2，即(Δxij，Δyij)，中间层的维度设置为D/4，其中D是嵌入的维度。输出 Bij 是一个标量，对第 i 个和第 j 个嵌入之间的相对位置特征进行编码。

 

  1. class DynamicPosBias(nn.Module):
  2.     def __init__(self, dim, num_heads, residual):
  3.         super().__init__()
  4.         self.residual = residual
  5.         self.num_heads = num_heads
  6.         self.pos_dim = dim // 4
  7.         self.pos_proj = nn.Linear(2, self.pos_dim)
  8.         self.pos1 = nn.Sequential(
  9.             nn.LayerNorm(self.pos_dim),
  10.             nn.ReLU(inplace=True),
  11.             nn.Linear(self.pos_dim, self.pos_dim),
  12.         )
  13.         self.pos2 = nn.Sequential(
  14.             nn.LayerNorm(self.pos_dim),
  15.             nn.ReLU(inplace=True),
  16.             nn.Linear(self.pos_dim, self.pos_dim)
  17.         )
  18.         self.pos3 = nn.Sequential(
  19.             nn.LayerNorm(self.pos_dim),
  20.             nn.ReLU(inplace=True),
  21.             nn.Linear(self.pos_dim, self.num_heads)
  22.         )
  23.     def forward(self, biases):
  24.         if self.residual:
  25.             pos = self.pos_proj(biases) # 2Wh-1 * 2Ww-1, heads
  26.             pos = pos + self.pos1(pos)
  27.             pos = pos + self.pos2(pos)
  28.             pos = self.pos3(pos)
  29.         else:
  30.             pos = self.pos3(self.pos2(self.pos1(self.pos_proj(biases))))
  31.         return pos

 将相对位置关系输入到该模块中，得到了类似于\widehat{B}的偏置矩阵。随后处理与SwinTSF相同。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/知新_RL/article/detail/371435
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号