跟着做DigitalOcean上的教程《使用TensorFlow构建神经网络来识别手写数字》

目标

跟着DigitalOcean上的教程《How To Build a Neural Network to Recognize Handwritten Digits with TensorFlow》中的步骤，学习使用TensorFlow构建一个能识别手写数字的神经网络。

注意：

• 原教程并非在Windows平台，而本篇是在Windows平台上测试。
• 原教程中的python版本与包版本在我本地配置的时候有问题，我已经换成了我本地实验可用的版本（细节详见附录）
• 做完后才发现，就算教程只是两年多前，但它所用的TensorFlow的API也已经落后当前最新太多了，用到的几乎所有的函数与对象都被警告已经被弃用。作为现在入门者而言可能会有些误导，毕竟最好从最新的接口开始学习。但是这篇我写都写完了，不发白不发（笑）。所以请多加注意。

第1步 - 配置项目

本篇将使用Python的3.7.9版本，并使用venv创建一个python的 虚拟环境(为了方便将此项目安装的包与你计算机中的其他项目隔离)。对此不熟悉的可以参考《学习使用venv创建“python虚拟环境”》。

首先创建一个空的文件夹，作为项目目录。我这里是 C:\tensorflow-demo

接着，在项目目录下创建一个requirements.txt文件用于指定所需的包：（注意此处包的版本和原教程不一样，详情见附录）

image==1.5.20
numpy==1.16.0
tensorflow==1.15
1
2
3

然后Cmd窗口中输入命令，在此目录创建虚拟环境

C:\Users\yaksue\AppData\Local\Programs\Python\Python37\python.exe -m venv C:\tensorflow-demo
1

然后，使用下面cmd命令激活这个虚拟环境：

C:\tensorflow-demo\Scripts\activate
1

进入后，先使用cd切换到这个项目路径

cd C:\tensorflow-demo
1

接着，就输入下面命令来安装requirements.txt文件中的包

pip install -r requirements.txt
1

安装好所需的包后，就可以正式开始了。

首先创建一个main.py用于放之后训练模型的脚本

第2步 - 导入MNIST数据集

本教程将使用的数据集称为MNIST数据集，它是机器学习社区的经典数据集。此数据集由手写数字图像组成，大小为 28x28 像素。以下是数据集中包含的一些数字示例：

---

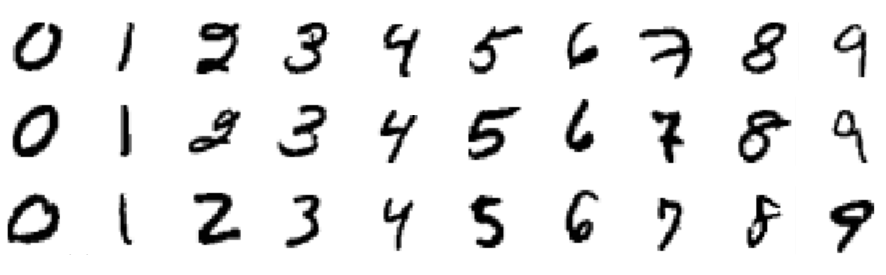
目前下载的tensorflow包里已经有针对于MNIST的数据结构，所以直接使用即可。
（我比较好奇这个数据结构在哪定义，所以我打印了它）

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

#测试打印下input_data在哪定义
print("print input_data： " + str(input_data))
1
2
3
4
5

在虚拟环境中运行python main.py后我看到：

print input_data： <module 'tensorflow.examples.tutorials.mnist.input_data' from 'C:\\tensorflow-demo\\lib\\site-packages\\tensorflow_core\\examples\\tutorials\\mnist\\input_data.py'>
1

---

接着，就可以用下面的脚本读取MNIST数据。
（为了验证是否读取成功，我打印了MNIST中：用于训练的样本数目、用于验证的样本数目、用于测试的样本数目）

#读取MNIST数据，如果本地还没有数据，则先下载
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)  # y labels are oh-encoded

n_train = mnist.train.num_examples
n_validation = mnist.validation.num_examples
n_test = mnist.test.num_examples
print("n_train: " + str(n_train))
print("n_validation: " + str(n_validation))
print("n_test: " + str(n_test))
1
2
3
4
5
6
7
8
9

注意：read_data_sets函数中的参数one_hot=True意思为 one-hot-encoding，表示使用二进制值向量来表示数值或分类值。比如我们的标签是数字 0-9，因此向量包含十个值，其中一个值设置为 1，表示向量中该索引处的数字，其余值设置为 0。例如，“3” 被表示为[0, 0, 0, 1, 0, 0, 0, 0, 0, 0]

一段时间后，可以看到输出：

n_train: 55000
n_validation: 5000
n_test: 10000
1
2
3

并且在本地可以看到 MNIST 数据刚刚被下载：

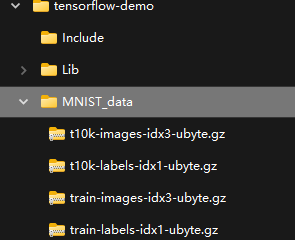
不用担心下次运行此脚本时又会下载一遍，因为看read_data_sets的逻辑，如果本地已存在则就不会下载了（可以再继续查，maybe_download在已有文件的情况下不会再次下载）：

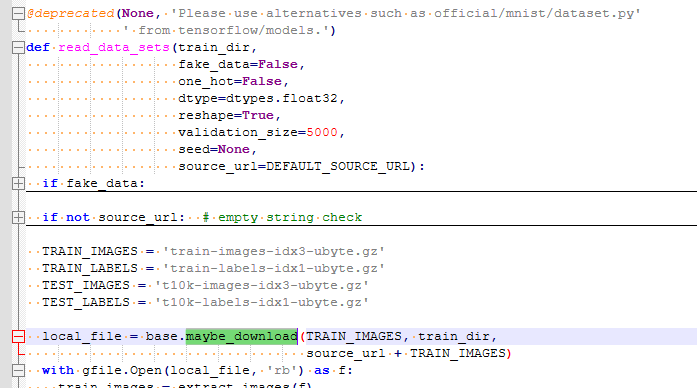
第3步 - 定义神经网络架构

“神经网络的架构” 指的是网络中的 “层数”、“每层单元数” 以及 “层间单元连接方式” 等。由于神经网络大致模仿人脑的工作原理，因此这里使用术语 “单元” 表示生物学上认为的 “神经元”。就像神经元在大脑中传递信号一样，“单元” 从 “先前的单元” 获取一些值作为输入，执行计算，然后将新值作为输出传递给 “其他单元”。这些单元的层级构成了网络，其中至少有一层用于输入值，还有一层用于输出值。术语 “隐藏层(hidden layer)” 用于表示 “输入层” 和 “输出层” 之间的所有层，即那些“对现实世界隐藏”的层。

“深度神经网络”中的“深度”一词与隐藏层的数量有关，“浅”通常表示只有一个隐藏层，“深”指多个隐藏层。

下面是我们的神经网络中的分层以及每层的单元数：

n_input = 784  # 输入层 (28x28像素)
n_hidden1 = 512  # 第一层隐藏层
n_hidden2 = 256  # 第二层隐藏层
n_hidden3 = 128  # 第三层隐藏层
n_output = 10  # 输出层 (0-9 数字)
1
2
3
4
5

用图形来表示我们的神经网络就是：

---

接下来，需要定义几个 超参数(hyperparameters)（指事先设置好的，学习过程中不会改变的参数。相对的，模型中的参数是会通过学习不断调整的）：

learning_rate = 1e-4#学习率
n_iterations = 1000 #迭代次数
batch_size = 128    #批次大小
dropout = 0.5       #随机失活
1
2
3
4

其中：

• learning_rate(学习率)表示在学习过程的每一步中，参数的调整程度。这些调整是训练的关键：每次通过网络后，我们都会稍微调整网络中的参数以尝试减少“损失”（“损失”指预测值与真实值之间的差异）
• n_iterations(迭代次数)是指我们进行训练步骤的次数。
• batch_size(批量大小)是指我们在每个步骤中使用的训练示例数量。
• dropout(随机失活)表示一个阈值，我们将使用这个阈值来随机消除某些单元。我们将在最后的隐藏层中使用它，这里使每个单元在每个训练步骤中都有 50% 的概率被消除。这有助于防止过拟合。

现在，我们已经定义了神经网络的架构以及影响学习过程的超参数。下一步是构建 TensorFlow 网络。

第4步 - 构建 TensorFlow 网络

我们需要建立一个TensorFlow可以用来执行的网络。TensorFlow 的核心概念是 tensor，它是一个类似于“数组”或“列表”的数据结构。在网络中传递时，tensor们被初始化和操作，并在学习过程中进行更新。

我们首先定义三个 tensors 作为 “占位符(placeholder)”，随后我们会将值输入到这些 tensors 中。

#输入
X = tf.placeholder("float", [None, n_input])
#输出
Y = tf.placeholder("float", [None, n_output])
#随机失活
keep_prob = tf.placeholder(tf.float32)
1
2
3
4
5
6

声明时，唯一需要指定的参数是我们将输入的数据的尺寸。对于X我们使用的结构为[None, 784]，其中None表示任意数量，因为我们将输入未知数量的图像，每个图像有 “784像素”。Y的形状为[None, 10]，因为我们将使用它来表示输出未知数量的标记，每个标记有 “10个可能的类别”。keep_prob 这个tensor用于控制 dropout，我们将其初始化为“placeholder”而不是“常量”，是因为我们希望在训练时（dropout设置为0.5）和测试时（dropout设置为1.0）使用相同的 tensor。

---

在训练过程中，weight和bias这两个参数会更新。因此需要为它们设置初始值，而不是空的placeholder。这些值本质上是神经网络进行学习的地方，因为它们用于神经元的 “激活函数(activation functions)”，表示单元之间的连接。

由于这些值在训练期间是不断优化的，所以将它们初始为零是可以的。但实际上，初始值对模型的最终准确性有重大影响。所以，对于weight 我们将使用一个 截断正态分布(truncated normal distribution) 的随机值。这样它们就接近零，却有正向或负向的轻微调整。

#对应于隐藏层1,2,3与输出层的weight，初始是个截断正态分布的随机值
weights = {
    'w1': tf.Variable(tf.truncated_normal([n_input, n_hidden1], stddev=0.1)),
    'w2': tf.Variable(tf.truncated_normal([n_hidden1, n_hidden2], stddev=0.1)),
    'w3': tf.Variable(tf.truncated_normal([n_hidden2, n_hidden3], stddev=0.1)),
    'out': tf.Variable(tf.truncated_normal([n_hidden3, n_output], stddev=0.1)),
}
1
2
3
4
5
6
7

对于bias，我们使用一个小的常数值来确保 tensor 在初始阶段激活。

#对应于隐藏层1,2,3与输出层的bias，初始是0.1
biases = {
    'b1': tf.Variable(tf.constant(0.1, shape=[n_hidden1])),
    'b2': tf.Variable(tf.constant(0.1, shape=[n_hidden2])),
    'b3': tf.Variable(tf.constant(0.1, shape=[n_hidden3])),
    'out': tf.Variable(tf.constant(0.1, shape=[n_output]))
}
1
2
3
4
5
6
7

---

接下来，通过定义对 tensor 进行的操作来建立层。

#隐藏层1 = 输入*w1+b1
layer_1 = tf.add(tf.matmul(X, weights['w1']), biases['b1'])
#隐藏层2 = 隐藏层1*w2+b2
layer_2 = tf.add(tf.matmul(layer_1, weights['w2']), biases['b2'])
#隐藏层3 = 隐藏层2*w3+b3
layer_3 = tf.add(tf.matmul(layer_2, weights['w3']), biases['b3'])
#随机失活
tf.nn.dropout(layer_3, keep_prob)
#输出层 = 隐藏层3*w_out+b_out
output_layer = tf.matmul(layer_3, weights['out']) + biases['out']
1
2
3
4
5
6
7
8
9
10

每个隐藏层将对前一层的输出和当前层的weights执行矩阵乘法，并添加biases。（即 $\times weight+bias$）

在最后一个隐藏层，将使用keep_prob这个阈值做随机失活。

---

构建网络的最后一步是定义 损失函数(loss function)。

损失函数用于衡量 “预测值” 与 “真实值” 之间的差异。

TensorFlow 中一种常用的损失函数是 “交叉熵(cross-entropy)”，也称为 “对数损失(log-loss)”。

我们还需要选择用于最小化损失函数的优化算法。“梯度下降优化(gradient descent optimization)”是一种常见的方法，通过沿着梯度的负方向（下降方向）进行迭代，来找到函数的（局部）最小值。TensorFlow 中已经实现了几种梯度下降优化算法，在本教程中我们将使用 Adam Optimizer。

#损失函数
cross_entropy = tf.reduce_mean(
    tf.nn.softmax_cross_entropy_with_logits(
        labels=Y, logits=output_layer
        ))

#梯度下降优化
train_step = tf.train.AdamOptimizer(learning_rate).minimize(cross_entropy)
1
2
3
4
5
6
7
8

现在我们已经定义了网络，并使用 TensorFlow 构建了它。下一步是通过对网络输入数据来训练它，然后测试它是否真的学到了一些东西。

第5步 - 训练 & 使用测试样本来评判准确度

训练过程包括 “将训练数据集输入到网络中” 并 “不断优化损失函数”。每迭代一批训练样本，它都会更新参数以减少损失，以便更准确地预测显示的数字。

测试过程包括用训练好的网络运行我们的测试数据集，根据正确预测的图像数量来计算准确率。

在开始训练过程之前，我们将定义用于评估“准确度”的方法，以便在训练时将其打印到每个批次上。这些打印的信息将使我们能够检查从第一次迭代到最后一次，损失是否在减少，准确性是否在提高；它们还将使我们能够看到我们是否进行了足够的迭代次数以达到一致和最优的结果。

#用于评估准确度的方法
correct_pred = tf.equal(tf.argmax(output_layer, 1), tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))
1
2
3

在correct_pred中，我们使用argmax函数通过查看output_layer(预测) 和 Y(标签) 来比较哪些图像被正确预测，然后使用equal函数将其作为“布尔值列表”返回。然后我们可以将此列表转换为浮点数并计算 平均值（mean）以获得总体准确度分数。

---

现在，我们已准备好初始化一个 session 来运行该网络。在此 session 中，我们将向网络提供训练样本。训练完成后，我们将向同一网络提供新的测试样本来评判模型的准确性。

#创建一个TensorFlow的session
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
1
2
3
4

训练过程的本质是优化损失函数。我们的目标是让预测标记与真实标记之间的差异最小化。该过程涉及四个步骤，重复一定次数的迭代：

• 通过网络传递值
• 计算损失
• 通过网络向后传递值
• 更新参数

在每个训练步骤中，都会对参数进行轻微调整，以尝试减少下一步的损失。随着学习的进行，我们应该看到损失不断减少，最终我们可以停止训练并使用该网络作为测试新数据的模型。

#训练：
for i in range(n_iterations):
    batch_x, batch_y = mnist.train.next_batch(batch_size)
    sess.run(train_step, feed_dict={
        X: batch_x, Y: batch_y, keep_prob: dropout
        })

    #每100迭代打印一次准确度
    if i % 100 == 0:
        minibatch_loss, minibatch_accuracy = sess.run(
            [cross_entropy, accuracy],
            feed_dict={X: batch_x, Y: batch_y, keep_prob: 1.0}
            )
        print(
            "Iteration",
            str(i),
            "\t| Loss =",
            str(minibatch_loss),
            "\t| Accuracy =",
            str(minibatch_accuracy)
            )
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

---

训练完成后，我们可以在测试图像上运行 session。这次我们让keep_prob为1.0确保所有单元在测试过程中都处于活动状态。

#对于测试集进行测试
test_accuracy = sess.run(accuracy, feed_dict={X: mnist.test.images, Y: mnist.test.labels, keep_prob: 1.0})
print("\nAccuracy on test set:", test_accuracy)
1
2
3

---

现在，可以运行下main.py查看结果了。在cmd中输入python main.py：
得到输出：

Iteration 0     | Loss = 4.3634033      | Accuracy = 0.046875
Iteration 100   | Loss = 0.44375277     | Accuracy = 0.859375
Iteration 200   | Loss = 0.4945774      | Accuracy = 0.8671875
Iteration 300   | Loss = 0.5085759      | Accuracy = 0.875
Iteration 400   | Loss = 0.32885414     | Accuracy = 0.90625
Iteration 500   | Loss = 0.25877178     | Accuracy = 0.9296875
Iteration 600   | Loss = 0.32915002     | Accuracy = 0.9375
Iteration 700   | Loss = 0.44877478     | Accuracy = 0.890625
Iteration 800   | Loss = 0.31691086     | Accuracy = 0.90625
Iteration 900   | Loss = 0.30365703     | Accuracy = 0.90625

Accuracy on test set: 0.9182
1
2
3
4
5
6
7
8
9
10
11
12

第6步 - 使用自己的手写数据进行测试

首先我下载了这个教程里提供的用于测试的图片，然后自己手写了三个数字，合计四个样本：

脚本上，为了能读取图片，要再import两个库，将下面两行添加到脚本顶端：

import numpy as np
from PIL import Image
1
2

接下来定义一个函数用于对本地的图片进行预测：

#定义一个函数用于对本地的图片进行预测
def test_predict(img_path):
    img = np.invert(Image.open(img_path).convert('L')).ravel()
    prediction = sess.run(tf.argmax(output_layer, 1), feed_dict={X: [img]})
    print ("Prediction for "+img_path+" :", np.squeeze(prediction))
1
2
3
4
5

然后对四个图片进行预测：

#测试：
test_predict("mytest0.png")
test_predict("mytest1.png")
test_predict("mytest2.png")
test_predict("mytest3.png")
1
2
3
4
5

不过结果有点失望，教程给的图片预测对了，但是我自己手写的只预测对了1个：（不知道是否是我写的图片的样式和MNIST中的有较大差别）

Prediction for mytest0.png : 2
Prediction for mytest1.png : 3
Prediction for mytest2.png : 5
Prediction for mytest3.png : 6
1
2
3
4

完整的main.py

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import numpy as np
from PIL import Image

#测试打印下input_data在哪定义
print("print input_data： " + str(input_data))

#读取MNIST数据，如果本地还没有数据，则先下载
mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)  # y labels are oh-encoded

n_train = mnist.train.num_examples
n_validation = mnist.validation.num_examples
n_test = mnist.test.num_examples
print("n_train: " + str(n_train))
print("n_validation: " + str(n_validation))
print("n_test: " + str(n_test))

#神经网络结构：
n_input = 784  # 输入层 (28x28像素)
n_hidden1 = 512  # 第一层隐藏层
n_hidden2 = 256  # 第二层隐藏层
n_hidden3 = 128  # 第三层隐藏层
n_output = 10  # 输出层 (0-9 数字)

#定义超参数：
learning_rate = 1e-4#学习率
n_iterations = 1000 #迭代次数
batch_size = 128    #批次大小
dropout = 0.5       #随机失活

#输入
X = tf.placeholder("float", [None, n_input])
#输出
Y = tf.placeholder("float", [None, n_output])
#随机失活
keep_prob = tf.placeholder(tf.float32)

#对应于隐藏层1,2,3与输出层的weight，初始是个截断正态分布的随机值
weights = {
    'w1': tf.Variable(tf.truncated_normal([n_input, n_hidden1], stddev=0.1)),
    'w2': tf.Variable(tf.truncated_normal([n_hidden1, n_hidden2], stddev=0.1)),
    'w3': tf.Variable(tf.truncated_normal([n_hidden2, n_hidden3], stddev=0.1)),
    'out': tf.Variable(tf.truncated_normal([n_hidden3, n_output], stddev=0.1)),
}

#对应于隐藏层1,2,3与输出层的bias，初始是0.1
biases = {
    'b1': tf.Variable(tf.constant(0.1, shape=[n_hidden1])),
    'b2': tf.Variable(tf.constant(0.1, shape=[n_hidden2])),
    'b3': tf.Variable(tf.constant(0.1, shape=[n_hidden3])),
    'out': tf.Variable(tf.constant(0.1, shape=[n_output]))
}

#隐藏层1 = 输入*w1+b1
layer_1 = tf.add(tf.matmul(X, weights['w1']), biases['b1'])
#隐藏层2 = 隐藏层1*w2+b2
layer_2 = tf.add(tf.matmul(layer_1, weights['w2']), biases['b2'])
#隐藏层3 = 隐藏层2*w3+b3
layer_3 = tf.add(tf.matmul(layer_2, weights['w3']), biases['b3'])
#随机失活
tf.nn.dropout(layer_3, keep_prob)
#输出层 = 隐藏层3*w_out+b_out
output_layer = tf.matmul(layer_3, weights['out']) + biases['out']

#损失函数
cross_entropy = tf.reduce_mean(
    tf.nn.softmax_cross_entropy_with_logits(
        labels=Y, logits=output_layer
        ))

#梯度下降优化
train_step = tf.train.AdamOptimizer(learning_rate).minimize(cross_entropy)

#用于评估准确度的方法
correct_pred = tf.equal(tf.argmax(output_layer, 1), tf.argmax(Y, 1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))

#创建一个TensorFlow的session
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)

#训练：
for i in range(n_iterations):
    batch_x, batch_y = mnist.train.next_batch(batch_size)
    sess.run(train_step, feed_dict={
        X: batch_x, Y: batch_y, keep_prob: dropout
        })

    #每100迭代打印一次准确度
    if i % 100 == 0:
        minibatch_loss, minibatch_accuracy = sess.run(
            [cross_entropy, accuracy],
            feed_dict={X: batch_x, Y: batch_y, keep_prob: 1.0}
            )
        print(
            "Iteration",
            str(i),
            "\t| Loss =",
            str(minibatch_loss),
            "\t| Accuracy =",
            str(minibatch_accuracy)
            )

#对于测试集进行测试
test_accuracy = sess.run(accuracy, feed_dict={X: mnist.test.images, Y: mnist.test.labels, keep_prob: 1.0})
print("\nAccuracy on test set:", test_accuracy)

#-----下面测试本地的图片-----

#定义一个函数用于对本地的图片进行预测
def test_predict(img_path):
    img = np.invert(Image.open(img_path).convert('L')).ravel()
    prediction = sess.run(tf.argmax(output_layer, 1), feed_dict={X: [img]})
    print ("Prediction for "+img_path+" :", np.squeeze(prediction))

#测试：
test_predict("mytest0.png")
test_predict("mytest1.png")
test_predict("mytest2.png")
test_predict("mytest3.png")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122

附录

1. 配置时包的版本问题

按照原教程来安装包，会报protobuf这个包并不支持3.6版本：

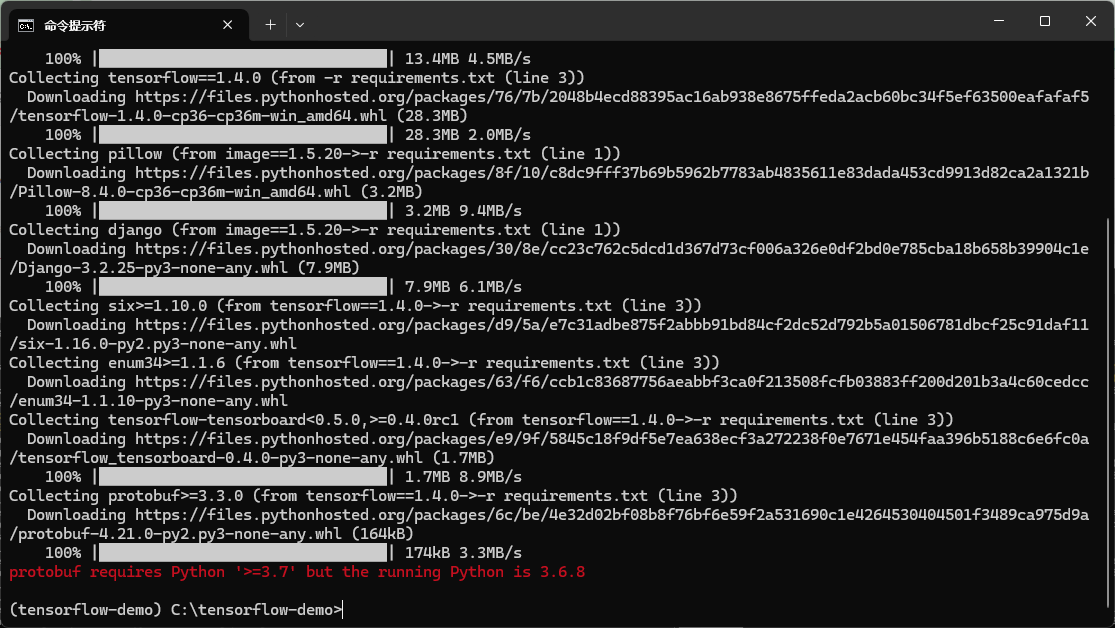
接着，换成3.7，又报 TensorFlow的版本没找到：

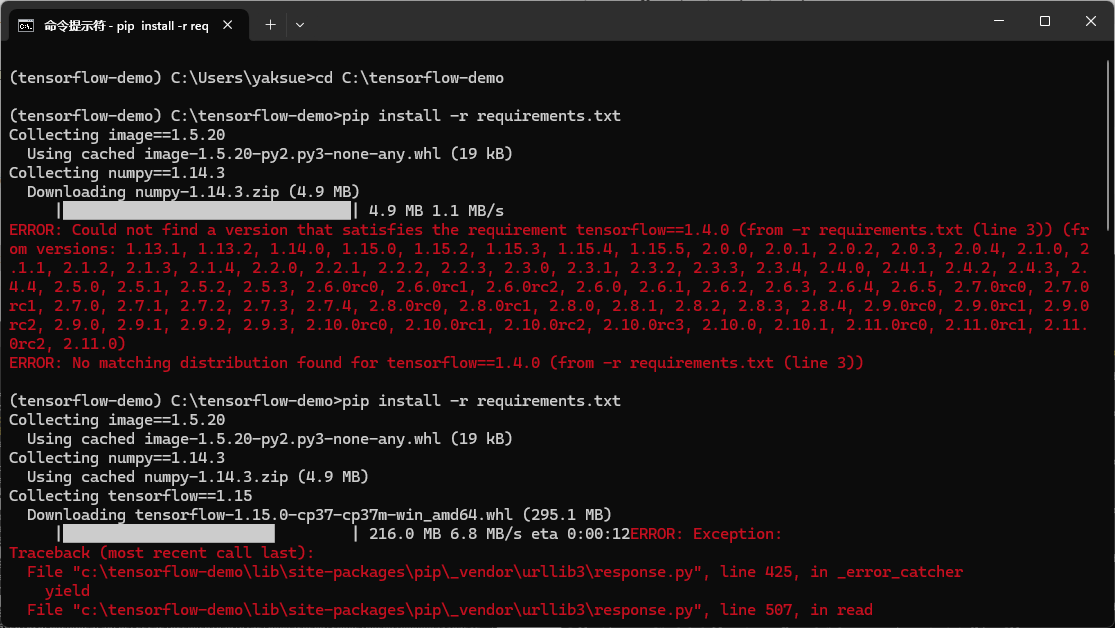
所以最后，我选择了 TensorFlow 1版的最终版即1.15.
接着还遇到个问题，就是下载的时候有报错：

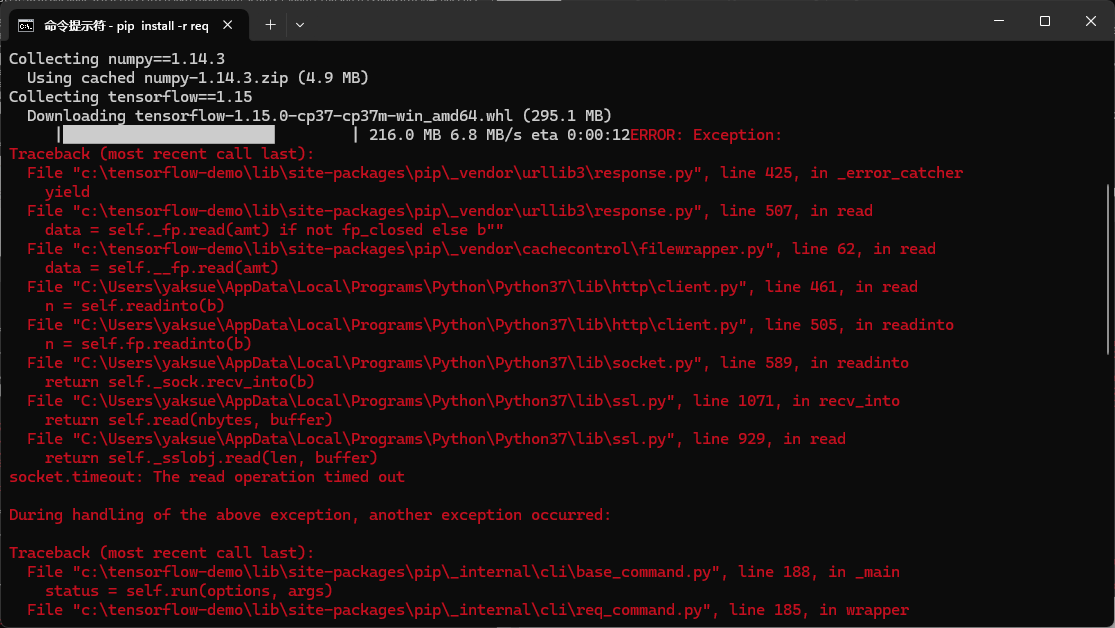
但上面的问题应该是偶然的，我再次运行后就没有遇到了。
但之后，又遇到问题是报numpy版本不对

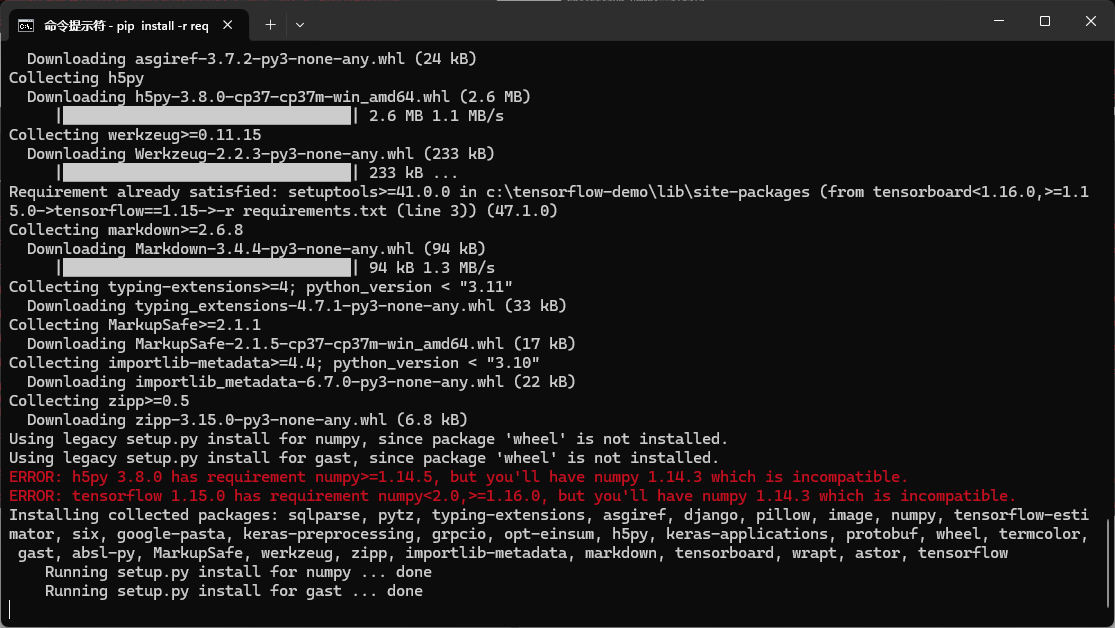
所以最终numpy也换成了1.16.0
至此，在配置阶段没有再报有关包的问题了。

2. protobuf 版本问题

在import tensorflow 后，遇到报错：

根据这里的方案。
可以安装个更低的版本

pip uninstall protobuf # 首先先卸载protobuf
pip install protobuf==3.20.1 # 重新安装一个 提示所建议的版本号 3.20.x 
1
2

测试后管用。