算法入门介绍

简单梳理下什么是算法，为什么要研究算法、如果研究算法。

什么是算法

非形式地说，算法(Algorithm)是任何良定义的计算过程。科学地说，算法是一系列解决问题的明确指令，也就是说，对于符合一定规范的输入，能够在有限时间内获得要求的输出。图形表示如下：

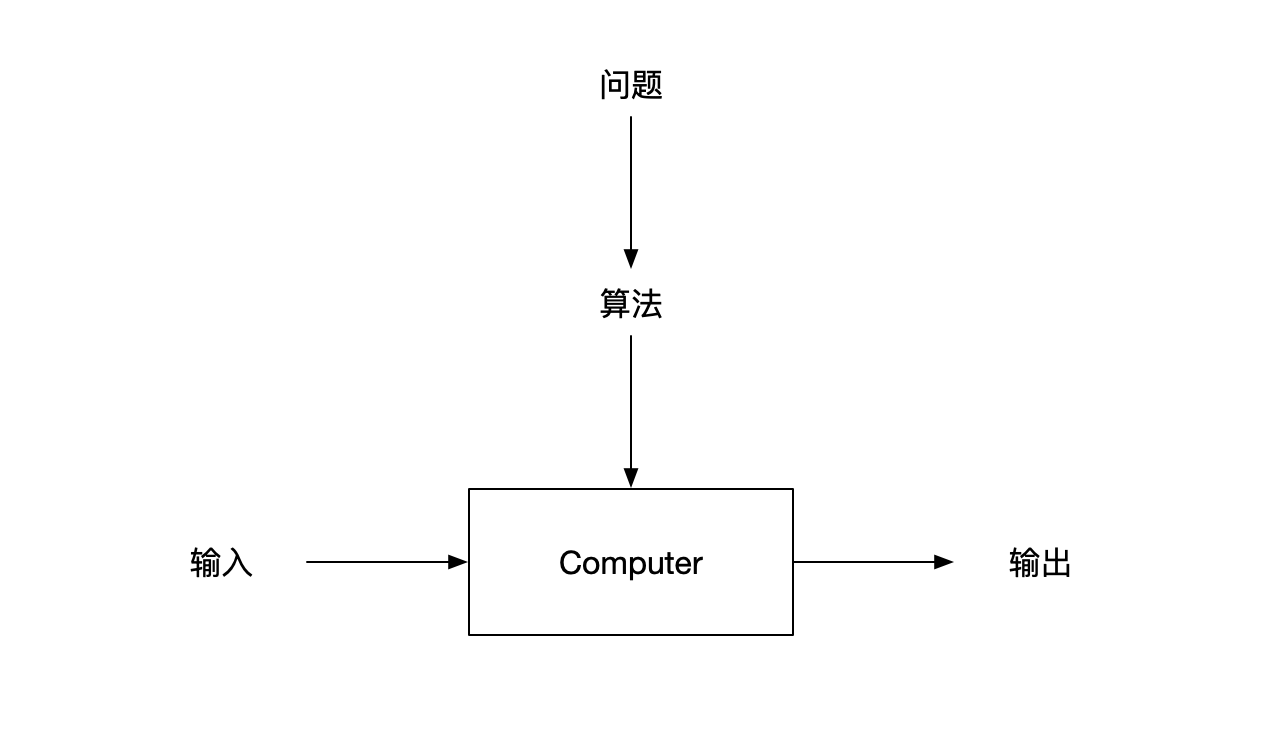
可以将算法看成是用于求解良说明的计算问题的工具。一般来说，问题陈述说明了期望的输入/输出关系，算法则描述一个特定的计算过程来实现该输入/输出关系。

为什么要研究算法

算法是计算机科学的一个分支。它是计算机科学的核心。作为计算机专业人士，无论从实践的角度，还是从理论的角度，学习算法是必需的。从实践的角度，学习算法有助于我们解决开发实践过程中遇到的问题。此外，还能帮助设计新算法，提高算法效率。从理论的角度，算法是计算机科学的基石。
尽管计算机可以运行的很快(普通cpu的执行速度也可达2GHz，即每秒执行2亿次)，但它不是无限快。存储器也许是廉价的，但它不是免费的。所以计算时间是一种有效资源，存储空间也一样。所以，研究算法仍有必要。

如何设计和分析算法

既然算法如此重要，又该如何设计和分析算法呢？一般来说，算法设计和分析经历一系列典型步骤，如下图所示：

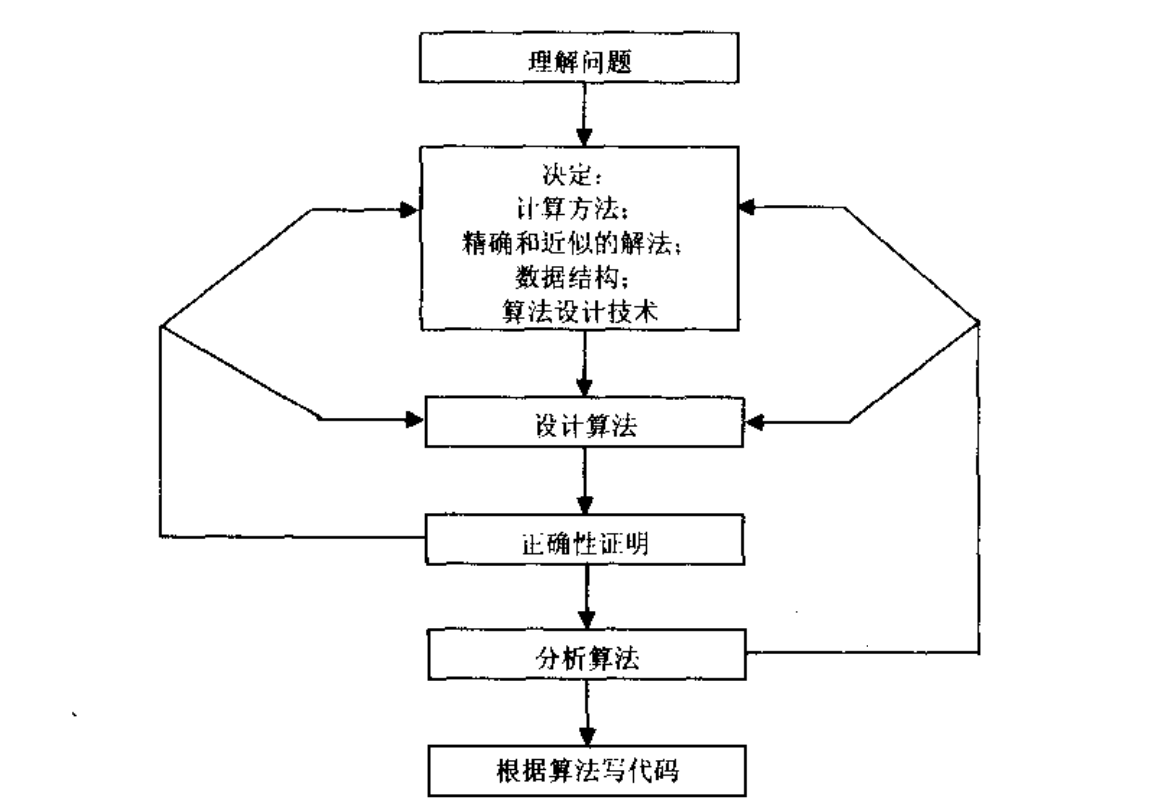
理解问题

在设计算法前，我们首先需要对给定的问题有完全的理解。试着从问题的实例入手是一个不错的选择。
算法的输入，确定了该算法所解问题的一个实例。严格确定算法需要处理的实例的范围是很有必要的。因为不同的输入规模，可能会带来算法的不同。同时，算法对“边界值”也应适用。正确的算法不仅应能处理大多数常见情况，而且应该能正确处理所有合法的输入。
所以，不应在未完全弄清楚问题前，就展开算法设计，否则会带来不必要的重复。

了解计算设备的性能

理解待处理的问题，还需搞清楚将要运行算法的设备的性能。类冯-诺依曼体系仍是计算机的主流，所以大多数算法的代码运行在该种体系结构下。冯-诺依曼体系结构的根本在于随机存取(Random-Access Machine, RAM)，在这种体系结构最主要的假设是，指令逐条执行，每次执行一步操作。相应的，设计在这种机器上运行的算法称为顺序算法(Sequential Algorithm)。
一些新式计算机打破了RAM模型的假设，它们可以同一时间执行多条操作，即并行计算。能够利用这种计算能力的算法称为并行算法(Parallel Algorithm)。因为冯-诺依曼体系已经成为现行的事实标准，所有该种结构下的算法仍将主导很长一段时间。

在精确算法和近似算法之间做出选择

接下来，设计算法前要明确是精确求解，还是近似求解。为什么有时要选择近似算法？首先，一些重要问题无法得到精确解。如求平方根、解非线性方程、求定积分等。其次，由于某些问题固有的复杂性，用已知的精确解法求解的性能不尽如人意。最后，一个近似解法可以作为更复杂的精确算法的一部分。

算法的设计技术

现在，可以考虑设计一个算法来解决给定的问题了。算法设计可遵循一定的方法论。我们可以通过学习一些基础问题的算法设计，帮助提高算法设计能力。这是一个能力提升的过程。

确定适当的数据结构

尽管算法设计技术提供了一套通用的方法来对问题算法求解，但为特定问题设计算法仍是一项具有挑战性的任务。
当然，设计人员需要根据算法执行的操作选择合适的数据结构，不同的数据结构对应不同的操作，其算法也有差异。如需要随机读取集合中的元素，此时选择数组的算法效率要高于选用链表。

算法的描述

设计好算法后（对问题有解题思路后），就需要按照一定的方式对它进行详细描述。如使用自然语言描述算法，或使用伪代码描述算法。
使用自然语言描述算法是最直接方式。然而，这种方式会因自然语言固有的不严密性，使得描述存在歧义，且无法简单清晰的描述算法。
伪代码(pseudocode)是自然语言和类编程语言组成的混合结构。伪代码比自然语言更精确，且更能以简洁的方式描述算法。
注意，伪代码的编写无统一规范，但从经验来看，熟悉现代编程语言的人，都能对伪代码理解。
在计算机应用早期，描述算法的主要工具是流程图(Flow Chart)。流程图使用一系列相连的几何图形来描述算法。实践证明，这种表示使用起来非常不方便。
当代计算机技术还不能将自然语言或伪代码描述的算法直接“注入”计算机。我们还需要把算法变成用特定编程语言编写的程序。

算法的正确性证明

一旦完成对算法的描述，接下来就必须证明它的正确性。也就是说，我们必须证明对于每一个合法输入，该算法都能在有限的时间内输出一个需要的结果。
对于某些算法来说，正确性的证明是十分简单的；而对于另一些算法，却可能是十分复杂的。
对近似算法的正确性定义则没有精确算法那么直接。对于一个近似算法，常试图证明该算法所产生的误差不超过预定义的范围。

算法的分析

除了算法的正确性，算法最重要的特就是效率(Efficiency)了。有两种算法效率：时间效率(Time Efficiency)和空间效率(Space Effiency)。其中时间效率指出算法那运行有多快，空间效率说明算法需要多少额外的空间。
算法的另一个特性就是简单性(Simplicity)。效率可以用数学的严密性进行精确的定义和研究证明，而简单性就像"美"一样，很大程度取决于审视者的眼光。
简单的算法，更容易理解和实现，因而也更容易维护。有时，简单算法的效率比复杂算法效率更高。实际应用中，还需进行谨慎的权衡。
我们希望拥有的另一个算法特性是一般性(Generality，通用性)。这里包含两层含义：算法所解决问题的一般性和算法可接受输入的一般性。有些情况下，考虑一般性，可以帮助我们设计更优的算法，但是有些情况下，则会使问题更加难以解决。
如果我们对算法的效率、简单性或一般性不满意，则必须重新设计算法。其实，即使我们对算法做出了肯定评价，也有必要去探寻另一种算法。一般来说，不要指望依靠一次尝试就能找到最好的算法。

算法对应代码编写

大部分算法最终以计算机程序的形式实现。为算法编程既是挑战，也是机遇。
现实中，迫使我们停止算法优化的，往往是项目进度表和老板的耐心。完美的代价往往是高昂的，而且并不总是提倡的。设计算法是一种工程行为，需要在资源有限的情况下，在互斥的目标做权衡，设计者的时间就是这样一种资源。

实例

接下来，将从实例入手，简单介绍下如何实现算法的设计与分析。

求最大公约数问题

问题描述

最大公约数（Greatest Common Divisor）指两个或多个整数共有约数中最大的一个。也称最大公因数、最大公因子，以两个数a，b为例，两个数的最大公约数可记为gcd(a,b)。

算法设计

理解待处理的问题，还需搞清楚将要运行算法的设备的性能。由于代码运行的平台主要是类冯-诺依曼体系，所以不对设备进行区分。由于该问题是求最大公约数，而最大公约数只有一个。所以该问题应使用精确算法求解。对于同一问题，其解决方法可能有多个。该题就存在多种解法，对应的算法设计也是多种。如连续整数检测法、欧几里得法、质因数分解法等，下面将一一介绍。

1. 连续整数检测法

两个数的最大公约数就是能够同时整除这两个数的最大正整数。显然，公约数的最小值是1。(1可以整除任何正整数)，公约数的最大值一定不会小于两个数中较小的那个。所以，可以遍历1到较小数，能同时整数两个数的最大值，就是最大公约数。可以看到，这种方法是穷举法的一种应用。伪代码表示如下：

t = min{m,n}
for i=t to 1 do
    if(m MOD i == 0 && n MOD i == 0){
        return i;
    }
    i--
1
2
3
4
5
6

对于上述循环，因为i为1时，必能同时整除m和n，所以该循环必能结束。

2. 欧几里得法

欧几里得算法（Euclidean algorithm），又叫辗转相除算法。它是已知最古老的算法,其可追溯至公元前300年前。欧几里得算法基于一个定理：两个正整数 x 和 y（x 大于 y）,它们的最大公约数等于 x 除以 y 的余数 z 和 较小数 y 之间的最大公约数。公式表示为$gcd(x,y)=gcd(y,xMODy)$。该算法的伪代码表示如下：

while y != 0 do
    z = x MOD y
    x = y;
    y = z;
return a;
1
2
3
4
5

因为b单调递减，且其最小值为1，所以while循环必能结束。

3. 质因数分解法

质因数分解法，就是先求出两个数的质因数，然后找出所有的公因数，这些公因数的乘积就是最大公约数。举例来说，对于60和24这两个数，质因数分解后：

60 = 2✖️2✖️3✖️5
24 = 2✖2✖️2✖️3
gcd(60,24) = 2✖2✖️3 = 12
1
2
3

该算法的描述如下：

第一步：找到m的所有质因数
第二步：找到n的所有质因数
第三步：从第一步和第二步的质因数分解式中找出所有的公因数
第四步：将第三步中找到的质因数相乘，其结果作为两个数的最大公约数  
1
2
3
4

需要说明的是，上述算法虽然很简洁，但是从编码实现角度来说，如何对一个数质因数分解是个问题。接下来将介绍一个算法，用来产生一个不大于给定整数n的连续质数序列。这个算法称为"埃拉托色尼筛选法(Sieve of Eratosthenes)"。该算法一开始初始化一个2~n的连续整数序列，作为候选质数(排除1，1不是质数)。然后，将2的倍数从序列中消去。然后是3，以此类推。该算法会一直循环下去，直到序列中没有可消的元素为止。
埃拉托色尼筛选法的实现，有兴趣的同学可以参考这篇博客。

算法代码编写

由于该算法实现很简单，不需要对数据结构进行选择或设计，算法的描述在上一小节已完成。算法的正确性，虽然没有经过严谨的证明，但根据已有的数学知识，其正确性还是可以保证的。更严谨的数学证明，这里就不展开说了，有兴趣的同学，可以自行补充完善。算法代码的编写。这里只完成了连续整数检测法和欧几里得法，质因数分解法可参考上面的博客链接。

参考

《算法导论》第三版 Tomas H. Cormen etc. 殷建平 等译
《算法设计与分析基础》 第三版 Anany Levitin 著 潘彦 译
https://blog.csdn.net/qq_41575507/article/details/90752742 求最大公约数
https://blog.csdn.net/NGU_Jq/article/details/84311112 辗转相除求最大公约数
https://www.cnblogs.com/liuzhen1995/p/6234972.html 算法笔记_012:埃拉托色尼筛选法

原创不易，如果本文对您有帮助，欢迎关注我，谢谢 ~_~