Leetcode刷题方法总结---链表全解_leecode 刷题链表
赞
踩
Leetcode刷题方法总结—链表全解
链表基本知识回忆
详细知识可以看我的:数据结构专栏
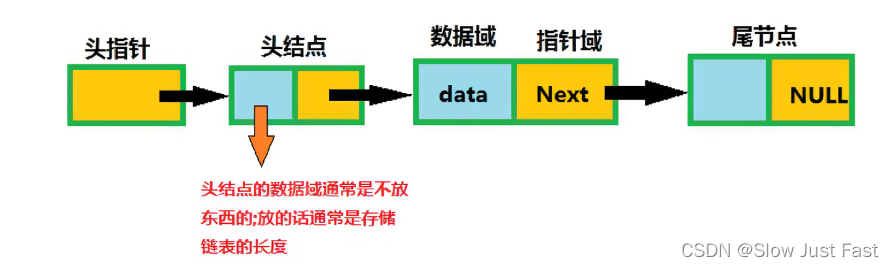
什么是链表?—链表是一种通过指针串联在一起的线性结构,每一个节点由两部分组成,一个是数据域一个是指针域(存放指向下一个节点的指针),最后一个节点的指针域指向null(空指针的意思),链接的入口节点称为链表的头结点也就是head
单链表:如下图—单链表中的指针域只能指向节点的下一个节点
双链表:每一个节点有两个指针域,一个指向下一个节点,一个指向上一个节点,双链表 既可以向前查询也可以向后查询
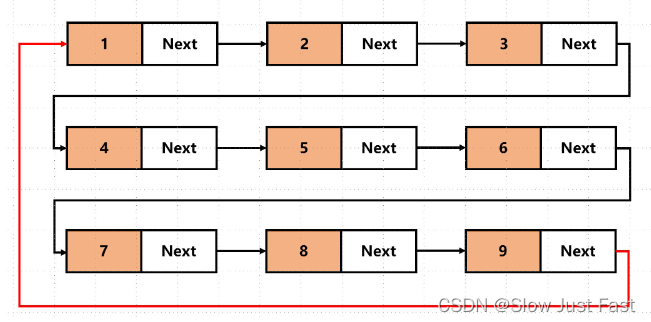
循环链表:顾名思义,就是链表首尾相连,循环链表可以用来解决约瑟夫环问题
链表存储方式:是通过指针域的指针链接在内存中各个节点,所以链表中的节点在内存中不是连续分布的 ,而是散乱分布在内存中的某地址上,分配机制取决于操作系统的内存管理
题型一:移除链表元素
举例Leetcode题目 移除链表元素:题目地址
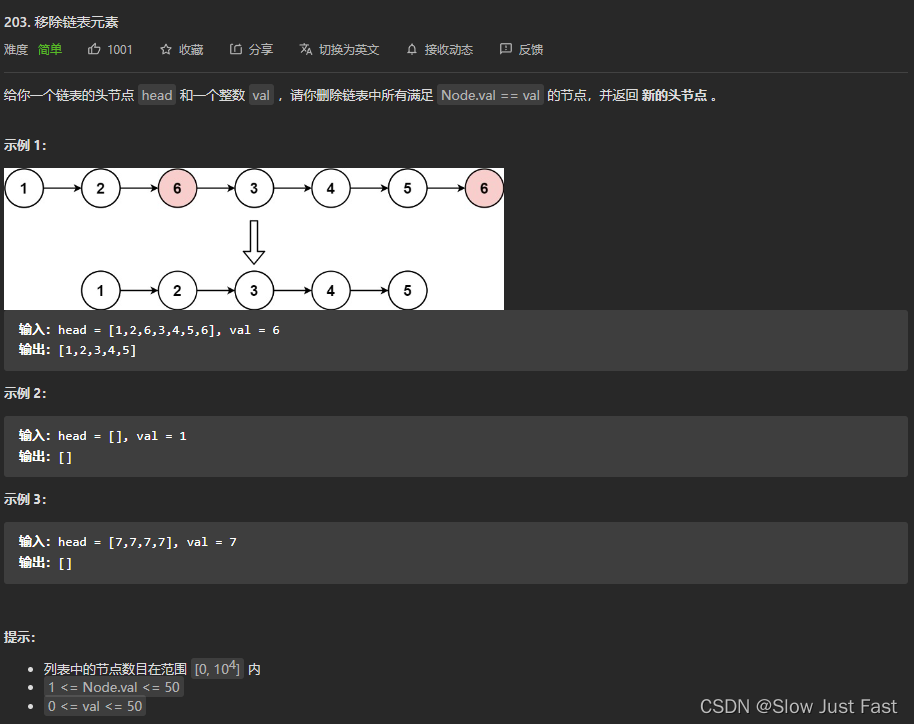
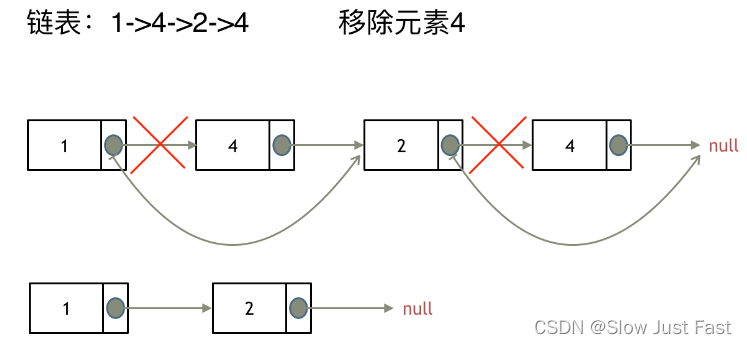
思路:直接让被删除元素没有被next指向就行了
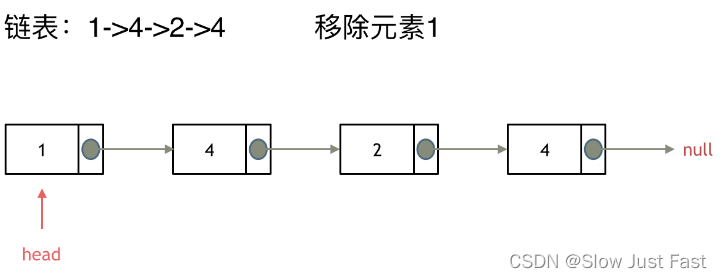
这里以链表 1 4 2 4 来举例,移除元素4
如果使用C,C++编程语言的话,不要忘了还要从内存中删除这两个移除的节点,如果使用java ,python的话就不用手动管理内存了
链表操作的两种方式:直接使用原来的链表来进行删除操作(不推荐使用,相对代码不统一)、设置一个虚拟头结点在进行删除操作(推荐,相对代码统一)
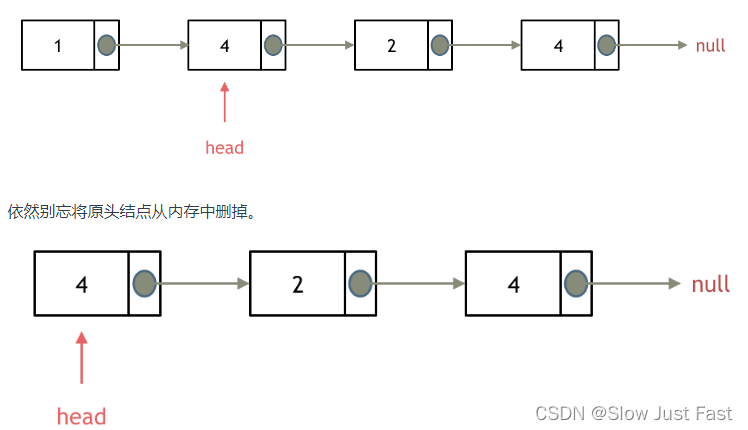
方法一:直接使用原来的链表进行删除操作
移除头结点和移除其他节点的操作是不一样的,因为链表的其他节点都是通过前一个节点来移除当前节点,而头结点没有前一个节点,所以头结点如何移除呢,其实只要将头结点向后移动一位就可以,这样就从链表中移除了一个头结点
方法二:设置一个虚拟头结点在进行删除操作
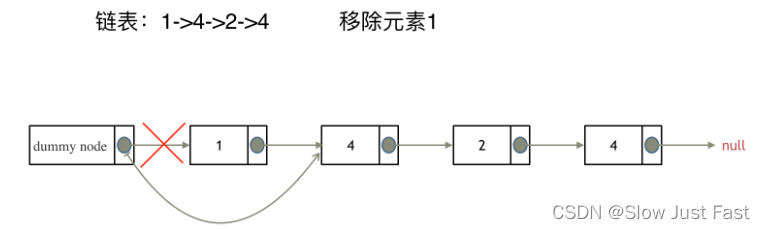
设置一个虚拟头结点(dummy node,也有很多课本直接叫的空head),这样原链表的所有节点就都可以按照统一的方式进行移除了
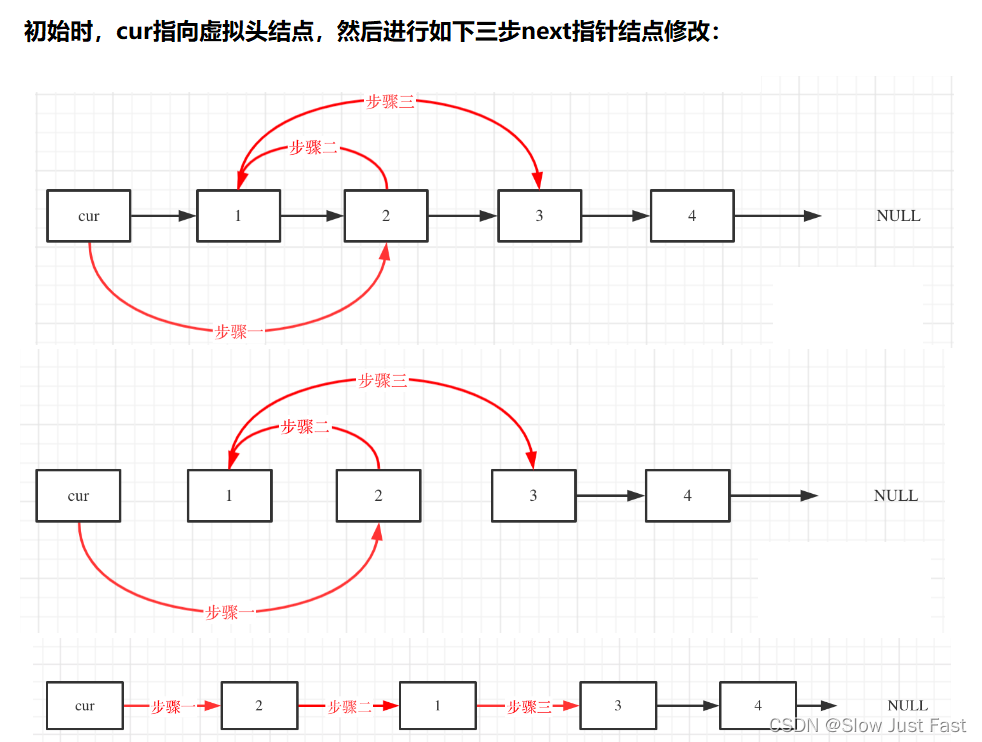
这里来给链表添加一个虚拟头结点为新的头结点,此时要移除这个旧头结点元素1。
这样是不是就可以使用和移除链表其他节点的方式统一了呢?
来看一下,如何移除元素1 呢,还是熟悉的方式,然后从内存中删除元素1。
最后呢在题目中,return 头结点的时候,别忘了
return dummyNode->next;, 这才是新的头结点(虚拟头节点不要算作头结点)
class Solution { public: ListNode* removeElements(ListNode* head, int val) { //方法一:直接使用原来的链表进行删除操作 // 删除头结点---删除满足条件的val while (head != NULL && head->val == val)//先判断head是不是空,否则head->val可能会报错 { // 注意这里不是if,考虑有几个要删除的排在一起 ListNode* tmp = head; head = head->next; delete tmp; } // 删除非头结点 ListNode* cur = head; while (cur != NULL && cur->next!= NULL) { if (cur->next->val == val) { ListNode* tmp = cur->next; cur->next = cur->next->next; delete tmp; } else { cur = cur->next; } } return head; } }; //推荐方法二:有虚拟头结点很多操作会方便的多 class Solution { public: ListNode* removeElements(ListNode* head, int val) { //方法二:设置一个虚拟头结点在进行删除操作 ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点 dummyHead->next = head; // 将虚拟头结点指向head,这样方面后面做删除操作 ListNode* cur = dummyHead;//cur用来遍历结点 while (cur->next != NULL) { if(cur->next->val == val) { ListNode* tmp = cur->next; cur->next = cur->next->next; delete tmp; } else { cur = cur->next; } } head = dummyHead->next; delete dummyHead; return head; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
题型二:完善链表设计
链表设计类型的题目其实就是让我们把链表的基本功能给写出来,考察我们对于链表的掌握和对于实际不同需求的灵活处理
举例Leetcode题目 设计链表:题目地址
class MyLinkedList { public: // 定义链表节点结构体 struct LinkedNode { int val; LinkedNode* next; LinkedNode(int val):val(val), next(nullptr){} }; // 初始化链表 MyLinkedList() { _dummyHead = new LinkedNode(0); // 这里定义的头结点 是一个虚拟头结点,而不是真正的链表头结点 _size = 0; } // 获取到第index个节点数值,如果index是非法数值直接返回-1, 注意index是从0开始的,第0个节点就是头结点 int get(int index) { if (index > (_size - 1) || index < 0) { return -1; } LinkedNode* cur = _dummyHead->next; while(index--)//通过递减index从而递增cur指针去遍历到需要返回的结点 { // 如果--index 就会陷入死循环 cur = cur->next; } return cur->val; } // 在链表最前面插入一个节点,插入完成后,新插入的节点为链表的新的头结点 void addAtHead(int val) { LinkedNode* newNode = new LinkedNode(val); newNode->next = _dummyHead->next; _dummyHead->next = newNode; _size++; } // 在链表最后面添加一个节点 void addAtTail(int val) { LinkedNode* newNode = new LinkedNode(val); LinkedNode* cur = _dummyHead; while(cur->next != nullptr) { cur = cur->next; } cur->next = newNode; _size++; } // 在第index个节点之前插入一个新节点,例如index为0,那么新插入的节点为链表的新头节点。 // 如果index 等于链表的长度,则说明是新插入的节点为链表的尾结点 // 如果index大于链表的长度,则返回空 // 如果index小于0,则置为0,作为链表的新头节点。 void addAtIndex(int index, int val) { if (index > _size || index < 0) { return; } LinkedNode* newNode = new LinkedNode(val); LinkedNode* cur = _dummyHead; while(index--) { cur = cur->next; } newNode->next = cur->next; cur->next = newNode; _size++; } // 删除第index个节点,如果index 大于等于链表的长度,直接return,注意index是从0开始的 void deleteAtIndex(int index) { if (index >= _size || index < 0) { return; } LinkedNode* cur = _dummyHead; while(index--) { cur = cur ->next; } LinkedNode* tmp = cur->next; cur->next = cur->next->next; delete tmp; _size--; } // 打印链表 void printLinkedList() { LinkedNode* cur = _dummyHead; while (cur->next != nullptr) { cout << cur->next->val << " "; cur = cur->next; } cout << endl; } private: int _size; LinkedNode* _dummyHead; };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
- 61
- 62
- 63
- 64
- 65
- 66
- 67
- 68
- 69
- 70
- 71
- 72
- 73
- 74
- 75
- 76
- 77
- 78
- 79
- 80
- 81
- 82
- 83
- 84
- 85
- 86
- 87
- 88
- 89
- 90
- 91
- 92
- 93
- 94
- 95
- 96
- 97
- 98
- 99
- 100
- 101
- 102
- 103
- 104
- 105
- 106
- 107
- 108
- 109
- 110
题目三:翻转链表元素
举例Leetcode题目 反转链表:题目地址
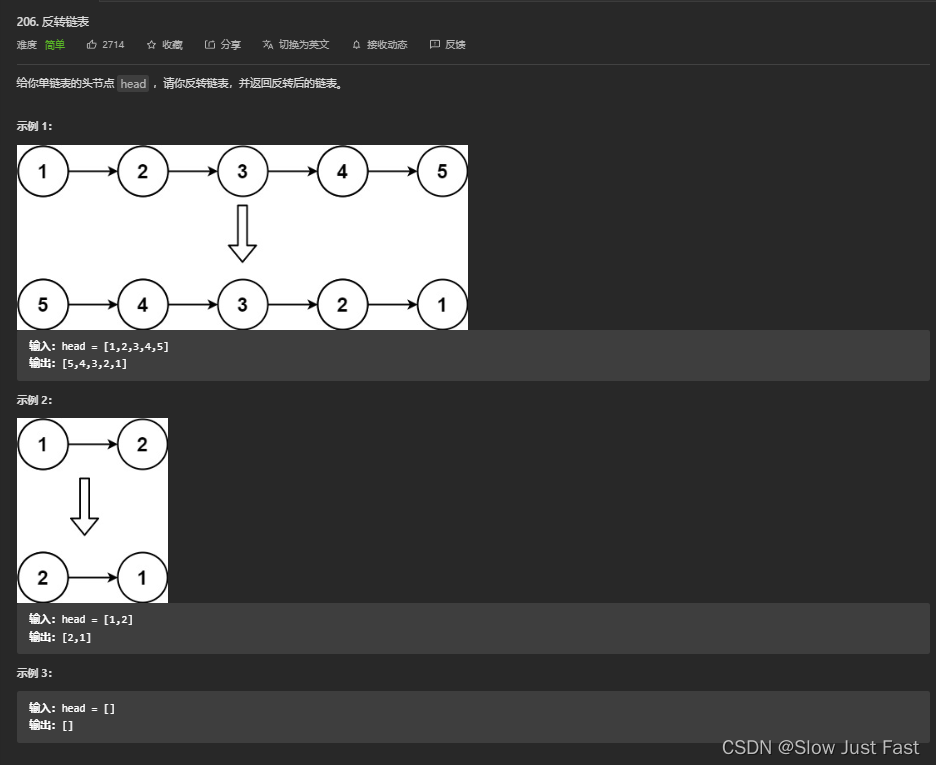
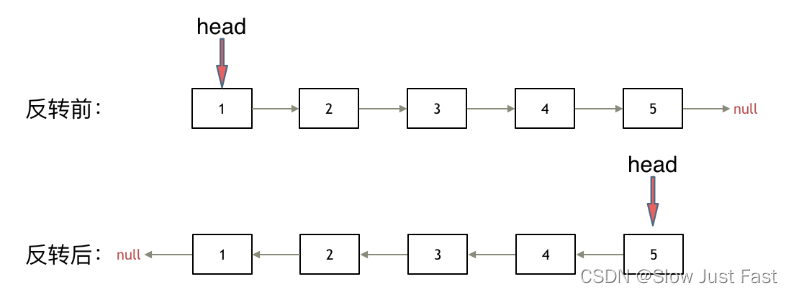
思路一:同向双指针法—通过交换next指针方向实现反向遍历—也可以反向双指针进行元素前后替换
思路二:递归法—通过反复调用原函数实现交换元素
递归法相对抽象一些,但是其实和双指针法是一样的逻辑,同样是当cur为空的时候循环结束,不断将cur指向pre的过程
关键是初始化的地方,可以看到双指针法中初始化 cur = head,pre = NULL,在递归法中可以从如下代码看出初始化的逻辑也是一样的,只不过写法变了
class Solution { public: ListNode* reverseList(ListNode* head) { //双指针法 ListNode* temp; // 保存cur的下一个节点 ListNode* cur = head; ListNode* pre = NULL; while(cur) { temp = cur->next; // 保存一下 cur的下一个节点,因为接下来要改变cur->next cur->next = pre; // 翻转操作 // 更新pre 和 cur指针 pre = cur; cur = temp; } return pre; } }; class Solution { public: ListNode* reverse(ListNode* pre,ListNode* cur) { //递归法 if(cur == NULL) return pre; ListNode* temp = cur->next; cur->next = pre; // 可以和双指针法的代码进行对比,如下递归的写法,其实就是做了这两步 // pre = cur; // cur = temp; return reverse(cur,temp);//新的pre是cur,新的cur是temp,最终返回pre } ListNode* reverseList(ListNode* head) { // 和双指针法初始化是一样的逻辑 // ListNode* cur = head; // ListNode* pre = NULL; return reverse(NULL, head); } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
题目四:范围交换链表元素
举例Leetcode题目 两两交换链表中的结点:题目地址
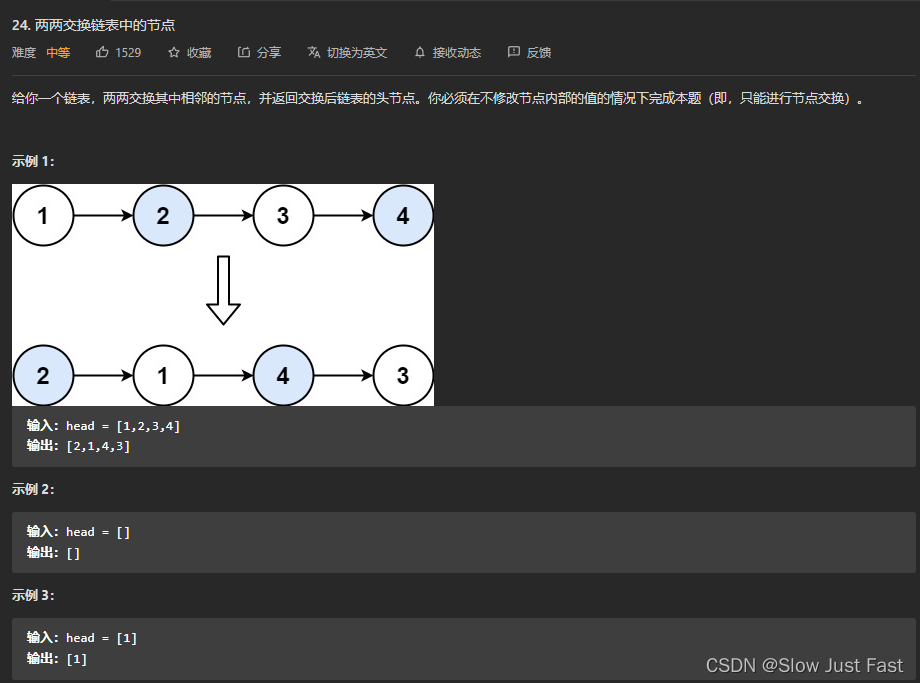
思路:直接用指针去修改位置
class Solution { public: ListNode* swapPairs(ListNode* head) { ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点 dummyHead->next = head; // 将虚拟头结点指向head,这样方面后面做删除操作 ListNode* cur = dummyHead; while(cur->next != nullptr && cur->next->next != nullptr) { ListNode* tmp = cur->next; // 记录临时节点 ListNode* tmp1 = cur->next->next->next; // 记录临时节点 cur->next = cur->next->next; // 步骤一 cur->next->next = tmp; // 步骤二 cur->next->next->next = tmp1; // 步骤三 cur = cur->next->next; // cur移动两位,准备下一轮交换 } return dummyHead->next; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
题目五:指定删除链表元素
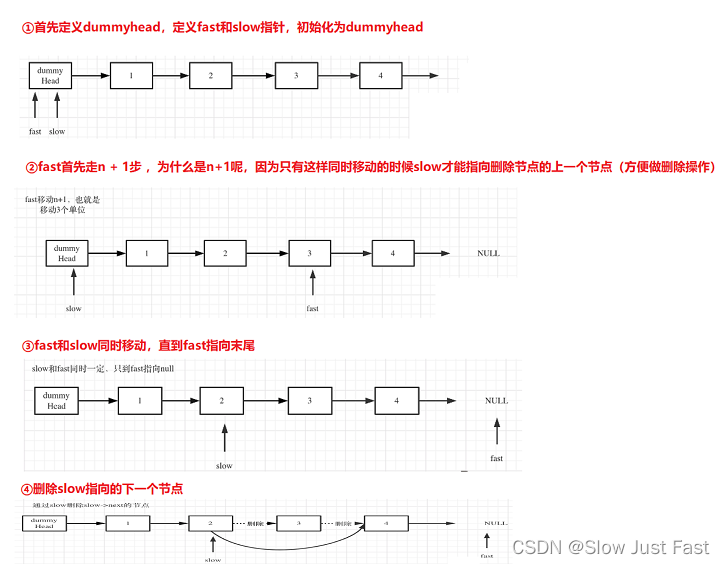
举例Leetcode题目 删除链表的倒数第N个结点:题目地址
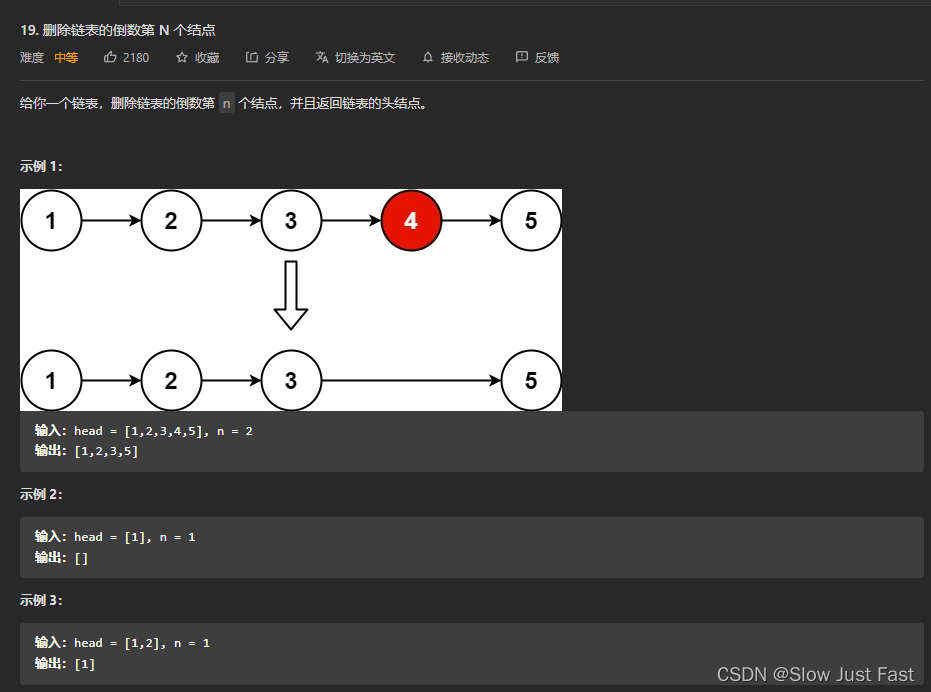
思路:双指针法
class Solution { public: ListNode* removeNthFromEnd(ListNode* head, int n) { ListNode* dummyHead = new ListNode(0); dummyHead->next = head; ListNode* slow = dummyHead; ListNode* fast = dummyHead; while(n-- && fast != NULL) { fast = fast->next; } fast = fast->next; // fast再提前走一步,因为需要让slow指向删除节点的上一个节点 while (fast != NULL) { fast = fast->next; slow = slow->next; } slow->next = slow->next->next; return dummyHead->next; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
题目六:相交链表
举例Leetcode 链表相交:题目地址
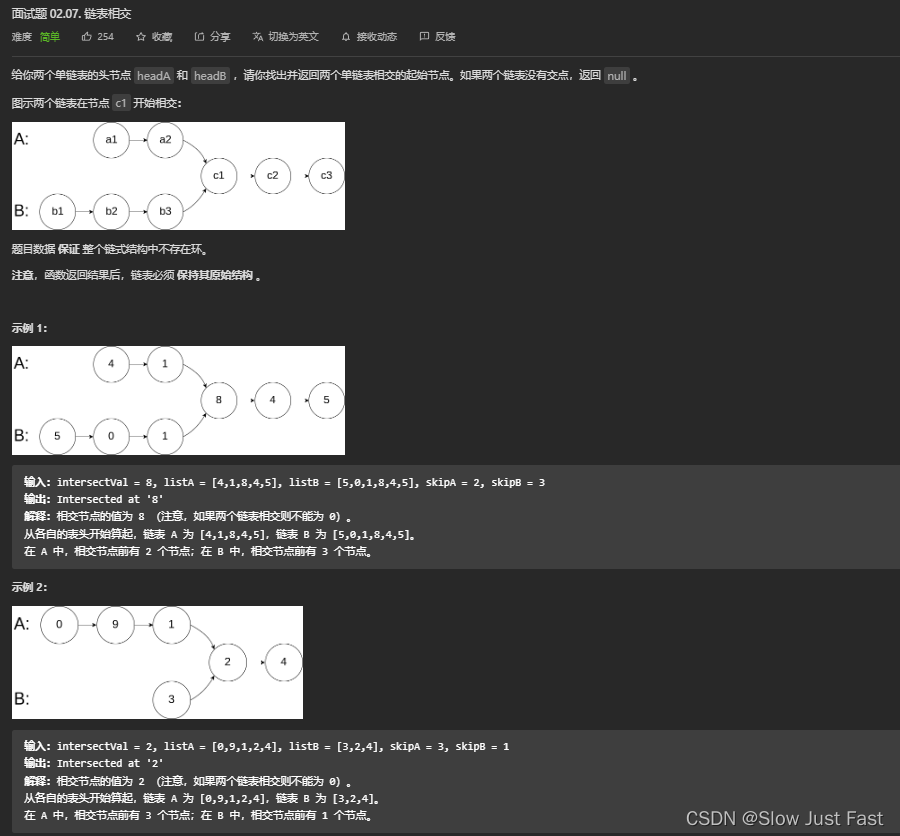
思路:
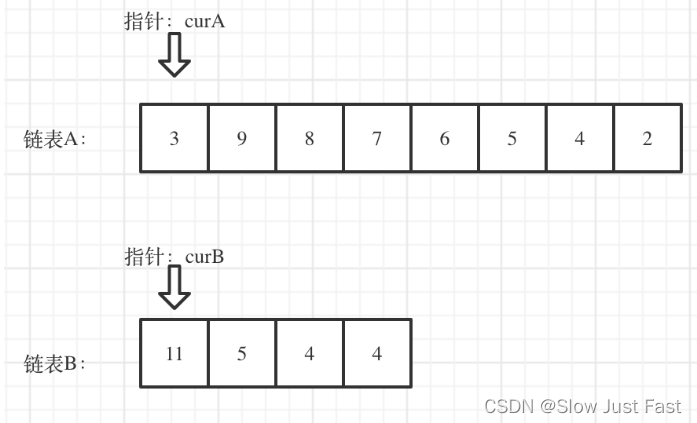
简单来说,就是求两个链表交点节点的指针。 要注意,交点不是数值相等,而是指针相等。
为了方便举例,假设节点元素数值相等,则节点指针相等,有如下两个链表,目前curA指向链表A的头结点,curB指向链表B的头结点:
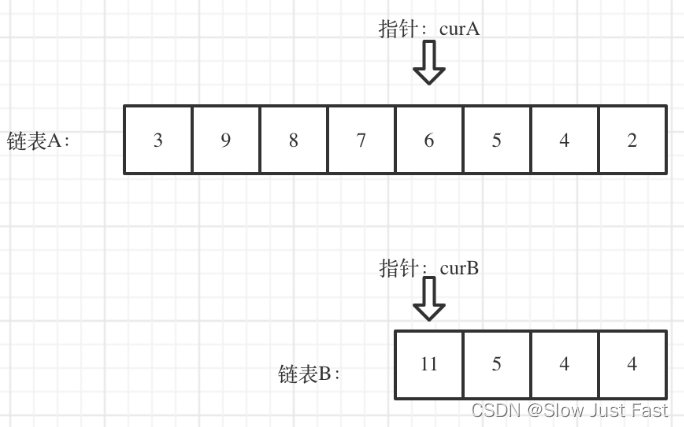
我们求出两个链表的长度,并求出两个链表长度的差值,然后让curA移动到,和curB 末尾对齐的位置,如图:
此时我们就可以比较curA和curB是否相同,如果不相同,同时向后移动curA和curB,如果遇到curA == curB,则找到交点,否则循环退出返回空指针
class Solution { public: ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) { ListNode* curA = headA; ListNode* curB = headB; int lenA = 0, lenB = 0; while (curA != NULL) { // 求链表A的长度 lenA++; curA = curA->next; } while (curB != NULL) { // 求链表B的长度 lenB++; curB = curB->next; } curA = headA; curB = headB; // 让curA为最长链表的头,lenA为其长度 if (lenB > lenA) { swap (lenA, lenB); swap (curA, curB); } // 求长度差 int gap = lenA - lenB; // 让curA和curB在同一起点上(末尾位置对齐) while (gap--) { curA = curA->next; } // 遍历curA 和 curB,遇到相同则直接返回 while (curA != NULL) { if (curA == curB) { return curA; } curA = curA->next; curB = curB->next; } return NULL; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
题目七:环形链表
举例Leetcode题目 环形链表II:题目地址
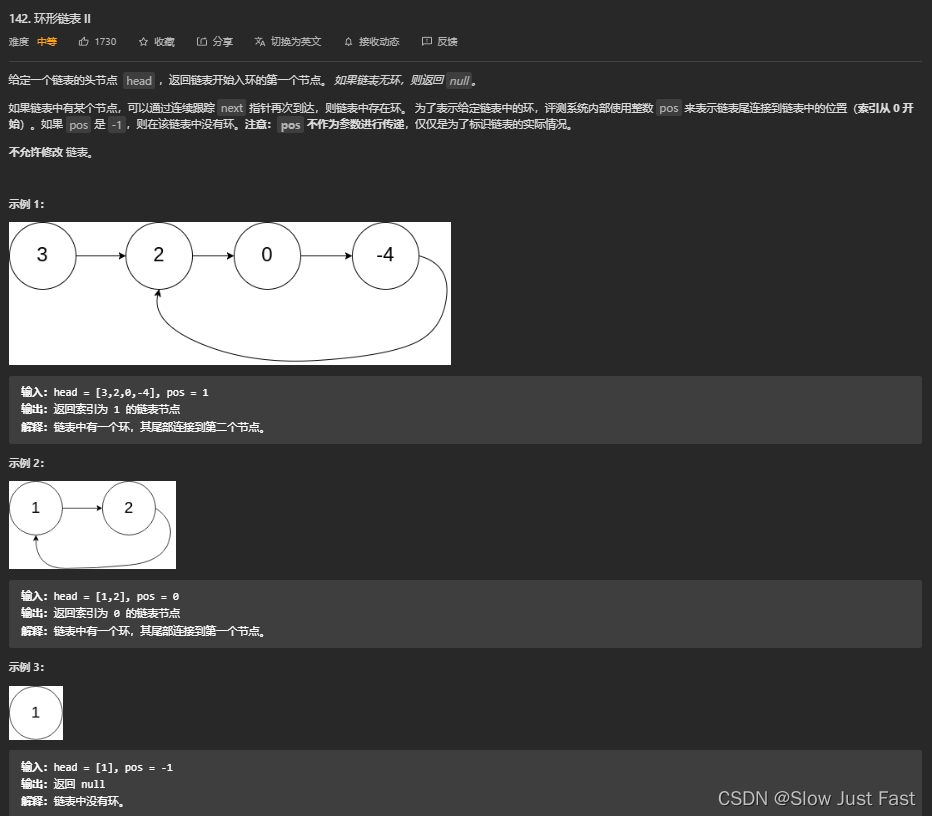
思路:其实主要考察的数学和对于循环链表的基础知识,没有啥思路可言
知识补充:
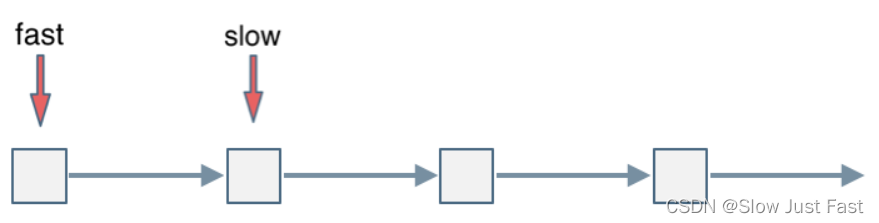
判断链表是否有环方法:可以使用快慢指针法,分别定义 fast 和 slow 指针,从头结点出发,fast指针每次移动两个节点,slow指针每次移动一个节点,如果 fast 和 slow指针在途中相遇 ,说明这个链表有环
为什么fast 走两个节点,slow走一个节点,有环的话,一定会在环内相遇呢,而不是永远的错开呢?
首先第一点:fast指针一定先进入环中,如果fast指针和slow指针相遇的话,一定是在环中相遇,这是毋庸置疑的
那么来看一下,为什么fast指针和slow指针一定会相遇呢?
可以画一个环,然后让 fast指针在任意一个节点开始追赶slow指针,会发现最终都是这种情况, 如下图:
fast和slow各自再走一步, fast和slow就相遇了,不符合要求,所以fast是走两步,slow是走一步,其实相对于slow来说,fast是一个节点一个节点的靠近slow的,所以fast一定可以和slow重合,在环内重合
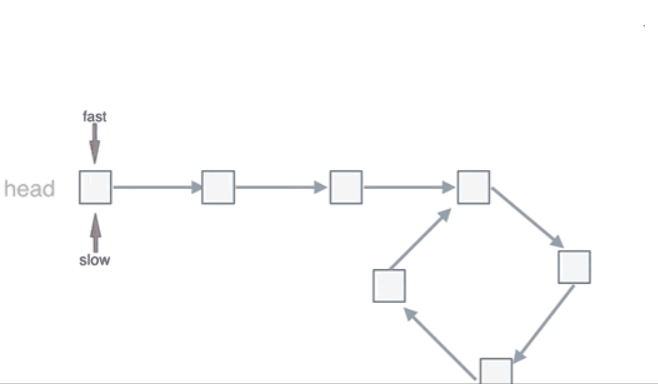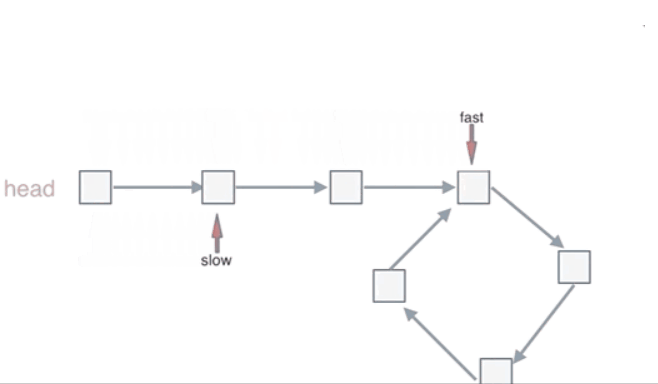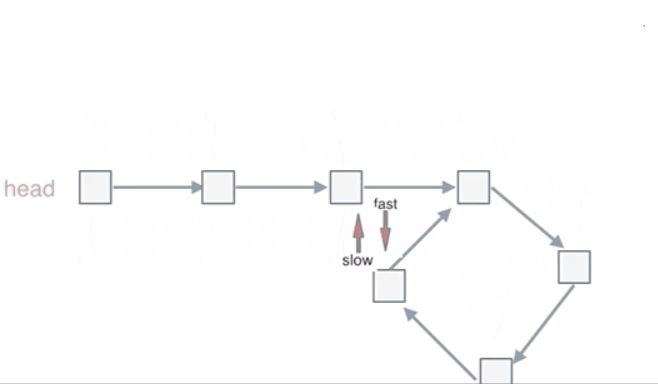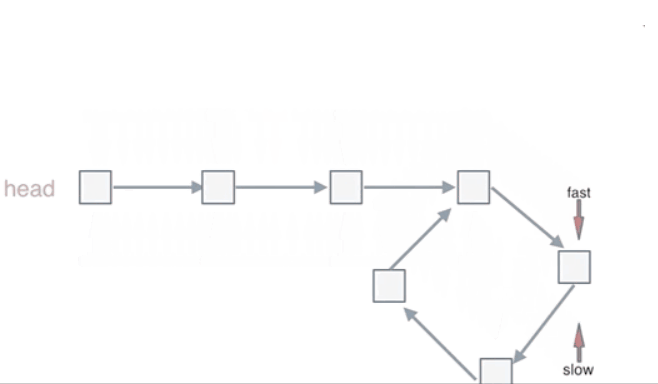
如果有环,如何找到环的入口?
此时已经可以判断链表是否有环了,那么接下来要找这个环的入口了
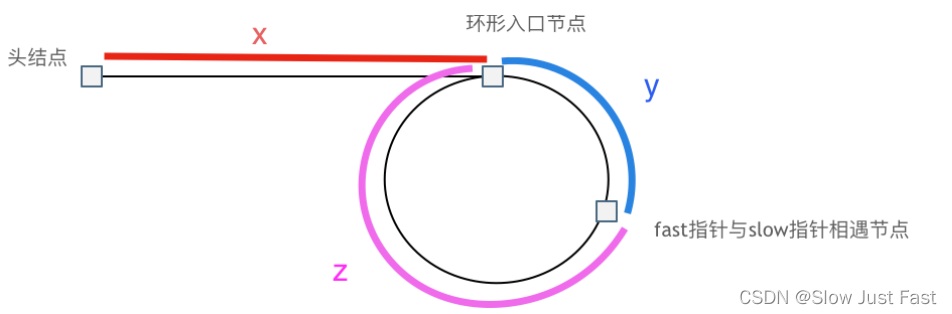
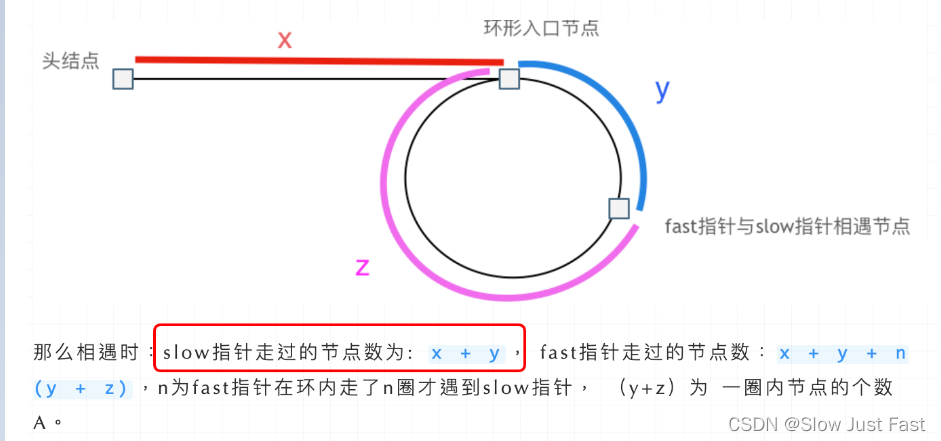
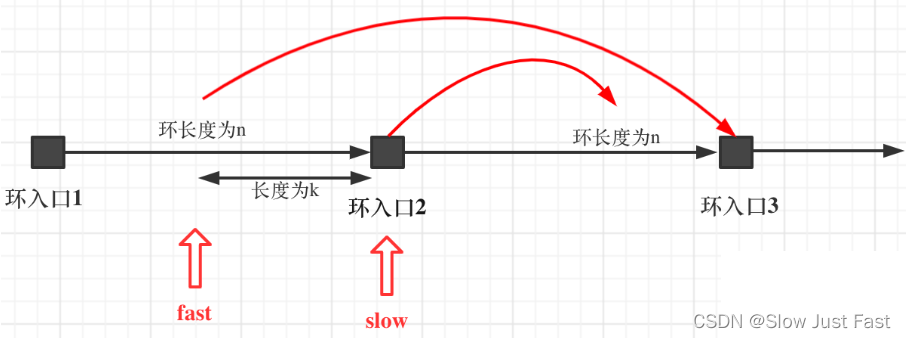
假设从头结点到环形入口节点 的节点数为x。 环形入口节点到 fast指针与slow指针相遇节点节点数为y。 从相遇节点再到环形入口节点节点数为 z。 如图所示:
那么相遇时: slow指针走过的节点数为:
x + y, fast指针走过的节点数:x + y + n (y + z),n为fast指针在环内走了n圈才遇到slow指针, (y+z)为 一圈内节点的个数A。因为fast指针是一步走两个节点,slow指针一步走一个节点, 所以 fast指针走过的节点数 = slow指针走过的节点数 * 2,则有(x + y) * 2 = x + y + n (y + z)
两边消掉一个(x+y):
x + y = n (y + z),因为要找环形的入口,那么要求的是x,因为x表示头结点到环形入口节点的的距离,所以有x = n (y + z) - y,再从n(y+z)中提出一个 (y+z)来,所以有:x = (n - 1) (y + z) + z这个公式说明什么呢?—先拿n为1的情况来举例,意味着fast指针在环形里转了一圈之后,就遇到了 slow指针了,这就意味着,从头结点出发一个指针,从相遇节点也出发一个指针,这两个指针每次只走一个节点, 那么当这两个指针相遇的时候就是环形入口的节点
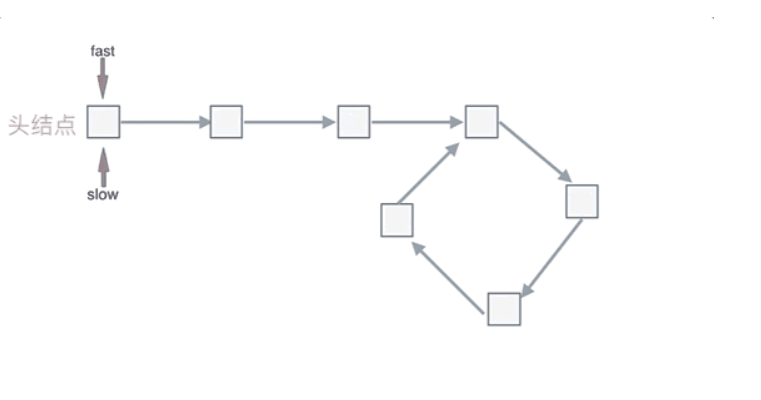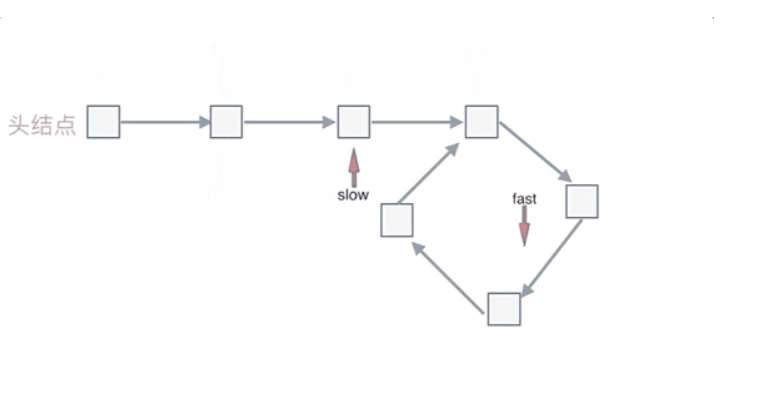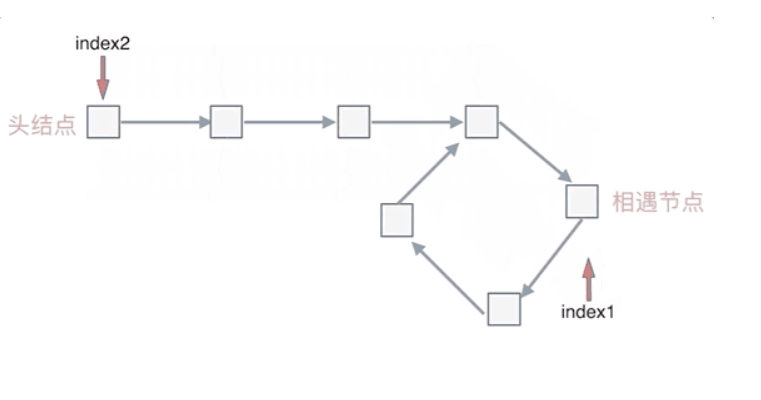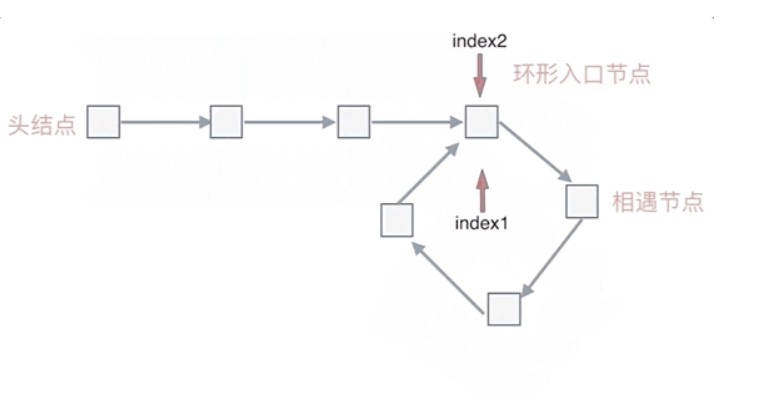
也就是在相遇节点处,定义一个指针index1,在头结点处定一个指针index2,让index1和index2同时移动,每次移动一个节点, 那么他们相遇的地方就是 环形入口的节点
在推理过程中,大家可能有一个疑问就是:为什么第一次在环中相遇,slow的 步数 是 x+y 而不是 x + 若干环的长度 + y 呢?
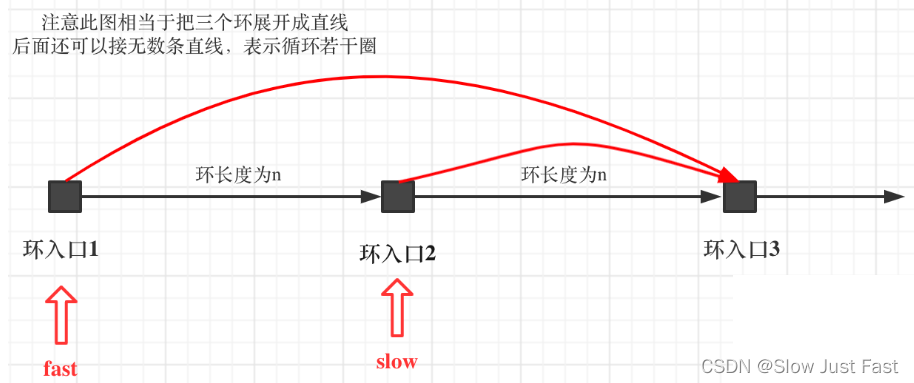
首先slow进环的时候,fast一定是先进环来了,如果slow进环入口,fast也在环入口,那么把这个环展开成直线,就是如下图的样子:
可以看出如果slow和fast同时在环入口开始走,一定会在环入口3相遇,slow走了一圈,fast走了两圈。slow进环的时候,fast一定是在环的任意一个位置,如图:
那么fast指针走到环入口3的时候,已经走了k + n 个节点,slow相应的应该走了(k + n) / 2 个节点。因为k是小于n的(图中可以看出),所以(k + n) / 2 一定小于n。也就是说slow一定没有走到环入口3,而fast已经到环入口3了。
这说明什么呢?—在slow开始走的那一环已经和fast相遇了
为什么fast不能跳过去呢?—因为fast相对于slow是一次移动一个节点,所以不可能跳过去
class Solution { public: ListNode *detectCycle(ListNode *head) { ListNode* fast = head; ListNode* slow = head; while(fast != NULL && fast->next != NULL) { slow = slow->next; fast = fast->next->next; // 快慢指针相遇,此时从head 和 相遇点,同时查找直至相遇 if (slow == fast) { ListNode* index1 = fast; ListNode* index2 = head; while (index1 != index2) { index1 = index1->next; index2 = index2->next; } return index2; // 返回环的入口 } } return NULL; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26