LeetCode-152. 乘积最大子数组【数组 动态规划】

题目描述：

给你一个整数数组 nums ，请你找出数组中乘积最大的非空连续
子数组
（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

测试用例的答案是一个 32-位 整数。

示例 1:

输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:

输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。

提示:

1 <= nums.length <= 2 * 10⁴
-10 <= nums[i] <= 10
nums 的任何前缀或后缀的乘积都 保证 是一个 32-位 整数

解题思路一：动态规划五部曲：定推初遍举

1. dp定义
   以下标 i 结尾的连续子序列的乘积的最大值。
   牢记状态的定义，一定以下标 i 结尾，即：乘积数组中 nums[i] 必须被选取。
   • 如果 dp[i - 1] 是负数，乘上 nums[i] 还是负数，倒不如另起炉灶。
   • 如果 nums[i] 是负数该怎么办呢？dp[i - 1] 是正数的时候，越乘越小，dp[i - 1] 是负数的时候，越乘越大，于是我们可能就需要记录一下负数的那个最小数。

遇到这样的问题，其实就在提示我们状态不够用了。因此，需要在原来的一维 dp 后面新增一个状态。

针对这道题，第 2 维状态只需要两个：

• 用 0 表示遍历的过程中得到的以 nums[i] 结尾的连续子序列的乘积的最小值；
• 用 1 表示遍历的过程中得到的以 nums[i] 结尾的连续子序列的乘积的最大值。

当 nums[i] = 0 的时候包含在上面二者之中，无需单独讨论。

状态转移方程写在了参考代码 1 中。即使用二维状态数组同时记录乘积的最大值和最小值，本来写了一堆文字的，后来看太长了，好多废话，直接看代码比较清楚一些。

这里就声明一下状态：

dp[i][1] 表示：以 nums[i] 结尾的连续子序列的乘积的最大值；
dp[i][0] 表示：以 nums[i] 结尾的连续子序列的乘积的最小值。

2. 推导公式

if nums[i] >= 0:
                dp[i][1] = max(nums[i], dp[i-1][1] * nums[i])
                dp[i][0] = min(nums[i], dp[i-1][0] * nums[i])
            else:
                dp[i][1] = max(nums[i], dp[i-1][0] * nums[i])
                dp[i][0] = max(nums[i], dp[i-1][1] * nums[i])
1
2
3
4
5
6

3. 初始化

dp = [[0, 0] for _ in range(n)]
        dp[0][0] = nums[0]
        dp[0][1] = nums[0]
1
2
3

4. 遍历顺序，显然是从前往后

for i in range(1, n):
1

5. 举例
   

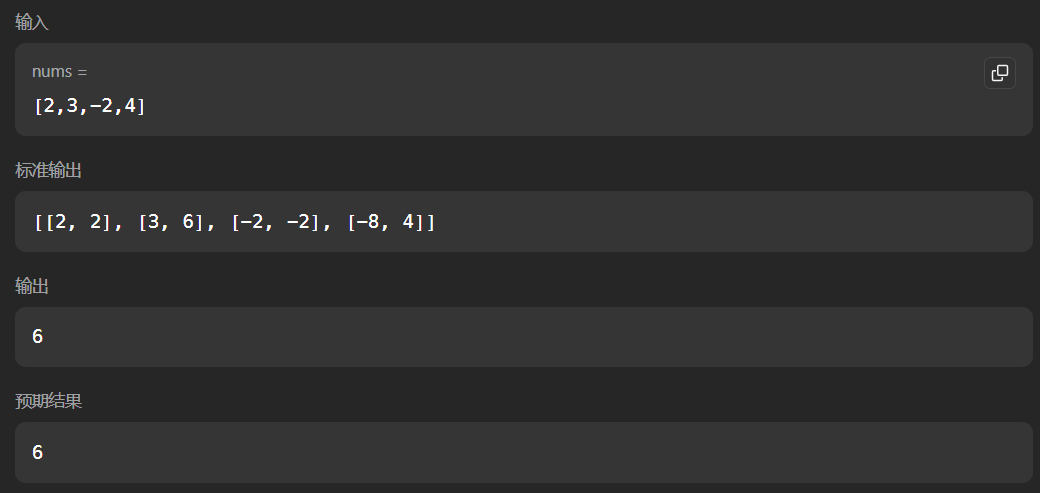
class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        n = len(nums)
        if n == 0:
            return 0
        dp = [[0, 0] for _ in range(n)]
        dp[0][0] = nums[0]
        dp[0][1] = nums[0]
        for i in range(1, n):
            if nums[i] >= 0:
                dp[i][1] = max(nums[i], dp[i-1][1] * nums[i])
                dp[i][0] = min(nums[i], dp[i-1][0] * nums[i])
            else:
                dp[i][1] = max(nums[i], dp[i-1][0] * nums[i])
                dp[i][0] = min(nums[i], dp[i-1][1] * nums[i])
        # print(dp)
        ans = dp[0][1]
        for i in range(1, n):
            ans = max(ans, dp[i][1])
        return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

时间复杂度：O(n)
空间复杂度：O(n)

解题思路二：因为每一个状态只与前一个状态有关，可以使用「滚动变量」技巧，使用常数个变量完成这道问题。

class Solution:
    def maxProduct(self, nums: List[int]) -> int:
        n = len(nums)
        if n == 0:
            return 0
        # dp = [[0, 0] for _ in range(n)]
        # dp[0][0] = nums[0]
        # dp[0][1] = nums[0]
        preMax = nums[0]
        preMin = nums[0]
        curMax = preMax
        curMin = preMin
        ans = nums[0]
        for i in range(1, n):
            if nums[i] >= 0:
                curMax = max(nums[i], preMax * nums[i])
                curMin = min(nums[i], preMin * nums[i])
            else:
                curMax = max(nums[i], preMin * nums[i])
                curMin = min(nums[i], preMax * nums[i])
            ans = max(ans, curMax)
            # 滚动变量
            preMax = curMax
            preMin = curMin
        return ans
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

时间复杂度：O(n)
空间复杂度：O(1)

解题思路三：0

1

时间复杂度：O(n)
空间复杂度：O(n)