力扣：63. 不同路径 II（动态规划）_力扣网路径

题目：

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

示例 1：

输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出：2
解释：3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径：

1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右

示例 2：

输入：obstacleGrid = [[0,1],[0,0]]
输出：1

提示：

m == obstacleGrid.length
n == obstacleGrid[i].length
1 <= m, n <= 100
obstacleGrid[i][j] 为 0 或 1

思路：

这道题相对于力扣：62. 不同路径（动态规划，附python二维数组的定义）就是有了障碍。
不同路径中我们已经详细分析了没有障碍的情况，有障碍的话，其实就是标记对应的dp数组保持初始值0就可以了。

动规五部曲：

1. 确定dp数组以及下标的含义（跟上题一样）

这里要明确dp数组的含义，定义dp数组是为了找到不同路径，
dp[i][j] ：表示从（0 ，0）出发，到(i, j) 有dp[i][j]条不同的路径。

2. 确定递推公式

递归公式跟上题一样，dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。
但这里需要注意一点，因为有了障碍，(i, j)如果就是障碍的话应该就保持初始状态（初始状态为0）。

代码如下：

                if obstacleGrid[i][j] == 0:
                    dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
1
2

3. dp数组如何初始化

这里的初始化是重点，
如果(i, 0) 这条边有了障碍之后，障碍之后（包括障碍）都是走不到的位置了，所以障碍之后的dp[i][0]应该还是初始值0。下标(0, j)的初始化情况同理。

所以本题初始化代码为：

        for i in range(n):
            if obstacleGrid[0][i] == 0:
                dp[0][i] = 1
            else:
                break
        for j in range(m):
            if obstacleGrid[j][0] == 0:
                dp[j][0] = 1
            else:
                break
1
2
3
4
5
6
7
8
9
10

注意：一旦遇到obstacleGrid[i][0] == 1的情况，一定要退出循环！不然之后障碍之后的点依旧会被赋值。

4. 确定遍历顺序（跟上题一样）

从递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1] 中可以看出，一定是从左到右一层一层遍历，这样保证推导dp[i][j]的时候，dp[i - 1][j] 和 dp[i][j - 1]一定是有数值。

5. 举例推导dp数组

拿示例1来举例如题：

对应的dp数组如图：

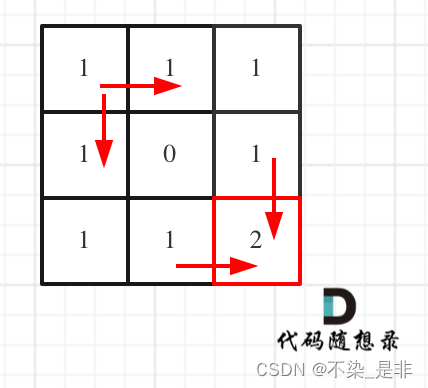
完整代码：

class Solution:
    def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
        # 获取网格的列数和行数
        n = len(obstacleGrid[0])
        m = len(obstacleGrid)
        
        # 如果起点或终点有障碍物，直接返回0
        if obstacleGrid[0][0] == 1 or obstacleGrid[m - 1][n - 1] == 1:
            return 0
        
        # 初始化一个二维数组dp，用于存储到达每个位置的路径数量
        dp = [[0] * n for _ in range(m)]
        
        # 初始化第一行，如果没有障碍物，则到达每个位置的路径数量为1，否则后面的位置均不可达
        for i in range(n):
            if obstacleGrid[0][i] == 0:
                dp[0][i] = 1
            else:
                break
        
        # 初始化第一列，如果没有障碍物，则到达每个位置的路径数量为1，否则后面的位置均不可达
        for j in range(m):
            if obstacleGrid[j][0] == 0:
                dp[j][0] = 1
            else:
                break
        
        # 计算其余位置的路径数量
        for i in range(1, m):
            for j in range(1, n):
                # 如果当前位置没有障碍物，则到达当前位置的路径数量为到达上方和左方位置的路径数量之和
                if obstacleGrid[i][j] == 0:
                    dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
        
        # 返回到达终点的路径数量
        return dp[m - 1][n - 1]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

复杂度分析：

• 时间复杂度：O(n × m)，n、m 分别为obstacleGrid 长度和宽度
• 空间复杂度：O(n × m)