【算法】图的最小生成树(Kruskal算法)_kruskal算法求最小生成树

这篇文章是2.0版本，修正了前一版中的错误，感谢广大网友指正！ 

前面介绍了图的最小生成树的Prim算法，这个算法是从顶点的角度来刻画生成树的。今天要说的Kruskal(克鲁斯卡尔)算法，是从边的角度来进行刻画的。

  Kruskal算法用到的数据结构有：

  1、边顶点与权值存储结构(即图是由连接某一条边的两个顶点，以及这条边的权值来进行存储，具体看后面的例子)

  2、并查集(具体是什么以及作用在后面的例子中解释)

  Kruskal算法步骤 -- 我们今天要实现的目标依然与前面Prim算法的相同，计算最小生成树的权值之和

  1、前期准备(数据结构)

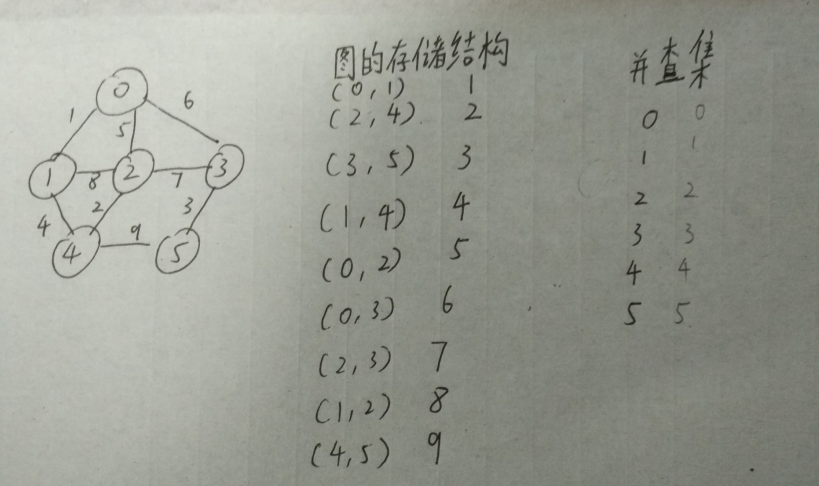
在无向图右边的便是图的存储结构，可以看出这个存储结构不同于我们所熟知的邻接矩阵和邻接表，这个存储结构的每一项，以边为单位，存储着连接这条边的两个顶点，以及这条边的权值。比如第一项，顶点0与顶点1邻接，这条边的权值为1，所以左边填入(0,1)，右边为1。这个顶点谁先谁后都可以。存储结构以边为基准，有几条边就有几项。

在存储结构的右边就是上面提到的并查集了，并查集就是一个用双亲表示法所表示的森林，我们可以利用这个结构来查找某一个顶点的双亲，进而找到根结点。这样，我们就能判断某两个顶点是否同源，在图中的表现就是加上这条边后会不会形成环。如果形成环，就不是简单图，就不属于考研(好吧，LL在准备考研，怕忘了，就记录下来)数据结构的研究范围了。并查集以顶点为基准，有几个顶点，就有几项。

PS.这里适用与顶点编号连续的情况，这样在并查集中，数组的下标就对应顶点的编号，数组的值就是这个顶点所在的双亲。这就是树的双亲表示法。高效率地利用数组下标。

2、算法步骤

     a、对图的存储结构，按照权值，从小到大排序。（上图是已经排序好的）

     b、对并查集进行初始化，即把每一个位置中的值初始化为其对应下标。(上图是已经初始化好的)

     c、选取存储结构的第一项(最小项)，查询该边所对应的顶点在并查集中是否同源，同源则进行e，不同源则进行d

     d、若不同源，则把该边加入生成树，并计算和；修改前者的根在并查集中位置的值为后者的根。如下图：第一项(0,1)不同源，顶点0的根为0，顶点1的根为1，设a为并查集数组，把a[0] = 1，即把并查集中下标为0的位置中的值修改为1。这样，(0,1)这条路径就加入了最小生成树。

 

        e、若同源，则跳过，继续遍历存储结构，如下图

Now指针指的是现在所处理的项，顶点0的根为4(因为第0个结点的双亲是结点1，结点1的双亲是结点4，结点4的双亲是它自己，说明结点4就是结点0的根结点)，顶点2的根也为4，则跳过该项，继续遍历。

       f、重复d~e，直到存储结构中所有的项被遍历。

现在就到代码阶段了。

我们要准备以下函数：

1、排序函数sort，任何一种排序算法都行，下面的示例代码中，我采用的是冒泡排序算法

2、寻源函数getRoot，寻找某一个点在并查集中的根，注意，是根，不是双亲！，所以，判断的条件为如果某一个下标的值就是其本身，设a为并查集数组，v为数组值，如果a[v] = v，它就是根，否则就让v = a[v]，向上寻找，直到其相等。

下面上代码

1、图的存储结构(a，b为边的两个顶点，w为边的权值)

 

#define Max 50
typedef struct road *Road;
typedef struct road
{
	int a , b;
	int w;
}road;
typedef struct graph *Graph;
typedef struct graph
{
	int e , n;
	Road data;
}graph;

2、排序sort函数（按照权值从小到大）

 

 

void sort(Road data, int n)
{
	int i , j;
	for(i = 1 ; i <= n-1 ; i++)
	{
		for(j = 1 ; j <= n-i ; j++)
		{
			if(data[j].w > data[j+1].w)
			{
				road t = data[j];
				data[j] = data[j+1];
				data[j+1] = t;
			}
		}
	}
}

3、getRoot寻源函数（v为并查集，x为待查顶点）

 

 

int getRoot(int v[], int x)
{
	while(v[x] != x)
	{
		x = v[x];
	}
	return x;
}

4、完整代码（我这里顶点采用了先小后大的排序）

 

 

#include <stdio.h>
#include <stdlib.h>
#define Max 50
typedef struct road *Road;
typedef struct road
{
	int a , b;
	int w;
}road;
 
typedef struct graph *Graph;
typedef struct graph
{
	int e , n;
	Road data;
}graph;
 
Graph initGraph(int m , int n)
{
	Graph g = (Graph)malloc(sizeof(graph));
	g->n = m;
	g->e = n;
	g->data = (Road)malloc(sizeof(road) * (g->e));
	return g;
}
 
void create(Graph g)
{
	int i;
	for(i = 1 ; i <= g->e ; i++)
	{
		int x , y, w;
		scanf("%d %d %d",&x,&y,&w);
		if(x < y)
		{
			g->data[i].a = x;
			g->data[i].b = y;
		}
		else
		{
			g->data[i].a = y;
			g->data[i].b = x;
		}
		g->data[i].w = w;
	}
}
 
int getRoot(int v[], int x)
{
	while(v[x] != x)
	{
		x = v[x];
	}
	return x;
}
 
void sort(Road data, int n)
{
	int i , j;
	for(i = 1 ; i <= n-1 ; i++)
	{
		for(j = 1 ; j <= n-i ; j++)
		{
			if(data[j].w > data[j+1].w)
			{
				road t = data[j];
				data[j] = data[j+1];
				data[j+1] = t;
			}
		}
	}
}
 
int Kruskal(Graph g)
{
	int sum = 0;
	//并查集
	int v[Max];
	int i;
	//init
	for(i = 1 ; i <= g->n ; i++)
	{
		v[i] = i;
	}
	sort(g->data , g->e);
	//main
	for(i = 1 ; i <= g->e ; i++)
	{
		int a , b;
		a = getRoot(v,g->data[i].a);
		b = getRoot(v,g->data[i].b);
		if(a != b)
		{
			v[a] = b;
			sum += g->data[i].w;
		}
	}
	return sum;
}
 
int main()
{
	int m , n , id = 1;
	while(scanf("%d %d",&m,&n) != EOF)
	{
		int r , i;
		Graph g = initGraph(m,n);
		create(g);
		r = Kruskal(g);
		printf("Case %d:%d\n",id++,r);
		free(g);
	}
	return 0;
}

输入数据：

第一行两个整数表示图的顶点和边的个数

然后接下来的若干行，第一个数表示起点，第二个数表示终点，第三个数表示权值

6 10
1 2 16
1 6 21
1 5 19
2 3 5
2 4 6
2 6 11
3 4 6
6 4 14
5 4 18
5 6 33
2 1
1 2 9

运行结果：