自己动手写chatGPT:神经网络的神经元和损失函数_gpt损失函数

chatGPT基于所谓的大模型，这里有两个关键词一个是“大”，一个是“模型”，我们先看什么叫“模型”。所谓模型其实就是深度学习中的神经网络，后者由很多个称之为“神经元”基本单元组成。神经元是一种基础计算单元，它执行两种操作，首先是一个矩阵M和输入向量X做乘法操作，其结果是一维向量WX，然后再跟另一个一维向量b做加法操作，所得结果还是一维向量WX + b,这些步骤统称为线性运算，最后这个一维向量会输入到一个函数f，最终输出结果是也是一个向量f(W*X + b)，这个步骤叫非线性操作，其基本流程如下：

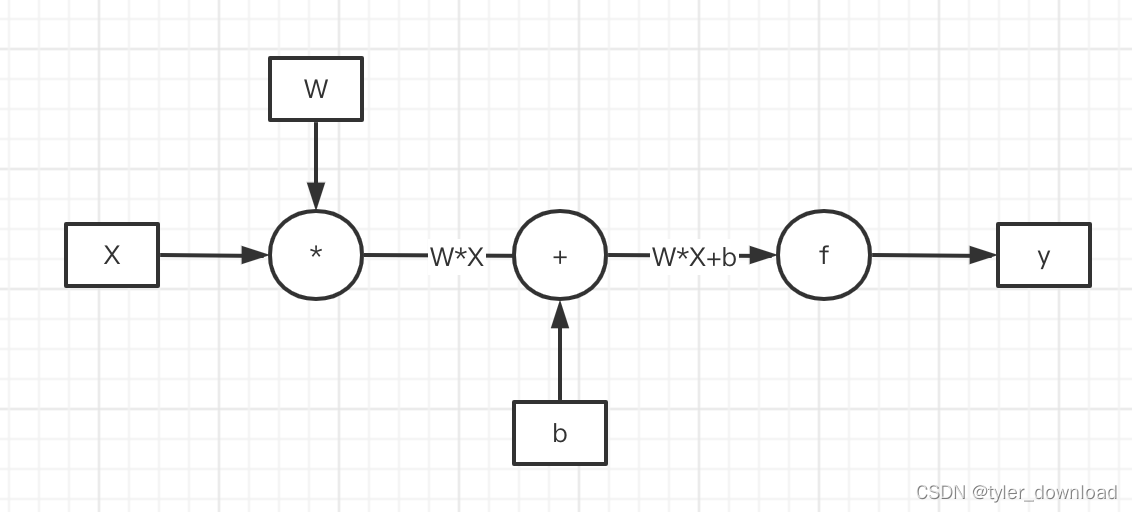
chatGPT的参数有1750亿个，也就是说它由1750亿个像上面那样的计算单元相互连接所形成的超大网络组成。上面流程中有一个关键步骤那就是函数f的执行，它也叫激活函数，其目的是把把前面线性运算的结果做某种非线性的跃迁，它主要有四种类型，第一种叫sigmoid,它的表达式为1 / (1 + e^(-x))，我们看看其函数图形：

import torch
import matplotlib.pyplot as plt

#创建x插值点[-5.0, -4.9, -4.8,...., 5.0]
x = torch.range(-5., 5., 0.1)
print(f"x:{x}")
#执行激活函数
y = torch.sigmoid(x)
print(f"y:{y}")
#根据插值绘图
plt.plot(x.numpy(), y.numpy())
1
2
3
4
5
6
7
8
9
10
11

上面代码执行后输出图形如下：

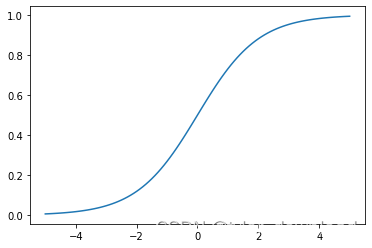
它的输出结果在0到1之间，如果我们想让网络预测某种概率，那么我们就可以在网络的末尾使用这个函数，它存在一个问题，那就是在x接近1.0或0的地方，如果对这些位置的x求导的话，切线的斜率就会非常接近0，这在训练网络时会产生一种叫"vanishing gradient"的问题。

第二种激活函数叫tanh(x), 它的表达式为(e^(x)- e ^ (-x)) / (e ^ (x) + e ^ (-x)),我们用下面代码画出其函数图形：

import torch 
import matplotlib.pyplot as plt
x = torch.range(-5., 5., 0.1)
y = torch.tanh(x) 
plt.plot(x.numpy(), y.numpy()) 
plt.show()
1
2
3
4
5
6

上面代码运行后结果如下：

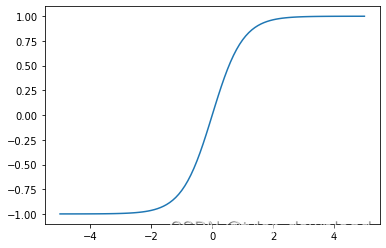
第三种叫ReLU，它是最重要也是应用最多的一种激活函数，它的解析式为f(x)= max(0,x)，它看起来简单，但在实用中却相当有效，我们看看它的图形：

import torch
import matplotlib.pyplot as plt

relu = torch.nn.ReLU()
x = torch.range(-5., 5., 0.1)
y = relu(x)

plt.plot(x.numpy(), y.numpy())
plt.show()
1
2
3
4
5
6
7
8
9

上面代码运行后结果如下：

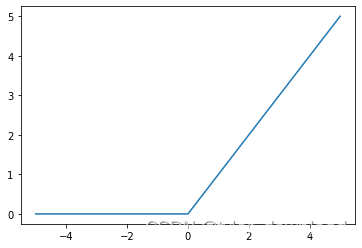
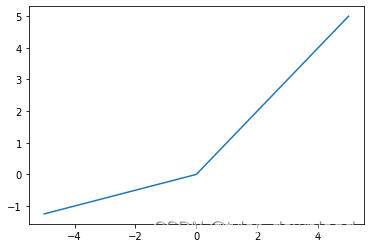
它的逻辑很简单，就是把所有小于0的值转换为0，大于0的保持不变。它有个问题就是在小于0的区域，它的图像是一条直线，这意味着在这个区域对其求导所得结果都是0，这对网络的训练会带来不利影响，因此它有一个变体叫leaky ReLU, 函数为f(x)=max(x, ax)，其中参数a需要通过网络的训练来得出，我们看看其函数图形：

import torch 
import matplotlib.pyplot as plt
prelu = torch.nn.PReLU(num_parameters=1) 
x = torch.range(-5., 5., 0.1)
y = prelu(x)
plt.plot(x.numpy(), y.detach().numpy()) 
plt.show()
1
2
3
4
5
6
7

最后一个常用的激活函数叫softmax，它的作用是在给定的若干个选项中计算每个选项的百分比，例如我们判断一张图片里的动物是猫还是狗，那么这个函数就会给出两个结果分别对应是还是狗的概率。这个函数的表达式为： softmax(xi) = (e ^xi) / ( e ^ x1 + e ^ x2 + … + e ^xk),我们看看该函数的相关代码：

import torch.nn as nn 
import torch 

softmax = nn.Softmax(dim = 1)
x_input = torch.randn(1,3)
#y_output对应向量中所有分量加总为1
y_output = softmax(x_input)
describeTensor(x_input)
describeTensor(y_output)
#把输出结果的分量加总
print(torch.sum(y_output, dim=1))
1
2
3
4
5
6
7
8
9
10
11

上面代码执行后结果如下：

Type: torch.FloatTensor
shape/size: torch.Size([1, 3])
values: tensor([[ 0.7110,  0.0178, -0.8281]])
Type: torch.FloatTensor
shape/size: torch.Size([1, 3])
values: tensor([[0.5832, 0.2916, 0.1251]])
tensor([1.])
1
2
3
4
5
6
7

在深度学习中还有一个重要概念就是损失函数。它其实是一种数学的方式来描述结果的好坏。假设我们有一个网络用来识别输入图片是猫还是狗，网络输出两个数值，一个数值对应是狗的概率，另一个数值对应是猫的概率。如果网络识别能力足够强，那么输入一张狗的图片时，对应狗的概率数值要尽可能大，对应猫的数值要尽可能小，损失函数就是要用数学函数的方式来描述“对应狗的概率数值要尽可能大，对应猫的数值要尽可能小”这种情况。

在“有监督学习”的情况下，网络在训练时输入数据会有对应的答案，例如我们训练网络识别猫狗图片时，每张图片还会对应有一个标记值，如果是狗图片，那么标记1.0，如果是猫图片，那么标记0，我们用y来表示这个标记值，用y^表示网络给出图片是猫还是狗的概率，我们可以用多种公式来描述网络输出的准确度，第一种叫平方和平均(MSE)，其公式如下：

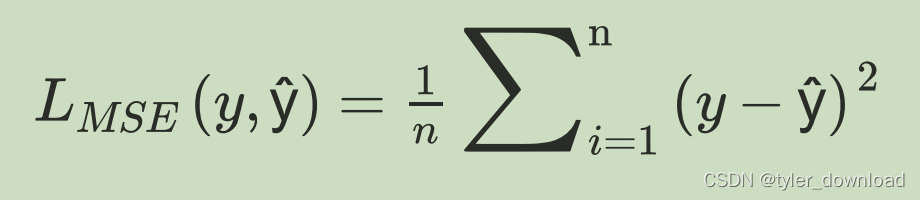
pytorch框架提供了这个函数，我们可以直接调用，代码如下：

import torch
import torch.nn as nn 
mse_loss = nn.MSELoss()
outputs = torch.Tensor([1,2])
targets = torch.Tensor([3,4])
#[(3-1)^2 + (4-2)^2] / 2
loss = mse_loss(outputs, targets)
print(loss)
1
2
3
4
5
6
7
8

上面代码输出结果为4.0，

第二种损失函数叫交叉熵，其公式为：

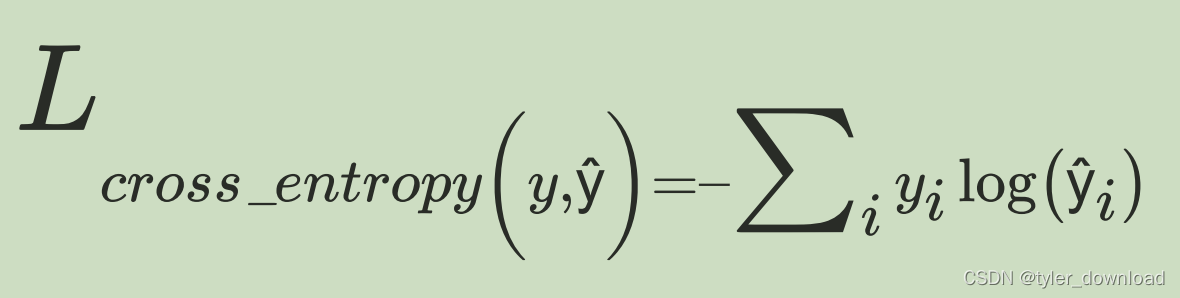
这个公式常用于判断输入属于哪种类别，它的使用要基于前面描述的softmax函数。假设网络要判断的输入图片中物品的种类有四种，分别为猫，狗，牛，羊，我们用one-hot-vector来表示这五种不同类型，如果是猫，对应向量就是[1,0,0,],如果是狗，那么就是[0,1,0,0,]，以此类推。

当我们把一张猫图片输入网络，网络使用softmax计算五种物体的可能性，例如输出为[0.775, 0.116, 0.039,0.070]，那么对应到上面公式，i的取值就是0到4，y0=1,y1=0,y2=0,y3=0, y ^ 0 = 0.775, y ^ 1 = 0.116, y ^ 2 = 0.039, y ^ 4 = 0.070，当我们调整网络内部参数，让它输出的结果代入上面公式后所得结果尽可能小，这种调节的结果就使得网络在接收猫图片后，它输出的第0个分量对应的数值要尽可能的大。

我们看看如何使用pytorch调用上面的损失函数:

import torch
import torch.nn as nn

ce_loss = nn.CrossEntropyLoss()

outputs = torch.randn(3,5)
print(outputs)
'''
outputs对应向量会在CrossEntropyLoss中进行softmax运算，将其分量正规化
1对应向量[0, 1, 0, 0, 0]
0对应向量[1, 0, 0, 0, 0]
4对应向量[0, 0, 0, 0, 1]
分别用上面向量跟outputs中对应向量进行cross entropy 计算，最终把三个计算结果加总求平均后输出
'''
targets = torch.tensor([1, 0, 4], dtype = torch.int64)
loss = ce_loss(outputs, targets)
print(loss)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

上面代码运行后输出一个数值，由于outputs是随机初始化的向量，因此每次运行输出结果都有不同。

最后还有一种损失函数是上面的变种叫二进制交叉熵损失，它主要把类别现在在两种以内，因此targets中的元素值不超过1 ，同时outputs中元素的值要在0和1之间，我们看看代码：

bce_loss = nn.BCELoss()
sigmoid = nn.Sigmoid()
probabilities = sigmoid(torch.randn(4,1)) #把分量取值在0,1之间
#view(4,1)把一个包含4个分量的一维向量转换成一个包含4个一维向量的2维数组，每个向量只包含一个元素
targets = torch.tensor([1, 0, 1, 0], dtype=torch.float32).view(4,1)
loss = bce_loss(probabilities, targets)
print(probabilities)
print(loss)
1
2
3
4
5
6
7
8

上面代码运行后输出为：

tensor([[0.6935],
        [0.8990],
        [0.6251],
        [0.3131]])
tensor(0.8760)
1
2
3
4
5

更多内容请在b站搜索Coding迪斯尼。