- 1《SteamVR2.2.0快速入门》(Yanlz+Unity+XR+OpenVR+OpenXR+SteamVR+Valve+Vive+Oculus+Quickstart+HMD+立钻哥哥++ok++)_steamvr openvr区别
- 2爱奇艺DRM修炼之路
- 3python小游戏毕设 炸弹人小游戏设计与实现 (源码)
- 4(附源码)Springboot数字化超市管理系统设计与实现 计算机毕设34804_基于springboot的超市管理系统的设计与实现
- 5Unity3D手游开发实践
- 62023-06-04 Unity ScriptableObject1——ScriptableObject数据文件_代码创建scriptableobject
- 7Axure RP9 ——【内联框架】_axure rp9插入内联框架
- 8【Rust blog】Rust + Flutter 高性能的跨端尝试
- 9窗函数的介绍以及画出常见窗函数(汉宁窗,矩形窗,汉明窗,布莱克曼窗)的时域图和频谱图
- 10超详细YOLOv8实例分割全程概述:环境、训练、验证与预测详解_yolov8环境搭建
机器学习理论笔记(一):初识机器学习
赞
踩

1 前言:蓝色是天的机器学习笔记专栏
尊敬的读者们,大家好!欢迎来到我的全新专栏:《蓝色是天的机器学习笔记》。我感到无比兴奋,能够在这里与各位分享我对机器学习的热爱与探索。这个专栏将成为我记录机器学习知识、交流心得的温馨角落,而这篇文章正是专栏的第一步。
1.1 专栏初衷与定位
作为机器学习领域的狂热爱好者,我一直坚信知识的分享与传播是推动技术进步的关键。《蓝色是天的机器学习笔记》专栏将会是一个持续更新的平台,我将在这里分享我对机器学习领域的理解、学习过程中的心得体会以及实践经验。我希望通过这个专栏,能够与志同道合的你一起探讨机器学习的种种奥秘,共同成长、共同进步。
1.2 本文主要内容
-
机器学习的定义与意义
在机器学习的世界里,计算机不再是被动地执行预设的指令,而是能够通过数据和经验来自主学习、优化性能。机器学习已经渗透到我们生活的方方面面,从智能助理到推荐算法,无不展现出其强大的应用潜力。在本文中,我将为大家详细介绍机器学习的定义及其在现代科技中的重要意义。 -
机器学习的基本术语
在踏入机器学习的领域之前,了解一些基本术语是非常必要的。本文将为大家介绍一些常用的机器学习术语,如监督学习、无监督学习、特征工程等,帮助大家建立起对这些概念的初步认识,为后续的学习打下坚实基础。 -
探索NFL理论
NFL理论,即“没有免费的午餐”定理,是机器学习领域的一项重要原则。它告诉我们,并没有一种算法能够在所有情况下都表现最优,不同的问题需要不同的方法。在本文中,我将解析这一理论的内涵,并探讨其在实际问题中的应用意义。
2 机器学习的定义
在当今信息爆炸的时代,我们每天都在与各种数据打交道。从社交媒体的点赞、购物网站的推荐,到医疗诊断和智能驾驶,我们的世界越来越多地受到数据和技术的影响。但是,如何从这些海量的数据中提取有价值的信息,并做出智能决策,却是一个充满挑战的问题。在这个背景下,机器学习应运而生,为计算机赋予了像人类一样学习和适应的能力。
2.1 机器学习的本质
机器学习是一门让计算机从经验中学习,从而改进性能的学科。它的核心理念可以用一个简单的类比来理解:就像我们根据过去的经验来预测明天的天气,或者在市场上挑选出一个好瓜,机器学习让计算机能够从历史数据中获取“经验”,并通过学习这些经验生成算法模型,从而在面对新的情况时做出有效的判断。
Mitchell的形式化定义
Tom Mitchell,在他的经典教材《机器学习》中,给出了机器学习的形式化定义,它将这一概念表达得更加准确和具体。他将机器学习看作是一个性能改善的过程,通过历史数据的学习来提高计算机程序在某个任务类上的性能。形式化定义中,他引入了三个关键要素:
- P(性能):表示计算机程序在某个任务类T上的表现。这可以是分类准确率、回归误差等,具体取决于任务的性质。
- T(任务类):指计算机程序所要解决的问题类型。这可以是图像识别、自然语言处理等多种任务。
- E(经验):代表历史的数据集,即过去的经验。这些数据将用于训练计算机程序,使其在任务T上表现更好。
根据Mitchell的定义,若计算机程序通过学习经验E,使得在任务T上的性能P得到了改善,那么就可以说该程序对E进行了学习。
2.2 机器学习的分类
机器学习可以分为多个子领域,其中包括但不限于监督学习、无监督学习和强化学习。在监督学习中,计算机从带有标签的数据中学习,以便能够对新数据进行分类或回归。而在无监督学习中,计算机从未标记的数据中发现模式和结构,用于聚类、降维等任务。强化学习则是让计算机在与环境互动的过程中,通过试错来学习最优策略。
3 机器学习的基本术语
在机器学习领域,有许多基本术语用于描述数据、模型以及学习过程,这些术语帮助我们更准确地理解和交流。让我们一起深入探讨这些关键概念。
数据的基本组成
当我们希望让计算机学习的时候,我们首先需要一组数据来作为学习的基础。以西瓜数据为例,每一个记录表示一个西瓜的特征信息:
- 数据集:所有记录的集合称为数据集,它是我们学习的源数据。
- 实例/样本:每一条记录被称为一个实例或样本,它是数据集中的一个单独数据点。
- 特征/属性:数据集中的每个单独特点,比如“色泽”或“敲声”,被称为特征或属性。
- 特征向量:一条记录可以表示为一个特征向量,它是一个在坐标轴上的点,其中每个维度对应一个特征。
训练与测试
在机器学习中,我们需要使用一部分数据来训练模型,然后使用另一部分数据来测试模型的性能:
- 训练样本:用于训练模型的数据样本被称为训练样本,这些样本有标记信息。
- 训练集:所有训练样本的集合被称为训练集,它是用于训练模型的数据集。
- 测试样本:用于测试模型性能的数据样本被称为测试样本,这些样本通常没有标记信息。
- 测试集:所有测试样本的集合被称为测试集,它是用于评估模型性能的数据集。
泛化能力与预测
一个好的机器学习模型应该具有对新数据的适应能力,这就是泛化能力:
- 泛化能力:模型在训练集上的学习成果能够应用到未见过的数据上,这就是模型的泛化能力。
问题类型与学习任务
机器学习可以应用于不同类型的问题,这取决于预测值的性质:
- 分类:当预测值是离散值(如好瓜/差瓜)时,这个问题被称为分类。它可以分为二分类和多分类。
- 回归:当预测值是连续值(如人口数量)时,这个问题被称为回归。
监督学习与无监督学习
根据训练数据是否有标记信息,我们可以将机器学习任务划分为两大类:
- 监督学习:训练数据带有标记信息,包括分类和回归问题。
- 无监督学习:训练数据没有标记信息,包括聚类和关联规则等任务。
4 探索"没有免费的午餐"定理(NFL)
在机器学习领域,有一条被广泛引用的定理,它以简洁的表述揭示了一种普遍的现实:没有免费的午餐(No Free Lunch, NFL)。这一定理的精髓,不仅在机器学习领域有着深刻的应用,同样也适用于我们的个人发展之路。请大家阅读的之前的一篇博文:机器学习中的人生启示:“没有免费的午餐”定理(NFL)的个人发展之道
NFL定理(No Free Lunch Theorem)是机器学习领域的一条基本定理,它通过数学推导提供了深刻的见解。该定理的核心思想是,对于所有问题和所有潜在的学习算法,它们在平均情况下的性能是相同的。这意味着,不存在一种算法可以在所有问题上表现最优。
具体地说,假设我们有一个学习算法集合,表示为A = {A1, A2, … , An},这些算法被应用于不同的问题集合D = {D1, D2, … , Dm}。则NFL定理给出了以下结论:
- 对于特定的问题Di,在某个算法Aj表现良好的情况下,必然存在其他问题Dk,其中算法Aj则表现相对较差。
- 对于任何算法的平均性能,它们在所有问题上的性能都是相同的,即在所有问题上的期望性能相等。
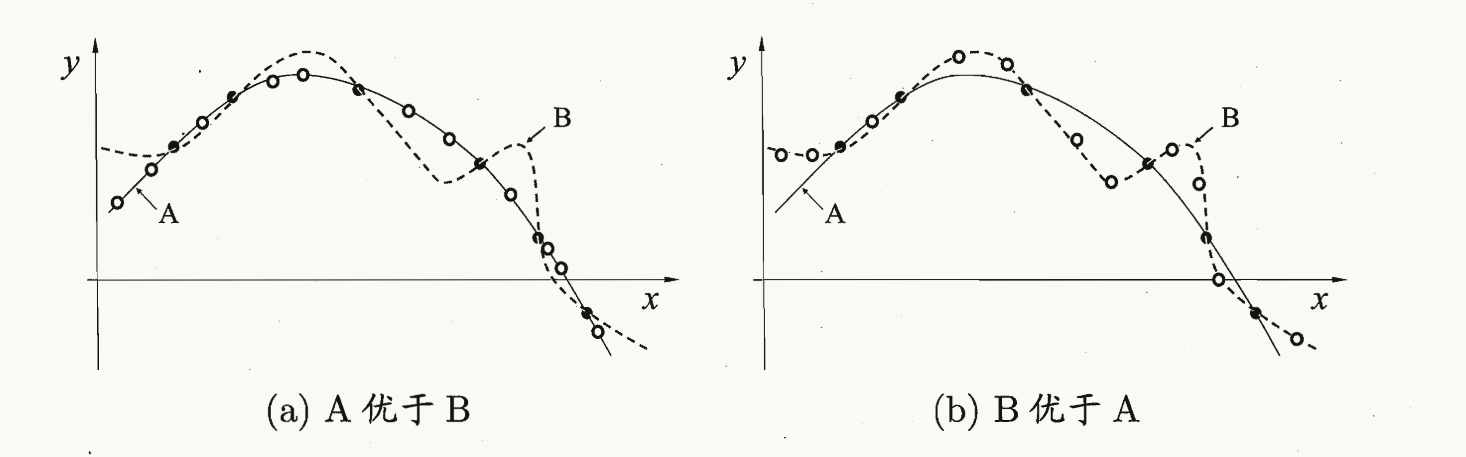
为了更好地理解NFL定理,我们可以通过公式推导进行具体分析。
假设我们有两个算法,算法a和算法b,它们分别用于假设产生和随机猜测。考虑一个离散的样本空间X和假设空间H。我们定义P(h|X,a)为算法a基于训练数据X产生假设h的概率,并假设我们希望找到一个真实目标函数f。那么,算法a在训练集之外的误差可以表示为:

通过公式推导,我们可以清楚地看到NFL定理的数学基础,并理解其中的含义。它提醒我们,没有一种算法可以适用于所有问题,因为问题的特征与算法之间存在着固有的联系。
在个人发展中,我们可以将NFL定理的思想引申到职业选择和发展上。每个人都有自己独特的兴趣、技能和适应能力,没有一种职业或领域适用于所有人。我们需要探索自己的优势并找到适合自己的机会和路径。
无论是在机器学习还是个人发展中,我们都应该理解和接受NFL定理的启示,并通过探索多样的领域来寻找适合自己的机会。这样,我们才能充分发展自己的潜力,并在个人发展中取得成功。让我们一起超越NFL定理的界限,开启个人发展的多彩之旅。
5 结语
在探索机器学习的世界,我们深入研究了"没有免费的午餐"定理(NFL)的重要性,不仅为机器学习带来了新的思考,也为个人发展指明了前进的方向。就像每一种算法在不同问题上都有其优势一样,每个人在人生舞台上也都有独特的闪光点。在机器学习中,我们以数据为驱动,以模型为导航,不断追求优化与创新;在人生中,我们以努力为动力,以梦想为目标,坚定前行,不断突破。无论是解决复杂问题还是实现个人价值,坚持不懈的追求和积极的态度都是成功的关键。
在这篇博文中,我们深入探讨了机器学习的基本术语,剖析了"没有免费的午餐"定理在机器学习和个人发展中的内涵。无论是在选择合适的算法,还是在面对个人发展中的差距感,我们都可以从NFL定理中汲取智慧。正如机器学习中每个问题都需要独特的算法一样,每个人也都有属于自己的人生之路。从学习中汲取经验,不断成长,逐步迈向成功的道路,正是我们共同的努力方向。
让我们在机器学习的探索中,勇往直前;在人生的旅程中,秉持NFL定理的智慧,不断超越自我,创造更加美好的明天。无论是探索科技的边界还是实现个人的梦想,我们都应该坚信:在知识的指引下,没有什么是无法实现的。让我们共同迎接未来的挑战,为机器学习的发展和人生的进步贡献力量,书写属于自己的精彩篇章。



