排序算法——七种排序算法汇总，详细（Java）

排序

排序的概念及应用

排序∶所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的;否则称为不稳定的。

一、直接插入排序

1. 简介

是一种最简单的排序方法，其基本操作是将一条记录插入到已排好的有序表中，从而得到一个新的、记录数量增1的有序表。

2.动图展示

3.过程

1. 将序列中第一个元素看为有序的，将数组划分为有序和无序部分

• 下标i为待排序元素下标，从1开始。n个数需要n-1次遍历。
• j=i-1
  

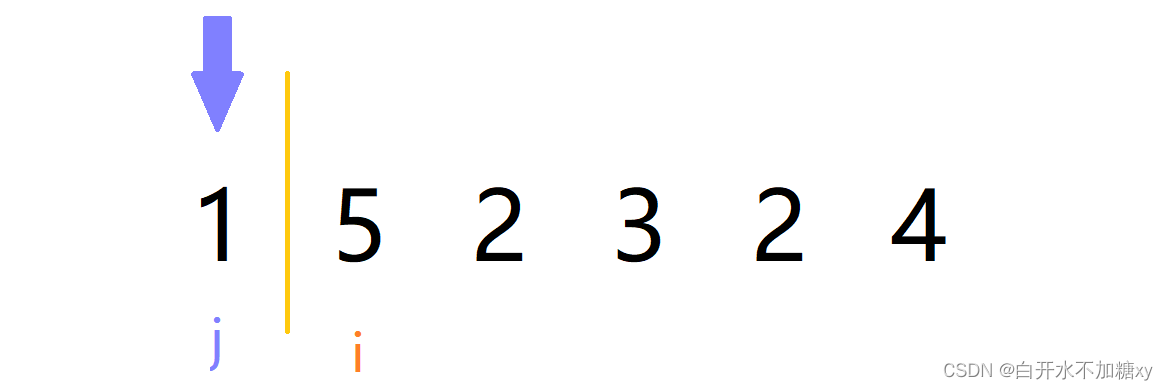
2.每一次插入的比较都是从前一个数开始。即i下标位置待排序元素，与有序部分[0,j]下边处的末尾元素依次向前进行比较

• 若array[i]>array[j]:则array[j+1]=array[i]
  
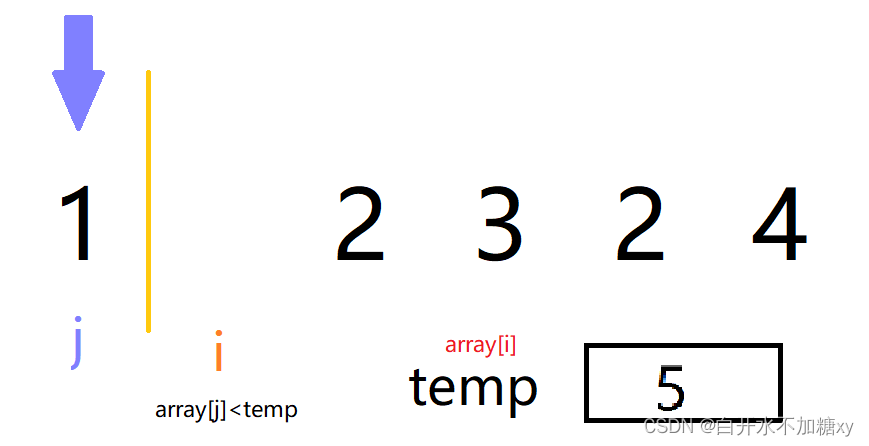
  下标 i 处的元素插入到 j+1 位置。
  

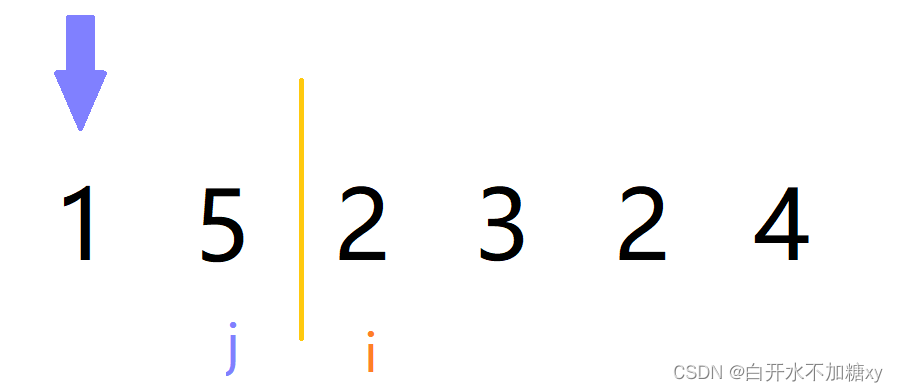
• 若array[i]<array[j]:依次向前遍历有序区间，如果大于取出数，就将这个数后移，j-1
  

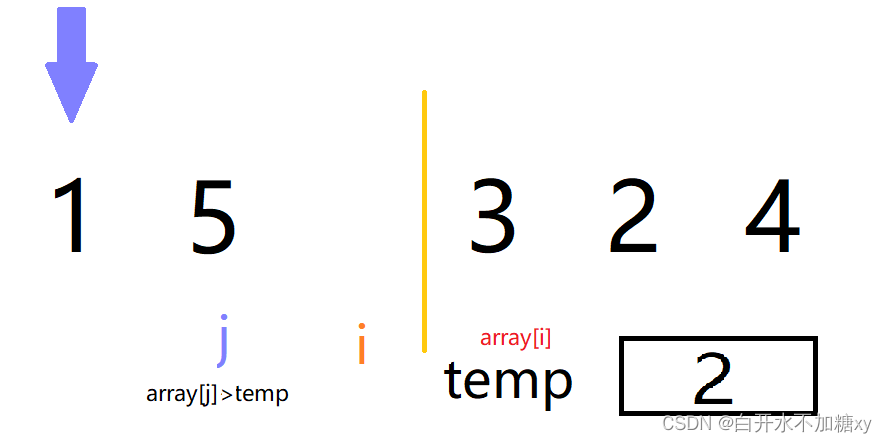
• array[j+1]=array[j] , 执行 j-- 操作
  

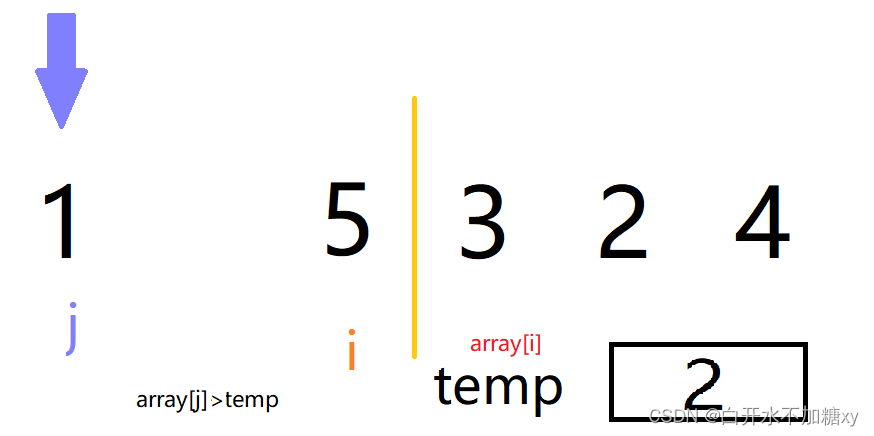
• 不断与 j 下标元素比较，出现小于2的数，找到了插入位置，所以跳出循环，2就可以插入数组了，下标是j+1
  
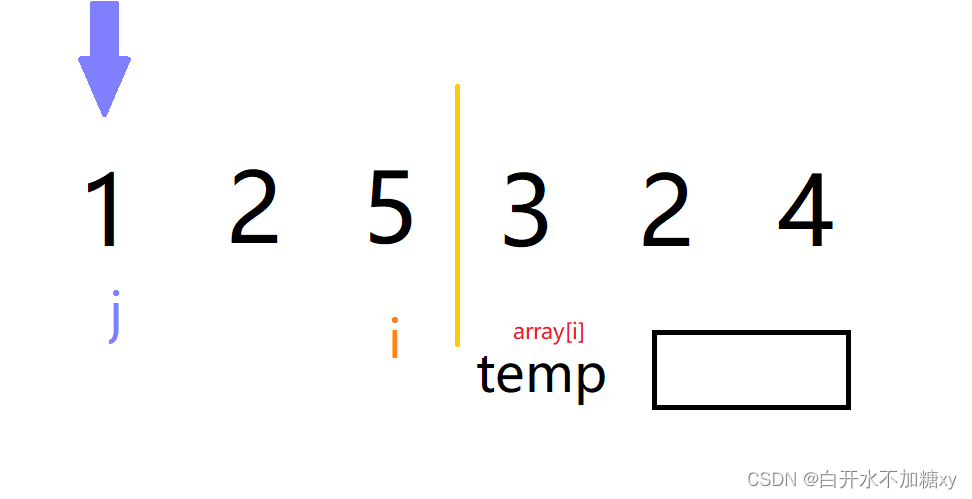
  3.i++，待排序元素更新，同样执行第二步操作，直至无序部分所有元素遍历完成为止
  
  
  
  
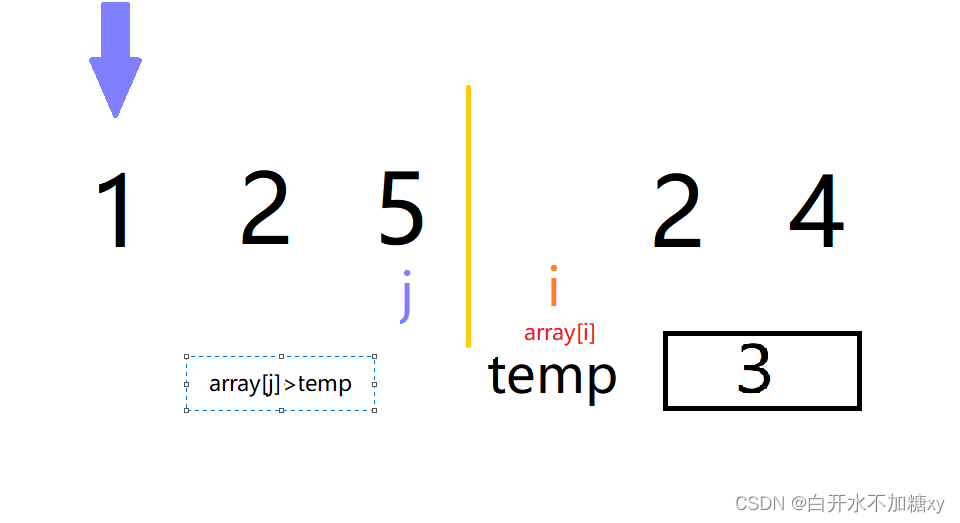
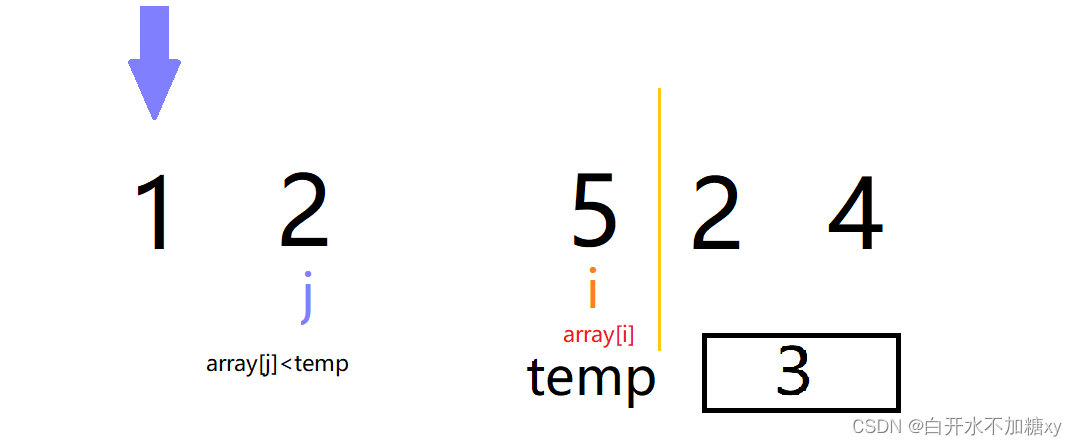
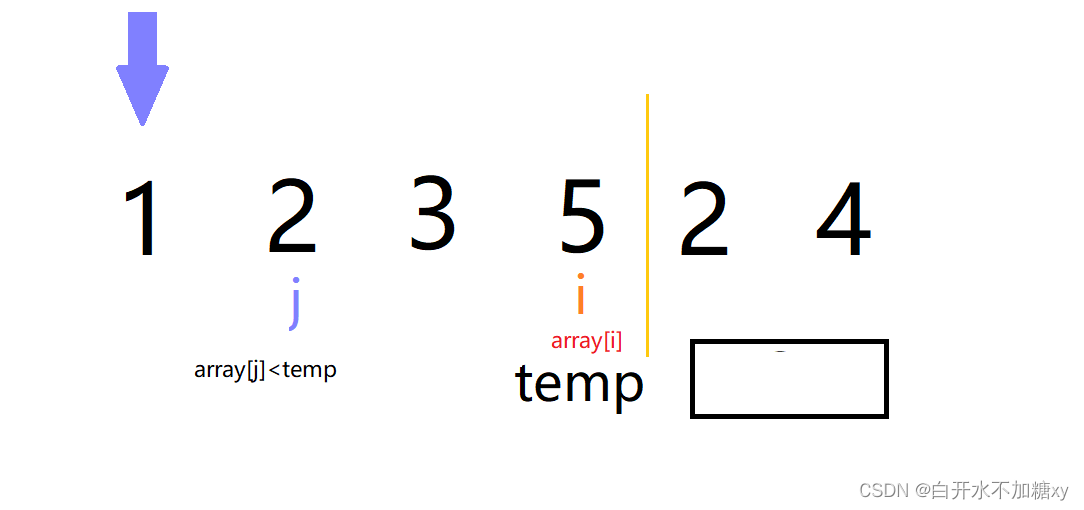
  如上依次操作即可。
  当待排序元素为2时，如下
  
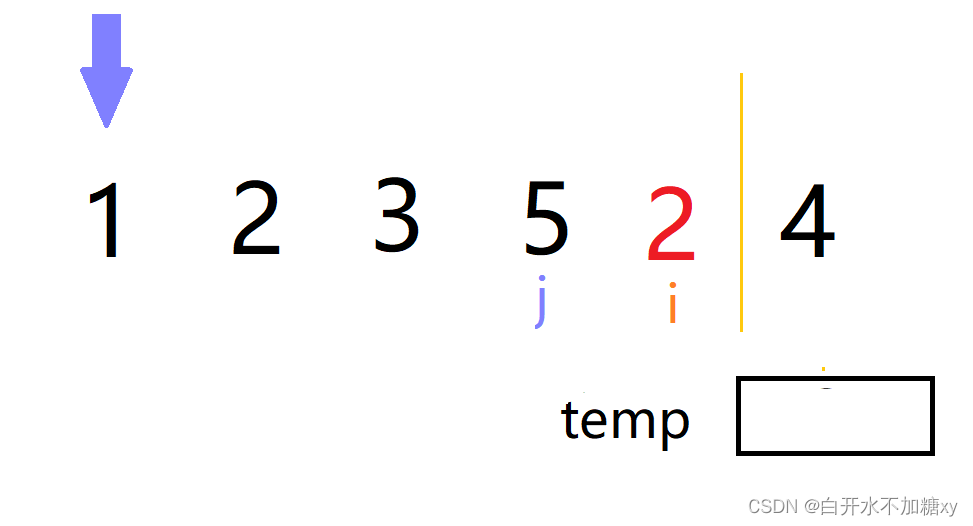
  经过排序插入后结果为如下：
  
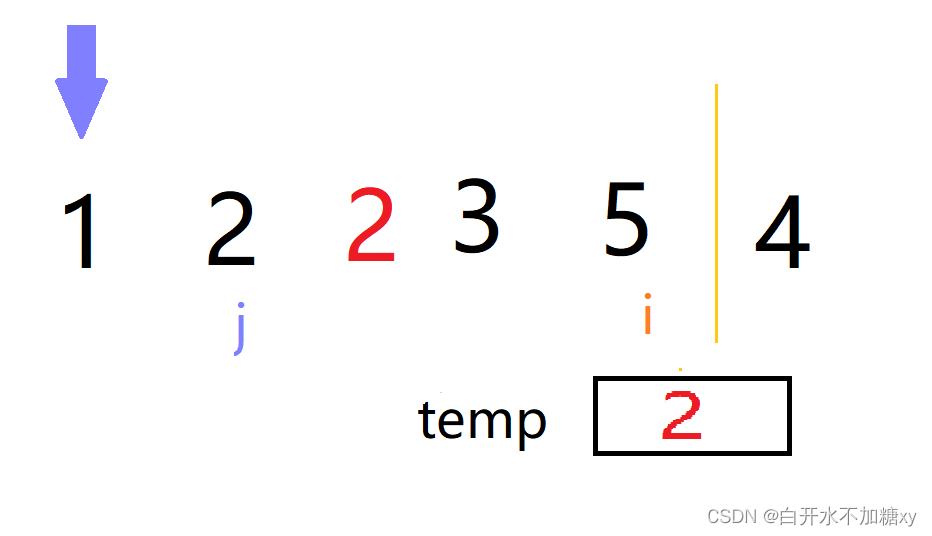
  可见经排序后，两个 2 的相对次序保持不变，说明直接插入排序是稳定的。

4.代码

public class TestSort {


    /**
     * 直接插入排序：
     * 时间复杂度：
     *            最坏情况下：O(N^2)  逆序的
     *            最好情况下：O(N)  有序     如果 以后 数据量不大  而且基本上 趋于有序【优化】
     * 空间复杂度：O(1)
     * 稳定性：稳定
     *
     * 一个本身就稳定的排序，一定也可以实现为不稳定的
     *
     * 但是本身就是不稳定的排序，你能把它变为稳定的排序吗？
     *
     * @param array
     */
    public static void insertSort(int[] array) {

        for (int i = 1; i < array.length; i++) {
            int tmp = array[i];
            int j = i-1;
            for (; j >= 0; j--) {
                //>=
                if(array[j] > tmp) {
                    array[j+1] = array[j];
                }else {
                    //array[j+1] = tmp;
                    break;//
                }
            }
            array[j+1] = tmp;
        }
    }
    public static void main(String[] args) {

        int[] array = {1,5,2,7,9,6,5,7};

        System.out.println("排序前："+Arrays.toString(array));

        insertSort(array);

        System.out.println("排序后："+Arrays.toString(array));
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

5.总结

时间复杂度：

1. 最坏情况下：O(n^2)
2. 最好情况下：O(n) 有序情况下

空间复杂度： O(1)
稳定性： 稳定

二、希尔排序

1.简介

希尔排序法：又称缩小增量法。希尔排序法的基本思想是:先选定一个整数gap，把待排序文件中所有记录分成几个组，所有距离为gap的记录分在同一组内，并对每一组内的记录进行排序。然后，取比上次数小的gap，重复上述分组和排序的工作。当到达=1时，所有记录在统一组内排好序。

2.过程

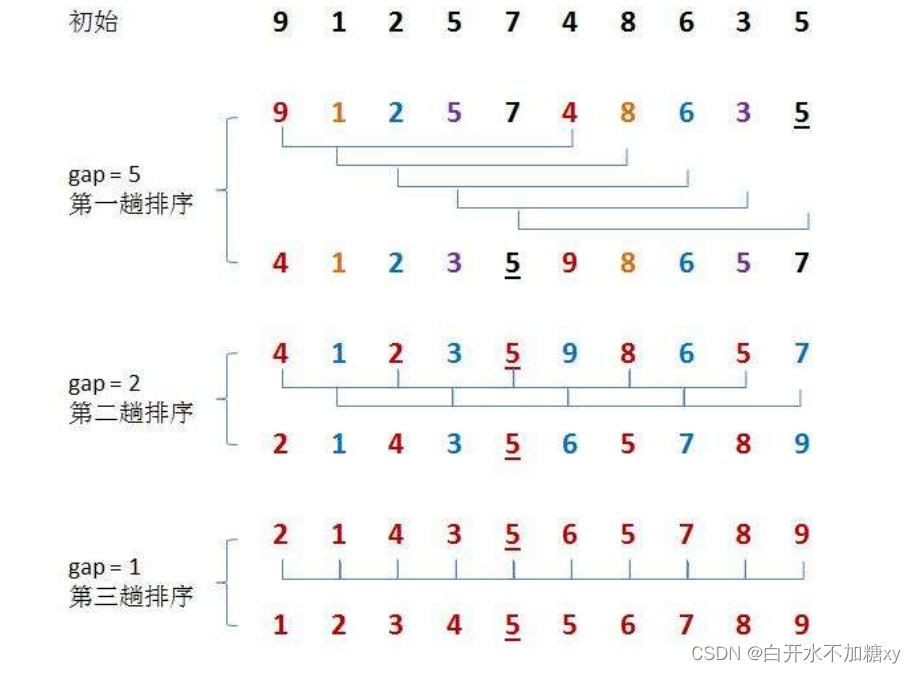
3.代码

import java.util.Arrays;
import java.util.Random;
import java.util.Stack;


public class TestSort {

    /**
     *
     *
     * @param array
     * @param gap
     */
    public static void shell(int[] array,int gap) {

        for (int i = gap; i < array.length; i++) {
            int tmp = array[i];
            int j = i-gap;
            for (; j >= 0; j-=gap) {
                //>=
                if(array[j] > tmp) {
                    array[j+gap] = array[j];
                }else {
                    //array[j+1] = tmp;
                    break;//
                }
            }
            array[j+gap] = tmp;
        }
    }

    /**
     * 时间复杂度：
     *
     * 空间复杂度：
     * O(1)
     * 稳定性：
     * 不稳定
     * @param array
     */
    public static void shellSort(int[] array) {
        int gap = array.length;//10
        while (gap > 1) {
            gap /= 2;
            shell(array,gap);
        }
        shell(array,1);
    }


    public static void main(String[] args) {

        int[] array = {1,5,2,7,9,6,5,7};

        System.out.println("排序前："+Arrays.toString(array));

        shellSort(array);

        System.out.println("排序后："+Arrays.toString(array));
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

4.总结

1.希尔排序是对直接插入排序的优化。
2.当gap > 1时都是预排序，目的是让数组更接近于有序。当gap ==1时，数组已经接近有序的了，这样就会很快。这样整体而言，可以达到优化的效果。我们实现后可以进行性能测试的对比。
3.希尔排序的时间复杂度不好计算，需要进行推导，推导出来平均时间复杂度: O(N^1.3)
O(N^2)
4. **空间复杂度：**O(1)
5. 稳定性: 不稳定

三、选择排序

1.简介

每一次 **从待排序的数据元素**中选出最小(或最大)的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

2.代码

import java.util.Arrays;
import java.util.Random;
import java.util.Stack;


public class TestSort {

    /**
     * 选择排序：
     * 时间复杂度：O(N^2)
     * 空间复杂度：O(1)
     * 稳定性： 不稳定
     * @param array
     */
    public static void selectSort(int[] array) {
        for(int i=0;i<array.length;i++){
        	for(int j=i+1;j<array.length;j++){
        		if(array[j]<array[i]){
        			swwap(array,i,j);
        		}
        	}
        }
    }

	public static void selectSort2(int[] array) {
        for(int i=0;i<array.length;i++){
        	int minIndex=i;//记录 最小值的下标
        	int j=i+1;
        	for(;j<array.length;j++){
        		if(array[j]<array[minIndex]){
        			minIndex=j;
        		}
        	}
        	swwap(array,i,minIndex);
        }
    }

	public static void swap(int[] array,int i,int j){
		int temp=array[i];
		array[i]=array[j];
		array[j]=temp;
	}
    public static void main(String[] args) {

        int[] array = {1,5,2,7,9,6,5,7};

        System.out.println("排序前："+Arrays.toString(array));

        selectSort(array);

        System.out.println("排序后："+Arrays.toString(array));
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

3.总结

时间复杂度： O(n^2)

空间复杂度： O(1)

稳定性： 不稳定

四、堆排序

1.代码

import java.util.Arrays;
import java.util.Random;
import java.util.Stack;


public class TestSort {

    /**
     * 堆排序
     * 时间复杂度：O(n*logn)  和数据有序无序无关
     * 空间复杂度：O(1)
     * 稳定性：不稳定
     * @param array
     */
    public static void heapSort(int[] array) {
        //1、大根堆 O(N)
        createHeap(array);
        //2、排序O(n*logn)
        int end = array.length-1;
        while (end > 0) {
            swap(array,0,end);
            shiftDown(array,0,end);//向下调整大根堆
            end--;
        }
    }

    private static void createHeap(int[] array) {
        for (int parent = (array.length-1-1)/2; parent >= 0 ; parent--) {
            shiftDown(array,parent,array.length);
        }
    }

    private static void shiftDown(int[] array,int parent,int len) {
        int child = (2*parent)+1;
        while (child < len) {
            if(child+1 < len && array[child] < array[child+1]) {
                child++;//他一定保存的是左右孩子的最大值的下标
            }
            if(array[child] > array[parent]) {
                swap(array,child,parent);
                parent = child;
                child = 2*parent+1;
            }else {
                break;
            }
        }
    }
	
	public static void swap(int[] array,int i,int j){
		int temp=array[i];
		array[i]=array[j];
		array[j]=temp;
	}
	
    public static void main(String[] args) {

        int[] array = {1,5,2,7,9,6,5,7};

        System.out.println("排序前："+Arrays.toString(array));

        heapSort(array);

        System.out.println("排序后："+Arrays.toString(array));
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65

2.总结

时间复杂度： O(n*logn) 和数据有序无序无关

空间复杂度： O(1)

**稳定性：**不稳定

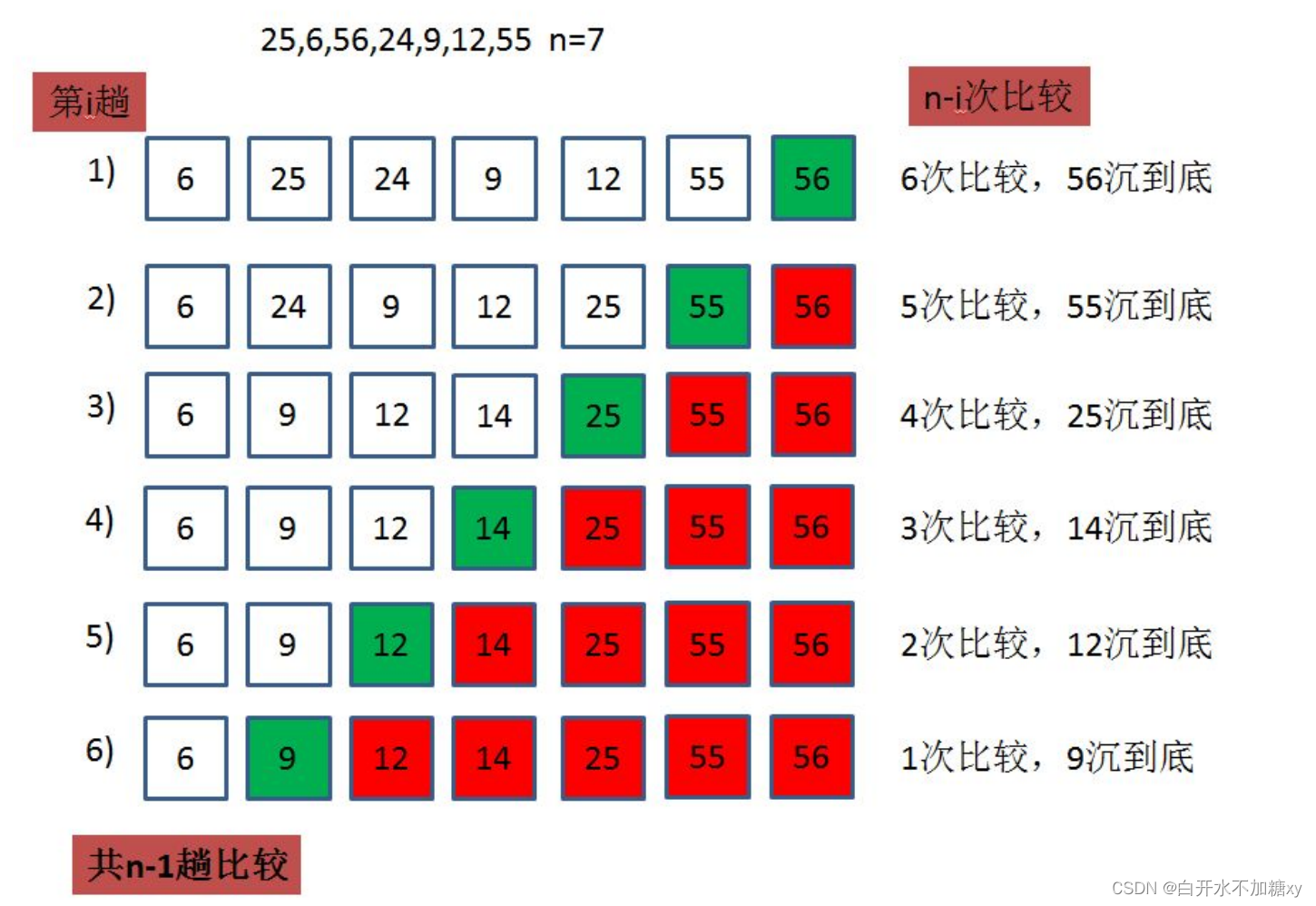
五、冒泡排序

1.过程

2.代码

import java.util.Arrays;
import java.util.Random;
import java.util.Stack;


public class TestSort {

    /**
     * 冒泡排序
     * 不针对优化：
     * 时间复杂度：O(N^2)
     * 空间复杂度：O(1)
     * 稳定性：稳定
     * @param array
     */
    public static void bubbleSort(int[] array) {

        for (int i = 0; i < array.length-1; i++) {
            //boolean flg = false;
            for (int j = 0; j < array.length-1-i; j++) {
                if(array[j] > array[j+1]) {
                    swap(array,j,j+1);
                    //flg = true;
                }
            }
            //if(flg == false) {
            //    break;
            //}
        }
    }
	
    public static void main(String[] args) {

        int[] array = {1,5,2,7,9,6,5,7};

        System.out.println("排序前："+Arrays.toString(array));

        bubbleSort(array);

        System.out.println("排序后："+Arrays.toString(array));
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

3.总结

时间复杂度： O(N^2)

空间复杂度： O(1)

稳定性： 稳定

六、快速排序

1.简介

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为∶任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后左右子序列重复该过程，直到所有元素都排列在相应位置上为止。将区间按照基准值划分为左右两半部分的常见方式有:

1. hoare版本
2. 挖坑法
3. 前后指针版本

分而治之的思想，它的排序过程是一个递归调用的过程。

2.过程

一趟排序过程如下,

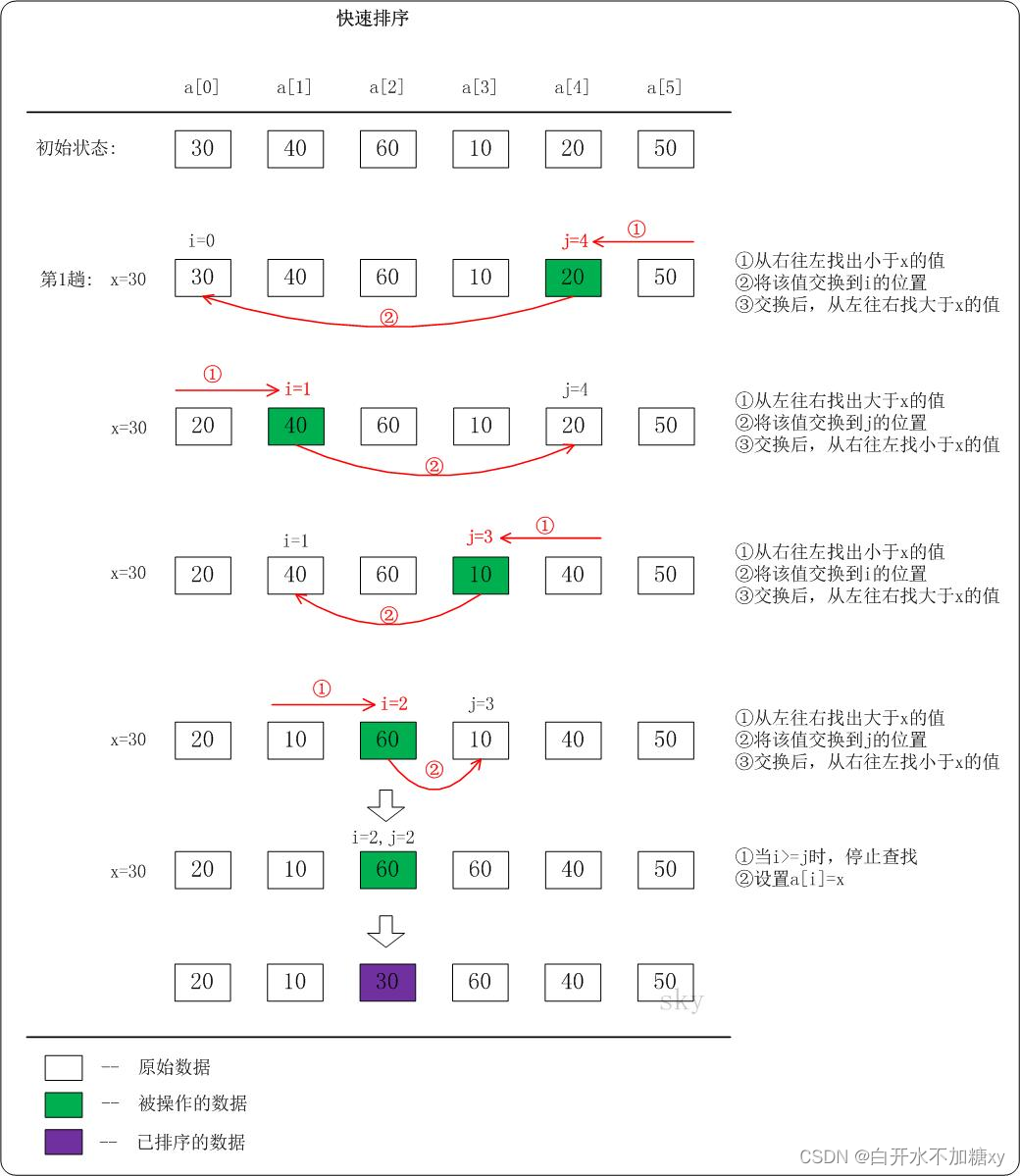
从上图可以看到，完整的快速排序是建立在一趟快速排序之上的，它的具体步骤如下：

1. 首先对待排序序列进行一趟快速排序；
2. 一趟排序下来之后，基准元素（如30)的左边都是比它小的元素，右边都是比它大的元素；
3. 再对基准元素左边的序列进行快速排序，对右边也进行快速排序；
4. 重复步骤2、3，直到序列排序完成。

3.两种优化快速排序的思想

1.三数取中
面对完全有序的数组，快速排序每趟排序后，key的位置都在边缘，每层递归都只能固定一个数，时间复杂度变成了O(N^2)。

面对这种情况，我们可以在取key时动手脚。每次取key我们不再只取最左或最右的值。而是对比最左、最右、中间的三个元素，取三个元素中，值在另外两者中间的元素作为key。这样，就打乱了有序数组，大大加快了快速排序在面对这种情况时的速度。

2.小区间优化
快速排序对一个元素不多的数组排序，仍需要进行多次递归调用，我们知道递归是比较消耗资源的，所以为了避免在快速排序递归的最后几层大量调用函数，我们可以在数组元素较少时不再递归，而是采用直接插入排序替代，这样就能在不损失多少速度的情况下减少大量的递归次数，达到优化速度的目的。

4.代码-递归、非递归、优化

```java
import java.util.Arrays;
import java.util.Random;
import java.util.Stack;


public class TestSort {

    /**
     * 快速排序：
     *
     * 时间复杂度：
     *     最好情况：O(n*logn)  可以每次 尽量将待排序序列 均匀的分割
     *     最坏情况：O(n^2)  正序  逆序
     * 空间复杂度：
     *    最好情况：O(logn)
     *    最坏情况：O(N)
     *
     *  稳定性：不稳定的排序
     *
     * @param array
     */
    public static void quickSort1(int[] array) {
        quick(array,0,array.length-1);
    }

    /**
     * 三数取中法
     * @param array
     * @param left
     * @param right
     * @return 三个数中的 中间数字的下标
     */
    private static int threeMid(int[] array,int left,int right) {
        int mid = (left+right) >>> 1;
        if(array[left] < array[right]) {
            if(array[mid] < array[left]) {
                return left;
            }else if(array[mid] > array[right]) {
                return right;
            }else {
                return mid;
            }
        }else {
            // array[left] > array[right]
            if(array[mid] < array[right]) {
                return right;
            }else if(array[mid] > array[left]) {
                return left;
            }else {
                return mid;
            }
        }
    }


    /**
     *
     * @param array
     */
    private static void insertSort2(int[] array,int start,int end) {

        for (int i = start+1 ; i <= end; i++) {
            int tmp = array[i];
            int j = i-1;
            for (; j >= start; j--) {
                //>=
                if(array[j] > tmp) {
                    array[j+1] = array[j];
                }else {
                    //array[j+1] = tmp;
                    break;//
                }
            }
            array[j+1] = tmp;
        }
    }



    private static void quick(int[] array,int start,int end) {
        if(start >= end) {
            return;
        }
		
		//递归到小区间时，插入排序
        if(end-start+1 <= Constant.INSERT_SIZE) {
            //插入排序
            insertSort2(array, start, end);
            return;
        }

        //三数取中法-》start  end  mid 找到中间的数字
        //有序数据下的优化
        int index = threeMid(array,start,end);
        swap(array,index, start);

        int pivot = partition(array,start,end);
        quick(array,start,pivot-1);
        quick(array,pivot+1,end);
    }


    /**
     * 快速排序：非递归实现
     * @param array
     */
    public static void quickSort(int[] array) {
        Stack<Integer> stack = new Stack<>();

        int start = 0;
        int end = array.length-1;
        int pivot = partition(array,start,end);

        //左边有2个元素及以上
        if(pivot > start+1) {
            stack.push(start);
            stack.push(pivot-1);
        }
        //右边有2个元素及以上
        if(pivot < end-1) {
            stack.push(pivot+1);
            stack.push(end);
        }

        while (!stack.empty()) {
            end = stack.pop();
            start = stack.pop();
            pivot = partition(array,start,end);

            //左边有2个元素及以上
            if(pivot > start+1) {
                stack.push(start);
                stack.push(pivot-1);
            }
            //右边有2个元素及以上
            if(pivot < end-1) {
                stack.push(pivot+1);
                stack.push(end);
            }
        }
    }

    /**
     * 一次划分函数
     * @param array
     * @param left
     * @param right
     * @return
     */
    private static int partition(int[] array,int left,int right) {
        int tmp = array[left];
        while (left < right) {
            //1 2 3 4 5
            while (left < right && array[right] >= tmp) {
                right--;
            }
            //右边 找到小于tmp的数据
            array[left] = array[right];

            while (left < right && array[left] <= tmp) {
                left++;
            }
            //右边 找到小于tmp的数据
            array[right] = array[left];
        }
        array[left] = tmp;
        return left;
    }
	
    public static void main(String[] args) {

        int[] array = new int[10_0000];

        Random random = new Random();

        for (int i = 0; i < array.length; i++) {
            array[i] = i;
            //array[i] = random.nextInt(10_0000);
        }
        long startTime = System.currentTimeMillis();

        quickSort(array);

        long endTimes = System.currentTimeMillis();

        System.out.println(endTimes-startTime);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189

public class Constant {

    public static final int INSERT_SIZE = 100;
}
1
2
3
4

5.总结

时间复杂度：

• 最坏情况下：有序：O(n^2)
• 最好情况下：O(n*logn) 尽量将待排序序列均匀分割

空间复杂度：

• 最坏情况下：O(n)
• 最好情况下：O(logn)

稳定性： 不稳定

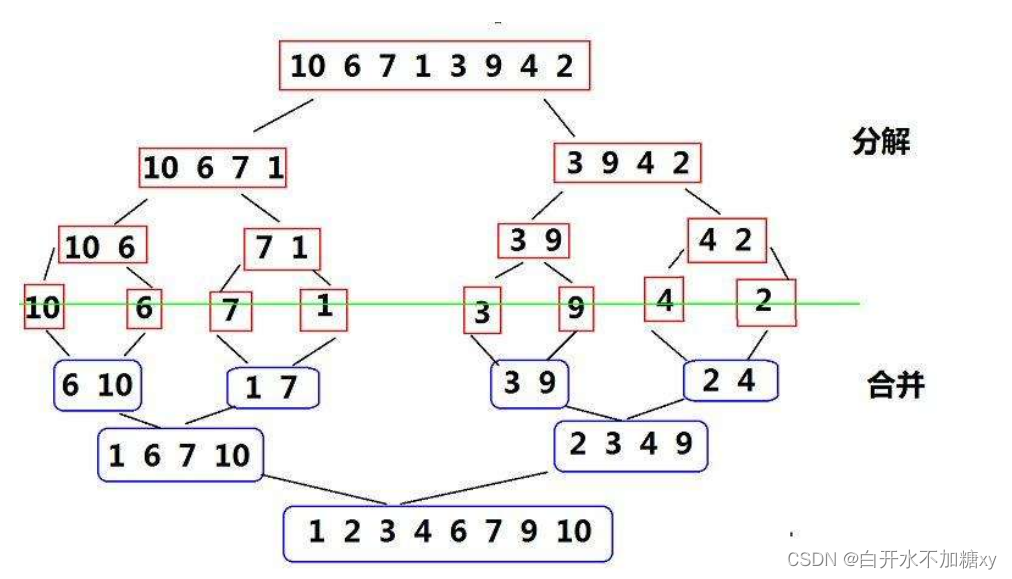
七、归并排序

1.简介

归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide andConquer)的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列;即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。归并排序核心步骤:

2.过程

3.代码

1.递归

/**
     * 归并排序
     * 时间复杂度：n*logn    不管有序还是无序
     * 空间复杂度：O(N)
     * 稳定性：稳定
     *
     * 冒泡   插入  归并
     * @param array
     */
    public static void mergeSort(int[] array) {
        mergeSortFunction(array,0,array.length-1);
    }

    private static void mergeSortFunction(int[] array,int low,int high) {
        if(low >= high) {
            return;
        }
        int mid = (low+high) >>> 1;
        mergeSortFunction(array,low,mid);
        mergeSortFunction(array,mid+1,high);
        merge(array,low,high,mid);
    }
    /**
     * 实现这个合并函数
     * @param array
     * @param low
     * @param high
     * @param mid
     */
    private static void merge(int[] array,int low,int high,int mid) {
        int[] tmp = new int[high-low+1];
        int k = 0;
        int s1 = low;
        int e1 = mid;
        int s2 = mid+1;
        int e2 = high;
        while (s1 <= e1 && s2 <= e2) {
            //两个归并段  都有数据
            if(array[s1] <= array[s2]) {
                tmp[k++] = array[s1++];
            }else {
                tmp[k++] = array[s2++];
            }
        }
        while (s1 <= e1) {
            tmp[k++] = array[s1++];
        }
        while (s2 <= e2) {
            tmp[k++] = array[s2++];
        }
        for (int i = 0; i < k; i++) {
            array[i+low] = tmp[i];
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

2.非递归

    /**
     * 归并排序 ：非递归
     * @param array
     */
    public static void mergeSort2(int[] array) {
        int gap = 1;
        while (gap < array.length) {
            for (int i = 0; i < array.length; i += gap*2 ) {
                int low = i;
                int mid = low+gap-1;
                if(mid >= array.length) {
                    mid = array.length-1;
                }
                int high = mid+gap;
                if(high >= array.length) {
                    high = array.length-1;
                }
                merge(array,low,high,mid);
            }
            gap = gap*2;
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

海量数据排序问题

概念

内部排序:数据在内存上
外部排序:排序过程需要在磁盘等外部存储进行的排序
前提: 内存有1G，需要排序的数据有100G
因为内存中因为无法把所有数据全部放下，所以需要外部排序，而归并排序是最常用的外部排序

过程

1. 先把文件切分成200份，每个512 M
2. 分别对512M排序，因为内存已经可以放的下，所以任意排序方式都可以
3. 200份文件进行2路归并，同时对200份有序文件做归并过程，最终结果就有序了