动手实现线性回归_根据本关卡所学知识,构建线性回归算法,并利用波士顿房价数据对模型进行训练,然后

数据挖掘算法原理与实践：线性回归（房价预测） 动手实现线性回归 201201

答案 educoder

任务描述

本关任务：根据本关卡所学知识，构建线性回归算法，并利用波士顿房价数据对模型进行训练，然后对未知的房价数据进行预测。

相关知识

为了完成本关任务，你需要掌握：1.线性回归算法原理，2.线性回归算法流程。

数据集介绍
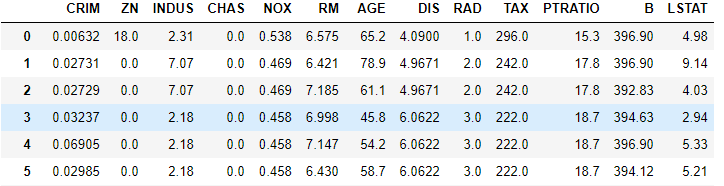
波士顿房价数据集共有506条波斯顿房价的数据，每条数据包括对指定房屋的13项数值型特征和目标房价组成。我们需要通过数据特征来对目标房价进行预测。

数据集中部分数据与标签如下图所示：


sklearn中已经提供了波士顿房价数据集的相关接口，想要使用该数据集可以使用如下代码：

from sklearn import datasets
#加载波斯顿房价数据集
boston = datasets.load_boston()
#X表示特征，y表示目标房价
x = boston.data
y = boston.target
1
2
3
4
5
6

然后再对数据集进行划分：

from sklearn.model_selection import train_test_split
#划分训练集测试集，所有样本的20%作为测试集
train_feature,test_feature,train_label,test_label = train_test_split(x,y,test_size=0.2,random_state=666)
1
2
3

线性回归算法原理

模型训练流程

由数据集可以知道，每一个样本有13个特征与目标房价，而我们要做的事就是通过这13个特征来预测房价，我们可以构建一个多元线性回归模型，来对房价进行预测。模型如下：

其中xi表示第i个特征值，wi​表示第i个特征对应的权重，b表示偏置，y表示目标房价。
为了方便，我们稍微将模型进行变换：

其中x0等于1。

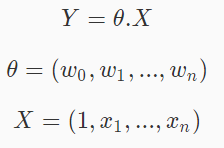
而我们的目的就是找出能够正确预测的多元线性回归模型，即找出正确的参数θ。那么如何寻找呢？通常在监督学习里面都会使用这么一个套路，构造一个损失函数，用来衡量真实值与预测值之间的差异，然后将问题转化为最优化损失函数。既然损失函数是用来衡量真实值与预测值之间的差异那么很多人自然而然的想到了用所有真实值与预测值的差的绝对值来表示损失函数。不过带绝对值的函数不容易求导，所以采用MSE(均方误差)作为损失函数，公式如下：

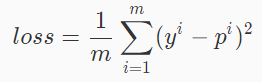
其中p表示预测值，y表示真实值，m为样本总个数，i表示第i个样本。最后，我们再使用正规方程解来求得我们所需要的参数。

线性回归模型训练流程图如下：

正规方程解

对线性回归模型，假设训练集中m个训练样本，每个训练样本中有n个特征，可以使用矩阵的表示方法，预测函数可以写为：

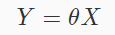
其损失函数可以表示为

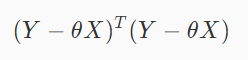
其中，标签Y为mx1的矩阵，训练特征X为mx(n+1)的矩阵，回归系数θ为(n+1)x1的矩阵，对θ求导，并令其导数等于0，可以得到

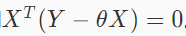
所以，最优解为：

这个就是正规方程解，我们可以通过最优方程解直接求得我们所需要的参数。

线性回归算法流程

我们最终的目的是通过训练出来的线性回归模型对测试集数据进行预测，算法实现流程如下：

将x0=1加入训练数据
使用正规方程解求得参数
将x0=1加入测试数据
对测试集数据进行预测
1
2
3
4

编程要求

根据提示，在右侧编辑器Begin-End处补充 Python 代码，实现线性回归算法与MSE损失函数计算方法，并利用房价数据对模型进行训练，然后对未知的房价数据进行预测。

测试说明

只需返回预测结果即可，程序内部会检测您的代码，MSE低于30则视为过关。

答案代码

#encoding=utf8
import numpy as np

#mse
def mse_score(y_predict,y_test):
    #********* Begin *********#
    ret=(y_test-y_predict)*(y_test-y_predict);
    #********* End *********#
    return ret

def lr(train_feature,train_label,test_feature):
    '''
    input:
        train_feature(ndarray):训练样本特征
        train_label(ndarray):训练样本标签
        test_feature(ndarray):测试样本特征
    output:
        predict(ndarray):测试样本预测标签
    '''
    #********* Begin *********#
    #将x0=1加入训练数据
#seta=np.dot(train_feature.Ttrain_feature)
    #使用正规方程解求得参数

    #将x0=1加入测试数据
    tran = train_feature.T  # (xt)
    linal = np.linalg.inv(np.dot(tran, train_feature)) 
    xtxxt = np.dot(linal, tran)  
    xtxxty = np.dot(xtxxt, train_label)
    seta = xtxxty
    # 使用正规方程解求得参数

    # 将x0=1加入测试数据

    # 求得测试集预测标签
    predict = np.dot(test_feature.all(), seta.all())
    #求得测试集预测标签    

    #********* End *********#
    return predict
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40