【学习打卡04】可解释机器学习笔记之Grad-CAM

可解释机器学习笔记之Grad-CAM

首先非常感谢同济子豪兄拍摄的可解释机器学习公开课，并且免费分享，这门课程，包含人工智能可解释性、显著性分析领域的导论、算法综述、经典论文精读、代码实战、前沿讲座。由B站知名人工智能科普UP主“同济子豪兄”主讲。 课程主页： https://github.com/TommyZihao/zihao_course/blob/main/XAI 一起打开AI的黑盒子，洞悉AI的脑回路和注意力，解释它、了解它、改进它，进而信赖它。知其然，也知其所以然。这里给出链接，倡导大家一起学习， 别忘了给子豪兄点个关注哦。

学习GitHub 内容链接：
https://github.com/TommyZihao/zihao_course/tree/main/XAI

B站视频合集链接：
https://space.bilibili.com/1900783/channel/collectiondetail?sid=713364

Grad-CAM介绍

其实 CAM 得到的效果已经很不错了，但是由于其需要修改网络结构并对模型进行重新训练，这样就导致其应用起来很不方便。

CAM的缺点

1. 必须得有GAP层，否则得修改模型结构后重新训练

2. 只能分析最后一层卷积层输出，无法分析中间层

3. 仅限图像分类任务

Grad-CAM解决了上述问题，基本思路和CAM是一致的，也是通过得到每对特征图对应的权重，最后求一个加权和。区别是求解权重的过程，CAM通过替换全连接层为GAP层，重新训练得到权重，而Grad-CAM另辟蹊径，用梯度的全局平均来计算权重。事实上，经过严格的数学推导，Grad-CAM与CAM计算出来的权重是等价的。

Grad-CAM是CAM的泛化形式

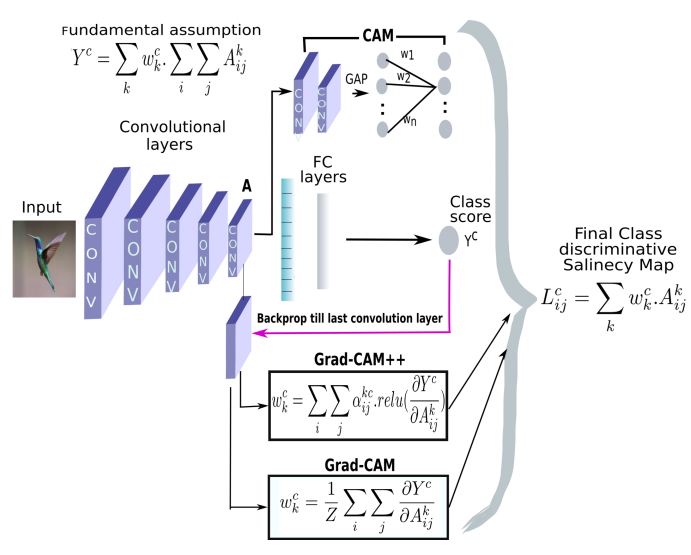
实际上Grad-CAM是CAM的泛化形式，论文中也给出了证明两种方式得到的权重是否等价的详细过程，如果有需要可以阅读论文进行推导。这里为了与 CAM 的权重进行区分，定义 Grad-CAM 中第 k 个特征图对应类别 c 的权重为${\alpha }_k^c$， 可以通过下面的公式计算得到：
$${\alpha }_k^c=\frac{1}{Z}\sum _i\sum _j\frac{\partial y^c}{\partial A_{ij}^k}$$
参数解析：

• Z: 特征图的像素个数；
• $y^c$:第 c 类得分的梯度 (the gradient of the score for class c)；
• $A_{ij}^k$: 第 k 个特征图中，$(i,j)$ 位置处的像素值；

然后再求得所有的特征图对应的类别的权重后进行加权求和，这样便可以得到最后的热力图，求和公式如下：
$$L_{Grad-CAM}^c=ReLU(\sum _k{\alpha }_k^c{A}^k)$$
下图是论文中给出的 Grad-CAM 整体结构图：

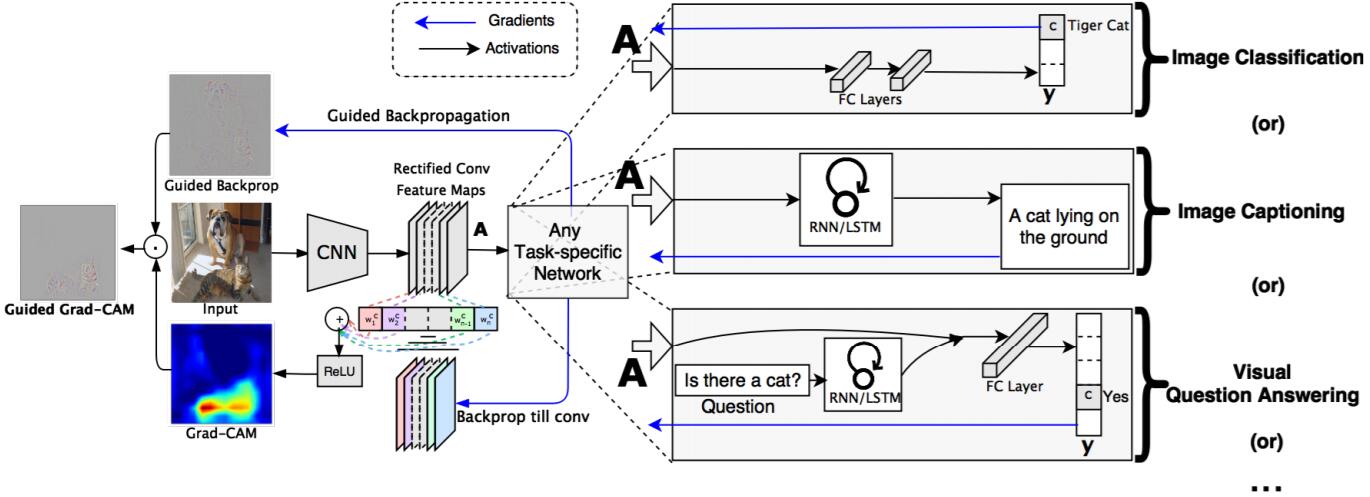
提醒：
论文中对最终的加权结果进行了一次 ReLU 激活处理，目的是只考虑对类别 c 有正影响的像素点。

Gard-CAM可视化结果

可解释性分析

Image captioning task图像语义理解

VQA任务

弱监督定位

弱监督分割

可视化每一层的结果

消除偏见

这个问题非常有意思，在论文6.3章节中举了个非常有意思的例子，作者训练了一个二分类网络，Nurse和Doctor。如下图所示，第一列是预测时输入的原图，第二列是Biased model（具有偏见的模型）通过Grad-CAM绘制的热力图。第三列是Unbiased model（不具偏见的模型）通过Grad-CAM绘制的热力图。通过对比发现，Biased model对于Nurse（护士）这个类别关注的是人的性别，可能模型认为Nurse都是女性，很明显这是带有偏见的。比如第二行第二列这个图，明明是个女Doctor（医生），但Biased model却认为她是Nurse（因为模型关注到这是个女性）。而Unbiased model关注的是Nurse和Doctor使用的工作器具以及服装，明显这更合理。

Grad-CAM算法的优点

1. 无需GAP层，无需修改模型结构，无需重新训练
2. 可分析任意中间层
3. 数学上是原生CAM的推广
4. 细粒度图像分类、Machine Teaching

Grad-CAM算法的缺点

1. 图像上有多个同类物体时，只能画出一块热力图，比如在一张图片有三只猫，他热力图对其中一只猫画热力图
2. 不同位置的梯度值，GAP平均之后，影响是相同的
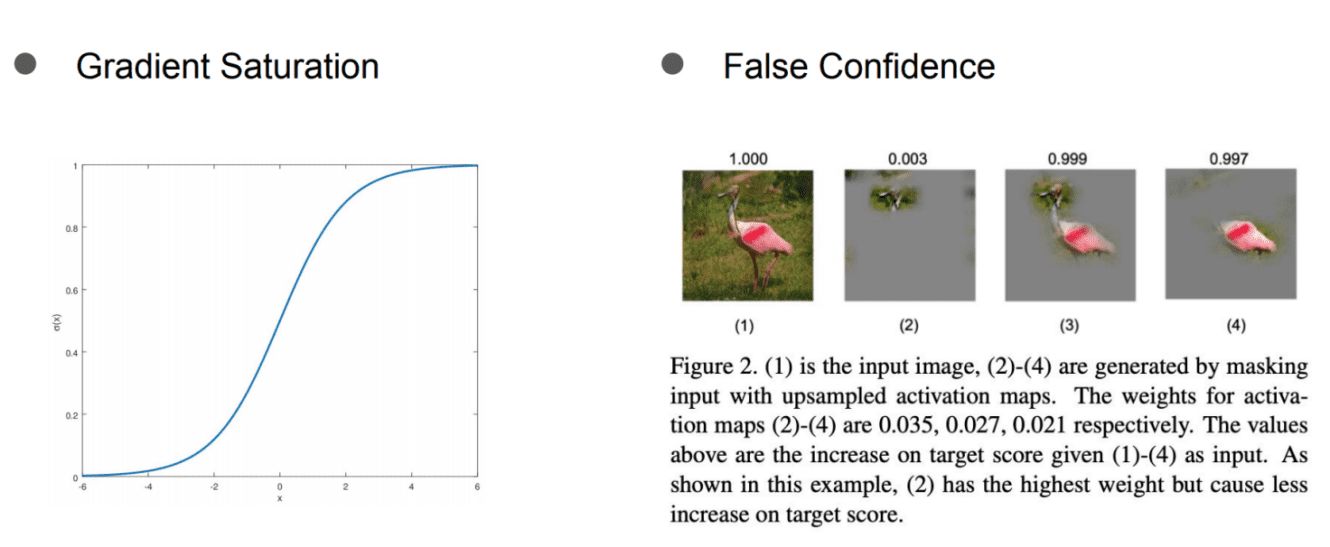
3. 梯度饱和、梯度消失、梯度噪声
4. 权重大的channel，不一定对类别预测分数贡献大
5. 只考虑从后往前的反向传播梯度，没考虑前向预测的影响
6. 深层生成的粗粒度热力图和浅层生成的细粒度热力图 都不够精准

Grad-CAM变种

在后续的发展中，刚刚介绍了Grad-CAM的缺点，而下面的变种就是为了解决上述的六个缺点的。

Grad-CAM++

Grad-CAM++相比Grad-CAM，定位更准确，能够适用于一张图片中的同类多目标的情况，也就是解决了上述第一个缺点

Grad-CAM++的提出是为了优化Grad-CAM的结果，定位会更精准，也更适用于目标类别物体在图像中不止一个的情况。Grad-CAM是利用目标特征图的梯度求平均(GAP)获取特征图权重，可以看做梯度map上每一个元素的贡献是一样。而本文认为梯度map上的「每一个元素的贡献不同」，因此增加了一个额外的权重对梯度map上的元素进行加权。

除此之外，还可以解决第二个缺点，通过基于每个梯度对应的权重，这样就不会导致不同位置的梯度值，GAP以后是一样的，比如中间的和角落位置的肯定是不同的。

Score-CAM

Score-CAM的方法是解决了以上的3,4,5缺点，首先对于第3个缺点，只要有求梯度，一般都会出现梯度的问题，可能来源于梯度本身，即梯度的饱和性（类似于Sigmoid函数，当特征强度超过一定程度，其梯度可能会变小），以及梯度本身的不稳定性（局部的梯度受噪声影响很大），甚至是梯度消失的影响。有可能出现关于输入的梯度或内部层激活可能在视觉上是有噪音的。而可以看到Score-CAM相较于此前的方法，可视化的结果明显更为聚焦，背景中的噪声减少。

除此之外，第四个缺点是权重大的channel，不一定对类别预测分数贡献大，这是因为有时候激活是不一定大的。

以及除了关注反向传播的梯度之外，也涉及了前向传播，通过设计以下的模型，Score-CAM也解决了第五个缺点。

Layer-CAM

还有就是最后的Layer-CAM，他解决了上述问题的第六个缺点，也就是深层生成的粗粒度热力图和浅层生成的细粒度热力图都不够精准，从下图我们可以看出，结果非常的好，甚至可以用来做分割任务了，从浅到深是越来越粗粒度的。

思考与总结

• Grad-CAM有哪些应用? (提示:缺陷检测、弱监督定位、细粒度分类)
• Grad-CAM相比CAM有哪些改进?
• Grad-CAM和CAM为什么在数学上是等价的 ?
• 取不同层做Grad-CAM可解释性分析，效果会有何不同 ?
• 强化学习如何使用Grad-CAM做可解释性分析?
• Grad-CAM有什么缺点?如何改进 ?
• Grad-CAM++对Grad-CAM做了哪些改进?
• ScoreCAM对Grad-CAM做了哪些改进?
• LayerCAM对Grad-CAM做了哪些改进?
• 你是否能想出更好的基于CAM的显著性分析方法?

看了大概的Grad-CAM，感觉上，GradCAM优点就是效果好，改进了CAM；缺点应该是在一张图片中存在多个相同物体的情况下，可能效果会不太好。但是不可否认的是，这种应用的前景广阔，比如在寻找对于网络最敏感的区域上，特别是说在一些machine teaching的任务上，比如缺陷检测中，因为标注成本是非常大的，但是有了Grad-CAM可以迅速寻找对于网络敏感的区域，那些区域可能就是缺陷的区域。

Grad-CAM的缺点上述已经列出来了，之后出现的Grad-CAM的变种Grad-CAM++，ScoreCAM，LayerCAM分别对Grad-CAM的三个缺点进行了改进，使得得到更好的结果。

从现在开始，我们只需要少量的代码，利用Grad-CAM，就可以识别对神经网络模型特征提取图实现可视化，然后使我们清楚地看到神经网络究竟是根据图像的那部分特征进行识别的，对我们的帮助是特别大的，减少了大量的训练成本。我觉得Grad-CAM在CAM的基础上，拥有了更好的泛化性，是非常make sense的，在学习之余，我也不禁开始惊呼，有时候我所认为的黑箱子，还能玩出这么有趣的东西，并且我认为，他们在弱监督的学习上，必将占据一席之地。

参考阅读

• 可以根据按照代码教程:https://github.com/TommyZihao/Train_Custom_Dataset，用pytorch训练自己的图像分类模型，基于torch-cam实现各个类别、单张图像、视频文件、摄像头实时画面的CAM可视化

• Grad-CAM官方代码:https://github.com/ramprs/grad-cam

• torch-cam代码库:https://github.com/frgfm/torch-cam

• pytorch-grad-cam代码库:https://github.com/jacobgil/pytorch-grad-cam