null最后如何排序的_数据结构与算法——常见排序算法分享

排序算法分类

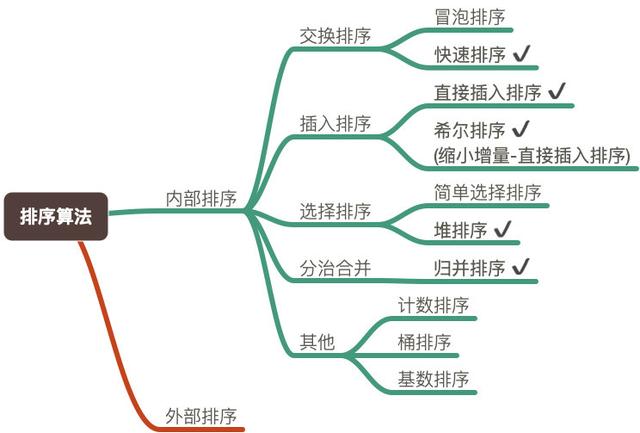
排序算法分类

时间复杂度

各种复杂度效率比较图

O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(2^n) < O(n^3) < O(n^n)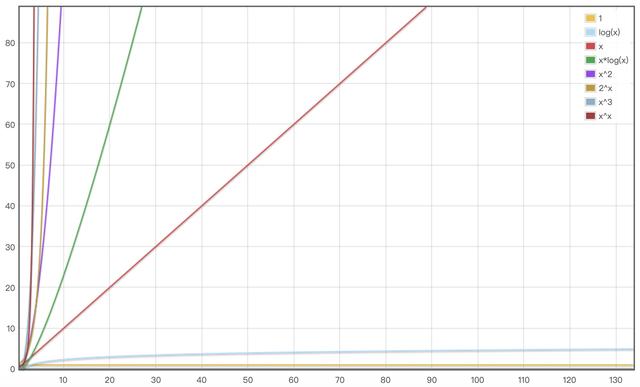

各种时间复杂度效率比较图

说明： n 越大，越能体现算法效率。当 n 比较小时，复杂度会有一波小交叉，上图不考虑 n 比较小的情况。

1. 冒泡排序

public void bubbleSort(int[] array) {    if (array == null) {        return;    }    int temp;    // 冒泡次数    for (int i = array.length - 1; i > 0; i--) {        // 冒泡排序        for (int j = 0; j < i; j++) {            // 将大值交换到后面            if (array[j] > array[j + 1]) {                temp = array[j];                array[j] = array[j + 1];                array[j + 1] = temp;            }        }     }}

2. 快速排序

基本思想：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

public void quickSort(int[] array, int left, int right) {    if (array == null) {        return;    }        if (left < right) {        int i = left;        int j = right;        int temp = array[i]; // 选取一端值为基准值                while (i < j) {            // 如果 j 处值大于等于基准值，那么不用交换数据，直接将 j 向前移动，            // 直到 i 等于 j 或者 j 处值比基准值小            while (i < j && array[j] >= temp) {                j--;            }            // 如果 i < j，说明 j 处值比基准值小(根据上面循环判断)            if (i < j) {                // 交换 j 与 i 处的值，并将 i 向后移动                array[i++] = array[j];            }                                    // 如果 i 处值小于等于基准值，那么将i向后移动就可以了            while (i < j && array[i] <= temp) {                i++;            }            // 如果 i < j，说明 i 处值比基准值大(根据上面循环判断)            if (i < j) {                // 交换 i 与 j 处的值，并将 i 向前移动                array[j--] = array[i];            }                        // 最后将临时基准值填充到 i 处            array[i] = temp;            // 对两段各自快速排序        }                quickSort(array, left, i - 1);        quickSort(array, i + 1, right);    }}

3. 直接插入排序

public void insertionSort(int[] array) {    if (array == null) {        return;    }    // 和冒泡排序有些类似，这里是遍历趟数    for (int i = 0; i < array.length; i++) {        // 精髓是从局部有序，到整体有序        int temp = array[i]; // 当前基准元素        int j;        for (j = i; j > 0 && array[j - 1] > temp; j--) {            array[j] = array[j - 1]; // 下一个元素比基准元素大，下一个元素向后移动        }        // 最后比较当前元素和基准元素大小        if (array[j] > temp) {            array[j] = temp;        }    }}

4. 希尔排序(缩写增量-直接插入排序)

public void shellSort(int[] array) {    if (array == null) {        return;    }    // 计算增量    for (int d = array.length / 2; d > 0; d /= 2) {        // 分组        for (int g = 0; g < d; g++) {            // 插入排序(第 x 组的第 d 个增量元素起步)(直接插入排序的增量是 1，这里是 d，需注意下)            for (int i = g + d; i < array.length; i += d) {                int temp = array[i];                int j;                for (j = i; j > d && array[j - d] > temp; j -= d) {                    array[j] = array[j - d];                }                if (array[j] > temp) {                    array[j] = temp;                }            }        }    }}

5. 简单选择排序

public void selectionSort(int[] array) {    if (array == null) {        return;    }        int index;    int temp;    // 做出的选择次数    for (int i = array.length - 1; i > 0; i--) {        index = 0;        for (int j = 1; j < i; j++) {            // 选择一个最大的值(记录索引)            if (array[j] > array[index]) {                index = j;            }        }        // 将选出的最大值换到一端        if (array[index] > array[i]) {            temp = array[index];            array[index] = array[i];            array[i] = temp;        }    }}

6. 堆排序

public void heapSort(int[] array) {    if (array == null) {        return;    }        for (int i = array.length / 2 - 1; i >= 0; i--) {        // 先调整堆(选择一个最大值放到堆顶)        adjustHeap(array, i, array.length);    }    for (int i = array.length - 1; i > 0; i--) {        // 将堆顶的元素与其他元素比较并交换        swap(array, 0, i);        // 再调整堆        adjustHeap(array, 0, i);    }}// 调整堆，使得堆顶元素值大于等于其子节点值private void adjustHeap(int[] array, int top, int length) {    int temp = array[top];    for (int i = top * 2 + 1; i < length; i = i * 2 + 1) {        // (如果存在的化)从左右子节点找出值最大的子节点        if (i + 1 < length && array[i + 1] > array[i]) {            i++;        }        if (array[i] > temp) {            array[top] = array[i];            top = i;        } else {            break;        }    }        if (array[top] > temp) {        array[top] = temp;       }}private void swap(int[] array, int a, int b) {    int temp = array[a];    array[a] = array[b];    array[b] = temp;}

7. 归并排序

public void mergeSort(int[] array) {    if (array == null) {        return;    }        int[] aux = new int[array.length];    sort(array, 0, array.length - 1, aux);}private void sort(int[] array, int left, int right,int[] aux) {    if (left < right) {        int mid = (left + right) / 2;        // 先分后合        sort(array, left , mid, aux);        sort(array, mid + 1, right, aux);        merge(array, left, mid, right, aux);    }}private void merge(int[] array, int left, int mid, int right, int[] aux){    int t = 0;    int l = left;    int m = mid + 1;        // 判断元素值大小，按大小排序到辅助数组上    while (l <= mid && m <= right) {        if (array[l] <= array[m]) {            aux[t++] = array[l++];        } else {            aux[t++] = array[m++];        }    }        // 把剩余元素填充到辅助数组上    while (l <= mid) {        aux[t++] = array[l++];    }    while (m <= right) {        aux[t++] = array[m++];    }        // 将辅助线数组上的元素复制到需要排序的数组上    t = 0;    while (left <= right) {        array[left++] = aux[t++];    }}