强化学习八、策略梯度_策略梯度更新

到目前为止，前面分享的从MDP到DQN都是值函数的方法，值函数方法的思路是先通过策略评估和策略改善两个步骤优化值函数，然后通过最优的值函数来导出最优的策略，此时的最优策略是贪婪策略，也就是在给定状态s，寻找最大状态值函数的动作，它是一个状态空间到动作空间的有限映射。

其实值函数的方法是有一些局限性的：

      1、策略π是通过值函数产生的，但是有时候值函数很难计算的，比如让机器人打乒乓球，你需要前后左右移动来接球，计算小球在某一个位置是采取什么样的行动是很困难的。

      2、对于高纬度或者连续的状态空间，值函数方法在得到价值函数后，很难通过比较各种动作的价值大小来制定策略。

      3、值函数学习到的策略往往是贪婪的，其实有时候并非是最好的策略，比如我们在玩石头剪刀布游戏的时候，随机策略往往是最好的。

      4、部分值函数在迭代后期会围绕最优价值函数波动而不收敛。

我们回顾一下强化学习的目的：通过智能体与环境的交互来获得累计回报的期望（因为每次交互是随机的，所以求期望）最大，我们定义每次试验所获得的累积回报为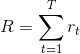，也就是求期望R最大，其实我们可以直接来优化策略使得这个回报最大，这正是策略梯度的思路。策略梯度不是像值函数方法中一样把策略看作是概率集合，而是直接把策略参数化，如下：。

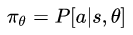首先我们从免模型开始，之前已经介绍过MC和TD两种免模型方法，思路是通过与环境交互来获得样本，然后进行后续的值函数计算，我们现在从极大似然的角度来看策略梯度：

假如有一次试验结果如下：

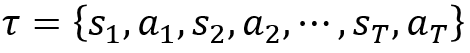
，s表示状态，a表示基于前面状态s采用的动作。那我们计算一下本次试验出现的概率

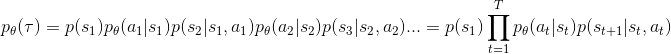
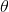表示策略的参数。

那么多次试验的期望回报为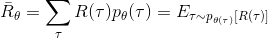：，其中

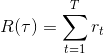，表示每次试验回报总和。现在已经有了策略梯度的目标函数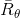，那么只需要求解目标函数的梯度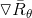即可。

下面详细介绍一下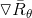的推导过程：

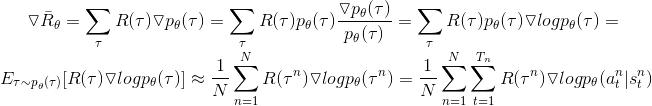
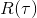不需要是可微分的，是黑箱子。

 

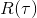控制了参数更新的方向和步长，类似神经网络中的学习率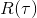，为正且越大，参数更新后该试验出现的概率会越大；反之，会抑制该试验的出现。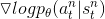是t时刻状态s下采取动作a的概率随参数变化最陡的方向。

公式推导小技巧：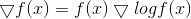

下面我们看一下策略梯度更新的流程和步骤，如下图所示：

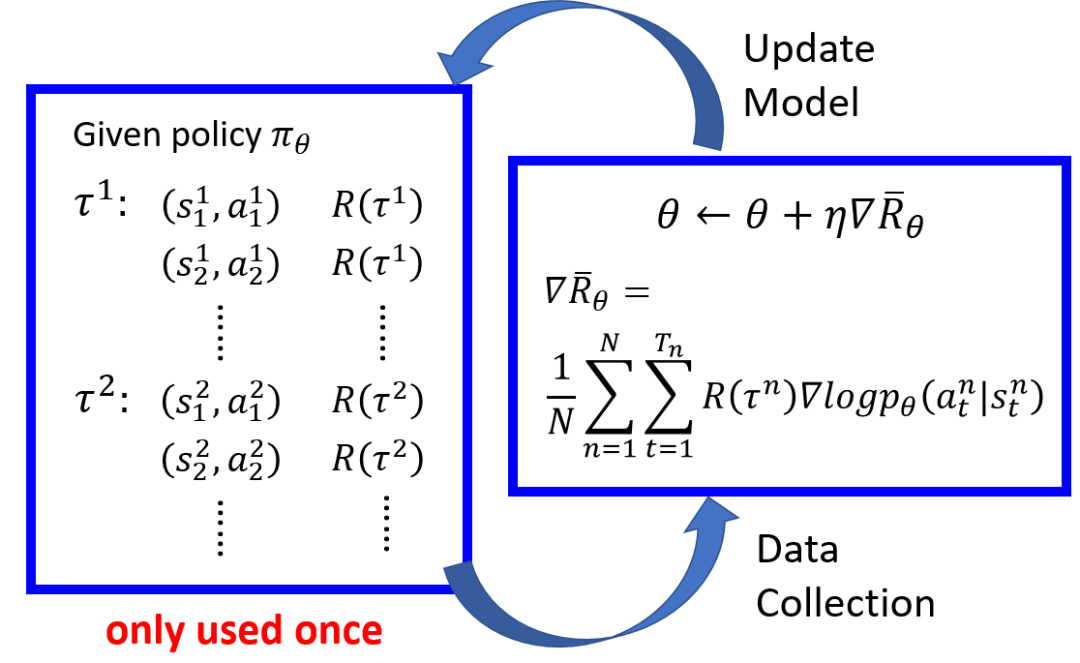
首先根据初始策略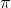与环境交互获取多次试验，由于在每次试验中出现的状态以及对应的动作都是随机的，所以需要把每次试验的状态-动作pair以及获得的总回报记录下来，梯度使用这些试验记录下来的值，根据公式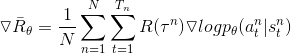计算策略梯度的值，然后使用

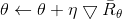来更新策略，更新后，之前策略产生的数据就没用了，可以删除，然后根据新的策略重新与环境交互得到新试验的状态-动作pair以及获得的总回报，重新更新策略，如此往复，直到策略收敛。

策略梯度公式改进：

原梯度更新公式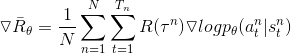：                   （1）

1、从公式（1）看出，如果环境给予的回报始终为正，那么我们无论我们的决策如何，最终的累积的长期回报值都是一个正数。换句话说，我们会增强所有的策略，只是对于实际效果并不好的策略，我们为其提升的幅度有所降低。这样的更新方法和我们的初衷并不一致，我们降低不好行动的概率，而不是轻微提升不好的行动概率。我们可以在累计总回报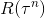上减去一个偏移量b，使得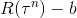在不同的试验中有正有负，修改后公式如下：

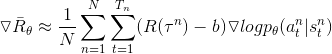                                       （2）

 

最简单的b可以使用所有试验累计回报的期望值，如

2、从修改后公式（2）中我们可以看到一个问题，不论是那个时间段，我们都要用策略的梯度乘以所有时刻的回报值总和，这样的设计显然是不合理的。因为理论上，在t时刻我们完成了决策后，它最多只能影响t时刻之后的所有回报，并不会影响t时刻之前的回报，因为我们无法通过现在的决策影响已经发生过的事情，所以这一部分的回报值不应该计算在梯度中，所以可以做如下修改：

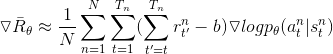                                       （3）

 

3、从公式（3）看出，还有改进空间，直观上讲，未来离当前越远，当前的决定应该对其产生的影响越小，修改如下：

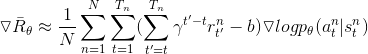
 ，其中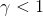

致谢：非常感谢李宏毅老师的视频https://www.bilibili.com/video/av24724071