[ 数据结构 -- 手撕排序算法第七篇 ] 堆、堆排序_堆排序和顺序表

  目录

1.堆的概念结构及分类

1.2堆的分类

1.2.1 大堆

1.2.2 小堆

2. 堆的主要接口

3.堆的实现

3.1 堆的初始化 HeapInit

3.2 堆的销毁 HeapDestory

3.3 堆的打印 HeapPrint

3.4 堆的插入元素 HeapPush   *

功能分析：

功能实现：

3.5 堆的删除元素 HeapPop  *

功能分析:

功能实现:

3.6 判断是否为空 HeapEmpty

3.7 求元素个数

3.8 求堆顶元素

 4.堆的应用：堆排序   ***

4.1 堆排序实现过程分析

4.2 堆排序实现代码

4.3 堆排序结果演示

5.堆(小堆)的完整代码

1.堆的概念结构及分类

以上这段概念描述看起来十分复杂，晦涩难懂。那么堆用通俗语言简单描述如下：

堆是一个完全二叉树的顺序存储。在一个堆中，堆的父节点一定大于等于(或小于等于)子节点。一旦有一部分不满足则不为堆。

堆的性质： 

1、堆中某个节点的值总是不大于或不小于其父节点的值；

2、堆总是一棵完全二叉树

1.2堆的分类

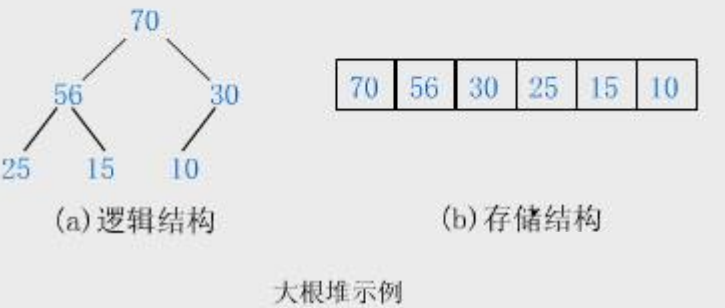
1.2.1 大堆

在一个堆中，父节点一定大于等于子节点的堆称为大堆。又称大根堆。

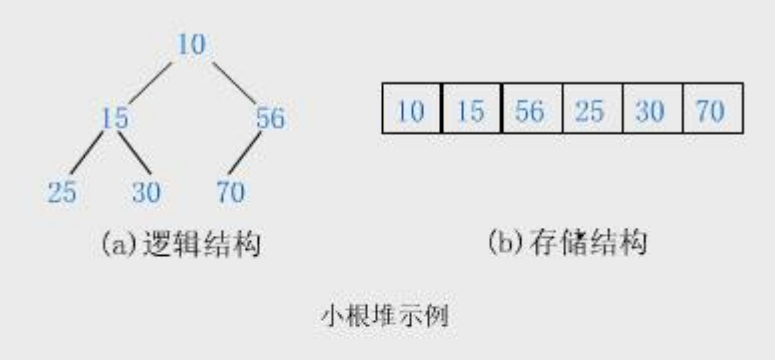
1.2.2 小堆

在一个堆中，父节点一定小于等于子节点的堆称为小堆。又称小根堆。(下图就是一个小堆)

习题练习：

1.下列关键字序列为堆的是：（A）
A 100,60,70,50,32,65
B 60,70,65,50,32,100
C 65,100,70,32,50,60
D 70,65,100,32,50,60
E 32,50,100,70,65,60
F 50,100,70,65,60,32
 

2. 堆的主要接口

在本篇文章中我们主要以小堆为例实现。

现实中我们通常把堆使用顺序结构的数组来存储，需要注意的是这里的堆和操作系统 虚拟进程地址空间中的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段。

其中堆中包括以下主要功能：

1.堆的初始化   2.堆销毁  3.堆打印  4.堆的插入元素  5.堆删除元素   6.判断堆是否为空  7.求堆中元素的个数  8.求堆顶元素

详细接口如下：

//小堆
//算法逻辑思想是二叉树，物理上操作的是数组中数据
typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;   //数组a
	size_t size;     //下标
	size_t capacity; //容量
}HP;
 
void Swap(HPDataType* pa, HPDataType* pb);//交换函数
void HeapInit(HP* php);//堆初始化
void HeapDestory(HP* php);//堆销毁
void HeapPrint(HP* php);//堆打印
 
//插入x以后，仍然要保证堆是（大/小）堆
void HeapPush(HP* php, HPDataType x);
 
//删除堆顶的数据（最大/最小）
void HeapPop(HP* php);
 
bool HeapEmpty(HP* php); //判断是否为空
size_t HeapSize(HP* php);//求元素个数
HPDataType HeapTop(HP* php);//求堆顶元素

3.堆的实现

有了如上的接口，接下来我们实现各个接口。由于我们使用数组来实现堆，大多接口功能和顺序表的实现相同。相同的实现这里不再过多分析。

3.1 堆的初始化 HeapInit

void HeapInit(HP* php)
{
	assert(php);
	php->a = NULL;
	php->size = php->capacity = 0;
 
}

3.2 堆的销毁 HeapDestory

void HeapDestory(HP* php)
{
	assert(php);
	free(php->a);
	php->a = NULL;
	php->capacity = php->size = 0;
 
}

3.3 堆的打印 HeapPrint

void HeapPrint(HP* php)
{
	assert(php);
	for (size_t i = 0; i < php->size; ++i)
	{
		printf("%d ", php->a[i]);
	}
	printf("\n");
}

3.4 堆的插入元素 HeapPush   *

堆的元素插入是堆的一大重点和难点。接下来我们对该功能进行分析和实现。

功能分析：

1、我们要向堆中插入元素，我们首先要判断数组是否空间已满，如果空间已满就要扩容。扩容后再将新元素插入数组尾部。此过程和顺序表相同。

2、由于插入新元素，我们要对该元素进行分析（此处以如下图小堆举例），分析插入元素是否会破坏堆结构，如果破坏了堆，我们就要对堆进行向上调整。

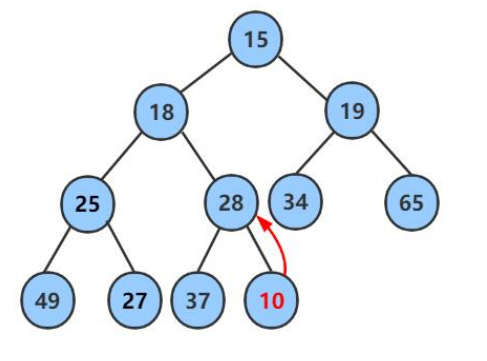
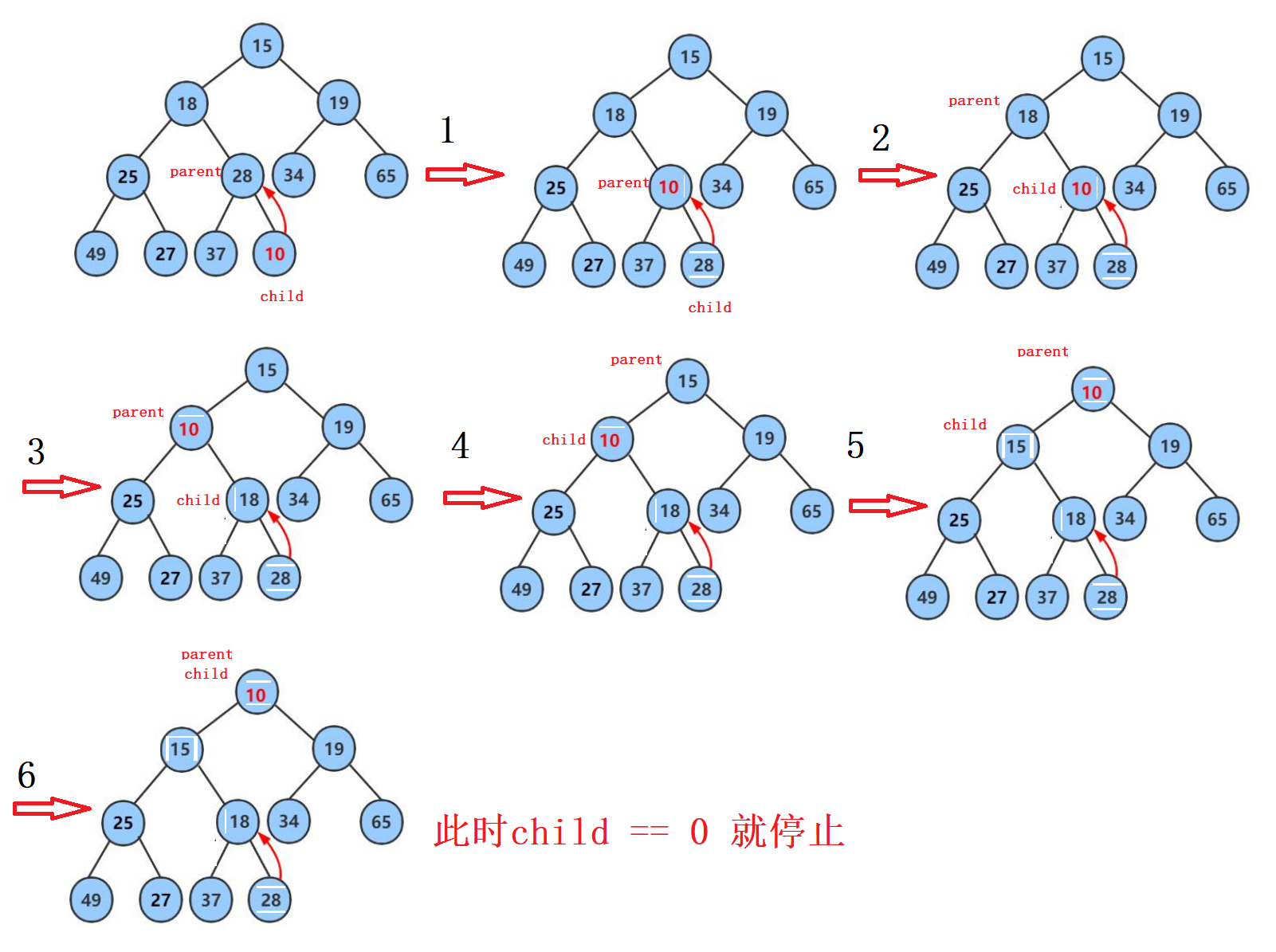
3、向上调整过程分析(过程步骤如下图)：

a. 我们发现出入新元素10之后，10作为28(父节点)的子节点却比28小，这样就破坏了我们的堆结构，这样就不构成小堆。因此我们需要对该结构进行调整。

b.由于堆的物理结构是一个数组，所以我们可以通过数组下标的形式找到我们孩子节点的父节点。不难分析出parent = (child-1)/2.当我们找到父节点时，我们进行大小比较，如果子节点小于父节点，此时就要进行交换元素。再让子节点到父节点的位置，重新计算父节点。

c.持续循环比较，如果child等于0时，说明向上调整结束。因此循环的条件可写为child>0.

注：循环过程中一旦成堆，则跳出循环。

功能实现：

//交换函数
void Swap(HPDataType* pa, HPDataType* pb)
{
	HPDataType tmp = *pa;
	*pa = *pb;
	*pb = tmp;
}
 
 
//向上调整
void AdjustUp(HPDataType* a, size_t child)
{
	size_t parent = (child - 1) / 2;
	while (child > 0)
	{
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}
 
 
void HeapPush(HP* php, HPDataType x)
{
	assert(php);
	//考虑是否扩容
	if (php->size == php->capacity)
	{
		size_t newCapacity = php->capacity == 0 ? 4 : php->capacity * 2;
		HPDataType* tmp = realloc(php->a, sizeof(HPDataType) * newCapacity);
		if (tmp == NULL)
		{
			printf("realloc failed\n");
			exit(-1);
		}
		php->a = tmp;
		php->capacity = newCapacity;
	}
	php->a[php->size] = x;
	++php->size;
	//需要向上调整
	AdjustUp(php->a, php->size - 1);
}

3.5 堆的删除元素 HeapPop  *

删除堆是删除堆顶的数据

思路：将堆顶的数据跟最后一个数据一换，然后删除数组最后一个数据，再进行向下调整算法。

功能分析:

我们要删除堆是删除堆顶的数据，我们不能直接删除堆顶的数据。如果直接删除堆顶的数据，就会破坏堆结构，并且复原的复杂度较高。在这里我们介绍一种方法不仅解决了删除堆的问题，并且复杂度较低。

1、首先我们要将堆顶的数据跟最后一个数据交换，然后删除数组最后一个数据，再进行向下调整算法。

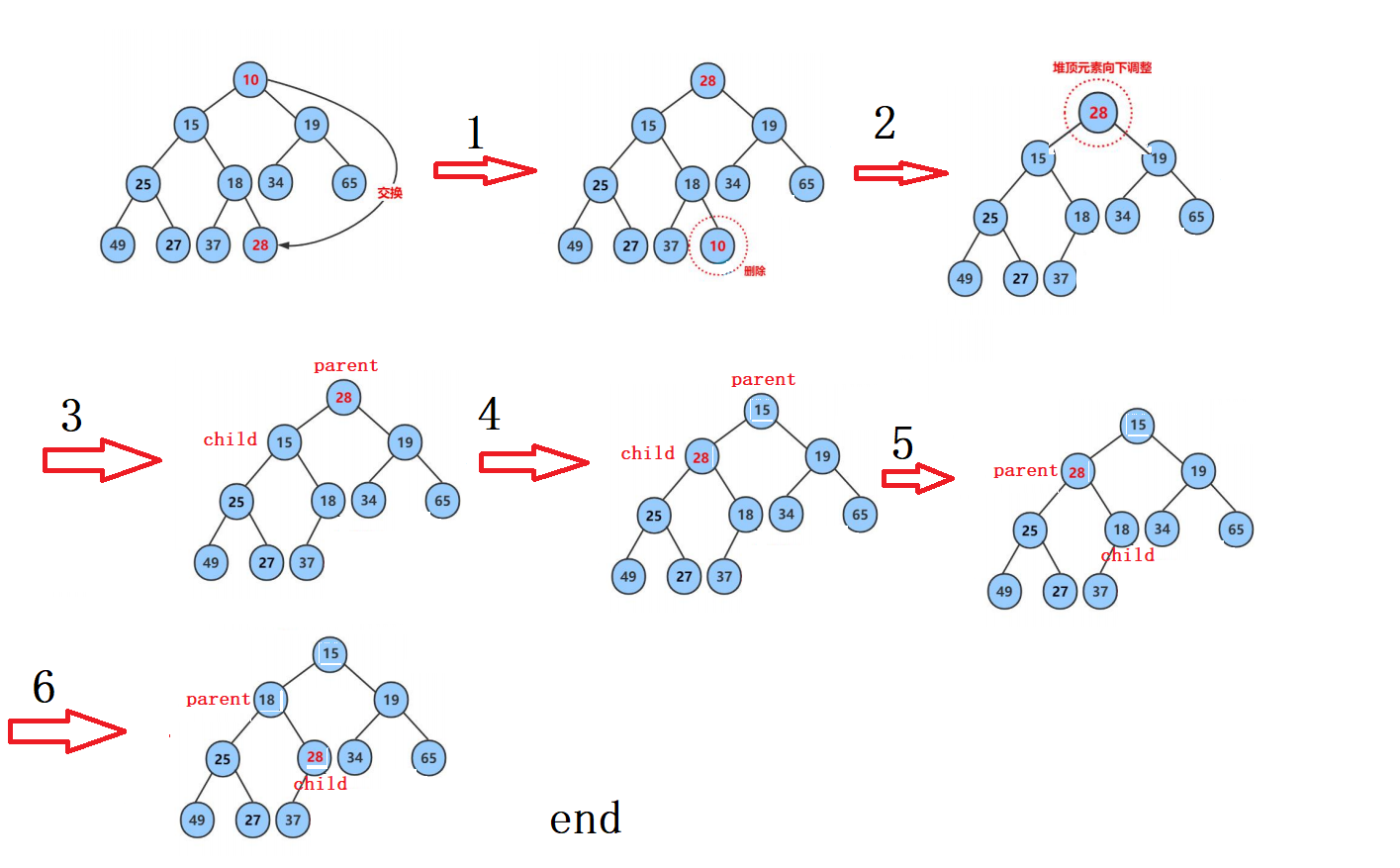
2、向下调整算法具体步骤(过程步骤如下图)：

a.我们将堆顶元素和数组最后一个元素交换后，此时堆顶的元素是数组的最后一个元素，我们要进行向下调整。定义parent为堆顶元素，查找2个子节点中较小的一个节点作为孩子节点。由于堆是数组结构实现，我们可以首先找到左孩子节点child = 2*parent+1。让左孩子和右孩子进行比较，较小的作为child的最后值。

b.如果孩子小于父亲，则交换，并继续往下调整。让parent到child的位置，再重新计算孩子。

c.当孩子大于等于元素总个数时，循环结束。因此循环的条件可以写为child<size.

注：循环过程中一旦成堆，则跳出循环。

功能实现:

void AdjustDown(HPDataType* a, size_t size, size_t root)
{
	size_t parent = root;
	size_t child = parent * 2 + 1;//先拿到左孩子
	while (child < size)
	{
		// 1、选出左右孩子中小的那个
		if (child + 1 < size && a[child + 1] < a[child])
		{
			++child;
		}
 
		// 2、如果孩子小于父亲，则交换，并继续往下调整
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}
void HeapPop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	Swap(&php->a[0], &php->a[php->size - 1]);
	--php->size;
	AdjustDown(php->a, php->size, 0);
}

3.6 判断是否为空 HeapEmpty

bool HeapEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}

3.7 求元素个数

size_t HeapSize(HP* php)
{
	assert(php);
	return php->size;
}

3.8 求堆顶元素

HPDataType HeapTop(HP* php)
{
	assert(php);
	assert(php->size > 0);
	return php->a[0];
}

 4.堆的应用：堆排序   ***

堆排序即利用堆的思想来进行排序，总共分为两个步骤：

1. 建堆

升序：建大堆

降序：建小堆

2. 利用堆删除思想来进行排序

建堆和堆删除中都用到了向下调整，因此掌握了向下调整，就可以完成堆排序。

 假设此时我们需要对数组元素进行升序排序，我们就可以使用我们刚刚实现的小堆。

4.1 堆排序实现过程分析

1、首先我们将数组的元素插入到堆中，根据向上调整，此时堆已经是小堆。

2、根据小堆的性质，堆顶的元素一定是该堆中最小的元素，因此我们取到堆顶的元素，再删除堆顶的元素让堆重新生成小堆。依次循环即可解决升序排序（降序排序只需将小堆改为大堆即可）。

4.2 堆排序实现代码

//堆排序
void HeapSort(int* a, int size)
{
	HP hp;
	HeapInit(&hp);
	for (int i = 0; i < size; ++i)
	{
		HeapPush(&hp, a[i]);
	}
	size_t j = 0;
	while (!HeapEmpty(&hp))
	{
		a[j] = HeapTop(&hp);
		j++;
		HeapPop(&hp);
	}
	HeapDestory(&hp);
}
int main()
{
	//	TestHeap();
 
	int a[] = { 4,2,1,3,5,7,9,8,6};
	HeapSort(a,sizeof(a)/sizeof(int));
	for (int i = 0; i < sizeof(a) / sizeof(int); ++i)
	{
		printf("%d ", a[i]);
	}
	
	return 0;
}

4.3 堆排序结果演示

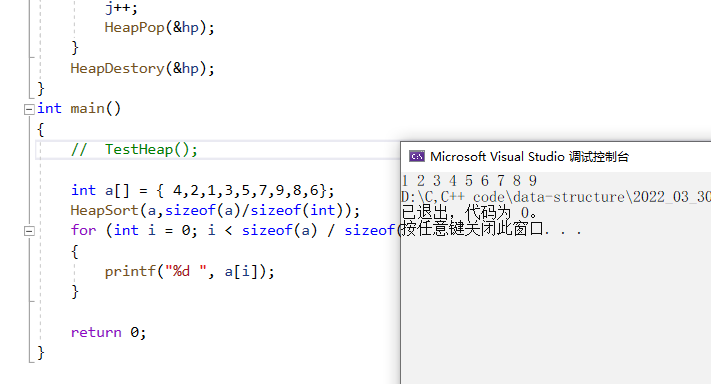
5.堆(小堆)的完整代码

2022_03_30 -- 堆/2022_03_30 -- 二叉树 · 李兴宇/数据结构 - 码云 - 开源中国 (gitee.com)

 (本篇完)