全新神经网络架构KAN——本文用于学习与探索_kan神经网络

论文地址：https://arxiv.org/pdf/2404.19756

Github：GitHub - KindXiaoming/pykan: Kolmogorov Arnold Networks

文档说明：Welcome to Kolmogorov Arnold Network (KAN) documentation! — Kolmogorov Arnold Network documentation

        本文仅用于论文学习、探讨以及应用探索，文中可能会出现理解上的错误与偏差，恳请各位看到后能够留言，我一定好好思考然后修改。

一、KAN的源头 / 思路来源 Kolmogorov-Arnold表示定理

1.1 理论概念

        KAN 网络结构的思路来自于Kolmogorov-Arnold表示定理，定理由由前苏联两位数学家Vladimir Arnold 和 Andrey Kolmogorov提出。

        定理指出，如何 f 是任意一个定义在有界域上的多变量连续函数，则函数 f 可以表示为有限数量的单变量、连续函数的两层嵌套加法的形式，即任何多变量连续函数都可以表示为单变量连续函数和加法运算的组合。       

 if f is a multivariate continuous function on a bounded domain, then f can be written as a finite composition of continuous functions of a single variable and the binary operation of addition

        该定理表明：真正的多元函数是一种求和，所有多元函数都可以表示为单变量函数求和的形式。从神经网络拟合任务函数(不同任务的函数维度不定，较为抽象)的角度看，这意味着对任一高维多变量函数的学习最终都可以被归约为对一组单变量函数的学习。

        补充1：Kolmogorov-Arnold定理和傅里叶级数很相似，傅里叶级数是一个连续的周期函数由谐波相关正弦函数的和生成。

        补充2：这个定理，只讲到‘两层叠加‘的结构，并没有讲到更深层次的叠加。

1.2 公式分析        

        论文中，对该定理和公式的表示如下，我们先来简单理解下（红色框由上到下）。

        第一个红框(多变量连续函数)：函数 f 的定义域是一个n维的闭区间[0, 1]的笛卡尔积，值域是实数集合R。简单来讲，函数 f 接受一个n维向量作为输入，并将其映射到实数集合R中的一个数。每个维度的取值范围都是[0, 1]，所以输入向量的每个分量都是在[0, 1]内取值的。

        第三个红框(两层嵌套函数)：Φq 是外部函数(outer functions)，Φq,p 是内部函数(inner functions)。对于内部函数，定义域是闭区间[0, 1]，值域是实数集合R；对于外部函数，定义域是实数集合R，值域也是实数集合R。

        第二个红框(完整函数表示)：直观看到函数 f，由两个嵌套的求和函数构成；外部函数Φq的参数是n个内部函数Φq,p的和！；整体来看 函数 f 是 (2n+1)个外部函数Φq的和。

二、对比MLP和KAN

        图1: KAN结构对标MLP，期望能作为比MLP更优的平替，因此先看一看MLP和KAN的对比。     

        KAN将可学习的激活函数放在了权重上，并且是可学习的激活函数（因此KAN训练困难、收敛慢），这些一维函数被参数化为B样条(基础样条, Basic Spline, B-Spline)。这意味着每个权重参数不再是一个单一的数值，而是一个函数（个人理解）

        MLP将固定的激活函数放置在节点，也就是神经元上；而可以学习的权重在边上，权重多以多维度的参数矩阵表现。

三、KAN网络结构 + 使用

3.1 思维链路

        1. 如何将 Kolmogorov-Arnold表示定理，应用、结合到现有深度学习任务中

        简单理解，思考一般的深度学习任务，每一个深度学习任务，尤其是端到端的任务，其实就是学习到一个函数 f ，使得 f(input) = truth。

        在深度学习中，我们使用神经网络拟合任务相关的多元函数 f，而根据Kolmogorov-Arnold表示定理，这个多元函数 f 又可以被单变量函数求和表示。因此，论文作者的想法是先找到Φq 、Φq,p这两个单变量函数，因此才挖掘、设计了KAN。

        理论上，只要两个KAN层（一个表示内部函数，一个学习外部函数）就能够表征在实数域的各类有监督学习任务。两个KAN层模拟了KA表示定理。

        补充：由于要学习的函数都是单变量函数，因此论文作者将每个1D的函数都参数化为Basic Spline(后面简化为B样条），具有局部B样条基函数的可学习系数，这一点对应本文章节二。

       2. KA定理和深度任务理论上可以结合，如何和现有的深层神经网络融合

        上述只是理论，两层的KAN还是太简单了，难以在实践中用光滑Spline近似or逼近任何函数，因此需要更多、更深层次的KAN网络。

        类比于现在的神经网络，当定义好了一层网络(由线性变换和非线性组成)后，就可以不断的叠加，使网络更深，学习到不同层级的特征表征等等......

        新的问题：在构建深层KAN之前，如何定义一个完整的KAN层？

        补充：2部分的内容，完全来自于原论文，基本原始翻译。

        3. 定义基础组件——KAN层

        论文中，将具有N(in)维输入和N(out)维输出的KAN层可以定义为1维函数的矩阵，公式如下：

        我的理解：一个KAN层可以表示为 [N(in)，N(out)]的一个矩阵，矩阵中的每个元素是一个1D、可学习、连续函数。

3.2 KAN网络推理细节（来自论文）

        假设现在有一个L+1层的KAN复合网络，每一层的节点数是[n0, n1, · · · , nL]；使用(l, j)表示第l层中的第j个神经元，使用x(l, j)表示这个神经元的值。

        再说第L层和第L+1层的联系，两层之间的神经元相互连接，共存在(nl * nl+1)个激活函数（前面讲过在KAN中每一个权重都是可学习的激活函数）。第 l 层中第 j 个神经元(l, j) 与 第 l+1 层中第 i个神经元(l + 1, i)，通过激活函数连接，激活函数表示为：Φ(l, i, j)

        补充：这里和传统神经网络很像，层之间全连接

        如果想进一步计算x(L+1, j)  ，通过如下式子（很好理解）：第L+1层的每一个神经元的值都由第L层的值构成（全连接），因为KAN将激活函数放置在了边上，所以来自第L层的值都会对应一个激活函数Φ(l, i, j) i = [0,1,2...,nl]，每个值经过对应的激活函数处理后，简单求和就得到了x(L+1, j)

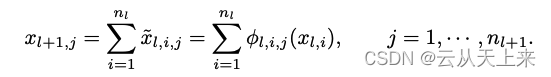
        总结：还是原来神经网络那套思想，层和层之间全连接，下一层的每一个元素都由上一层所有元素组合构成。区别在于(1) KAN将激活函数放在‘边’上，使得上一层每个元素都对应了一个激活函数。所有激活函数表现形式为矩阵，记为ΦL。

 3.3 KAN网络一般推理表达

        作者给出了一张基础两层KAN网络结构 

         如图，论文中展示的两层KAN网络（由下而上），第0层（最底层）表示内部函数，变量维度由n --> 2n + 1；第1层表示外部函数，变量维度由 2n + 1 --> 1，这个‘1’ 也就是多元函数的结果，是一个实数。

        将基础两层KAN网络推广到一般形式：图示见章节二开头图1(c)和(d)

        

3.4 KAN网络优化细节 

        1. 效仿残差网络结构，在激活函数中引入偏置函数b(x)

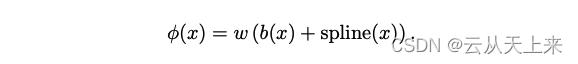
        其中偏置函数 b(x) 就是激活函数 silu(x) :

        而spline(x) 是一组一维函数的组合。

        注意：原论文中说到可训练参数w理论上是多余的，因为它可以融入到b(x) 和 spline(x)中，但是为了更好地控制激活函数功能，因此添加。个人猜测，大概率做个类似的对比实验。

        2. 初始化方式

        每个激活函数都被初始化为 。！这里不是很理解，具体看下图

        spline(x)的初始化，作者说的是将可训练参数通过绘制B样条曲线系数来实现，按照正太分布初始化，其中方差部分较小，通常设置为0.1（如果有读者对这个部分理解的更加深入，可以在评论区留言或者留下文章链接）

        可训练参数w，进行Xavier初始化。

        3. 更新样条曲线网格（暂时没懂，可能需要深度spline的原理）
        根据输入激活动态更新每个网格，以解决样条曲线定义在有界区域上，但激活值可以在训练过程中从固定区域演化出来的问题

四、优缺点分析

 4.1 优点

        1. 参与的运算可微，可以直接使用反向传播训练

        2. 在实际应用过程中，KAN可以可视化，提供MLP无法提供的可解释性和交互性。

        3. 拟合复杂函数，更准确

        4. KAN不会像MLP那样容易灾难性遗忘，缓解大模型的遗忘问题

4.2 缺点

        1. 维度灾难，以下结果来自GPT-3.5 + 个人理解，比较好理解

        在数学中，Spline / 样条是一种常用的插值方法，用于在给定的数据点之间生成平滑的曲线。然而，Spline样条在高维空间中存在维度灾难问题。

        维度灾难是指当数据的维度增加时，样本点之间的距离变得非常大，导致插值方法的效果变差。在Spline样条中，随着数据点的维度增加，需要更多的样本点来保持平滑性，否则曲线可能会出现过拟合的问题。

        具体来说，维度灾难问题在Spline样条中体现为以下几个方面：

        a. 数据点之间的距离增加：在高维空间中，数据点之间的距离会呈指数级增长。这意味着需要更多的样本点来捕捉数据的细节，否则插值的曲线可能会出现明显的偏差。

        b. 过拟合问题：由于维度灾难，Spline样条在高维空间中容易出现过拟合的问题。过拟合指的是模型过度适应训练数据，导致在新的数据上表现不佳。在Spline样条中，过拟合可能导致曲线在数据点之间出现剧烈的震荡，而不是平滑的曲线。（样条是一种特殊的函数，由多项式分段定义，如果目标是高维度曲线，那么在高维度空间进行拟合，样条每段之间可能会剧烈波动、震荡or曲折）

        c. 计算复杂度增加：随着数据维度的增加，计算Spline样条的复杂度也会增加。在高维空间中，需要更多的计算资源和时间来生成平滑的曲线。

       

        综上所述，Spline样条存在维度灾难问题，即在高维空间中插值效果变差、过拟合问题增加以及计算复杂度增加。为了解决这个问题，可以考虑降维技术或者使用其他更适合高维数据的插值方法。

        在论文中，提出了一种假设和证明，能够证明KAN的设计有机会解决维度灾难，貌似是从有限的推导中逼近真值。具体可看论文章节2.3中的Theorem 2.1 (Approximation theory, KAT)

        2. 深度KAN网络，缺少相关数学定理

        Kolmogorov-Arnold表示定理对应于两层的KANs。论文中说到，目前还没有一个“一般化”版本的定理对应于更深层次的KANs。

        文中表述的一般形式并没有相关支持。

        3. 实现技术上的缺陷

        (a) 学习的激活函数的成本比固定激活函数成本更高，表现为虽然参数很少，但是收敛的很慢

        (b) 论文作者是物理博士，因此对于训练和评估代码的优化不足

        (c) 貌似当前版本无法适配GPU，高效的实现是应用的第一步！

        (d) SGD、AdamW、Sophia等梯度下降算法是否能够找到KANs的局部最小值？存疑

五、笔者认为论文中比较重要or难以理解的部分

        论文章节2.3：Theorem 2.1 (Approximation theory, KAT)，逼近和证明的理论

        论文章节2.4：使spline grids更加精细化，以此来获得更加精准的函数逼近

        论文章节2.5.1：Sparsification ，将L1正则化 / L1稀疏化的概念引入，有两个修改。

                (1) KAN中不存在线性“权重”。线性权重被可学习的激活函数所取代，因此我们应该定义这些激活函数的L1范数

                (2) 我们发现L1不足以稀疏化KAN；相反，额外的熵正则化是必要的（细节见附录C）

        论文章节2.4：与MLP相比，‘神经缩放定律’ = 测试损失Loss随着模型参数的增加而减小的现象

        论文章节3：通过5个拟合函数的例子，证明KAN网络更加精准

参考资料1：号称能打败MLP的KAN到底行不行？数学核心原理全面解析_腾讯新闻

参考资料2:  激活函数-SwiGLU_silu激活函数-CSDN博客

参考资料3：KAN网络技术最全解析—最热KAN能否干掉MLP和Transformer？（收录于GPT-4/ChatGPT技术与产业分析）_kan模型-CSDN博客