PID控制算法基础介绍_pid控制算法中,哪一个参数能够减小系统的震荡(注释:震荡指无人机到达指定高度因为

PID控制的概念

生活中的一些小电器，比如恒温热水器、平衡车，无人机的飞行姿态和飞行速度控制，自动驾驶等等，都有应用到 PID——PID 控制在自动控制原理中是一套比较经典的算法。

为什么需要 PID 控制器呢？

你一定用过恒温热水壶，想让热水壶的水保持在一个恒定的温度，这时候就需要一种算法先将水温加热到目标位置附近，能够“预见”这个水温的变化趋势自动控制加热功率，然后还能根据各种环境影响因素去调节以维持设定目标。

PID算法：就是“比例（proportional）、积分（integral）、微分（derivative）”，是一种常见的“保持稳定”控制算法。

常见的PID控制系统框图：

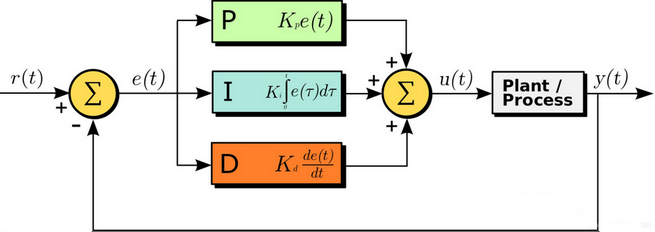
框图可以看出e(t)和u(t)的关系式：

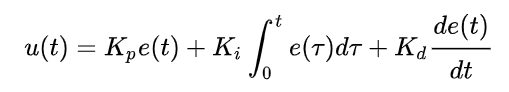
其中：
Kp：比例时间系数；
Ki：积分时间系数；
Kd：微分时间系数；
e：误差=设定值 - 回授值；
t：时间。

简单讲，根据给定值和实际输出值构成控制偏差，将偏差按比例、积分和微分通过线性组合构成控制量，对被控对象进行控制。

公式

PID原始公式：

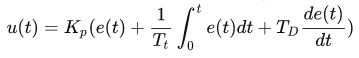
把Kp乘进去得：

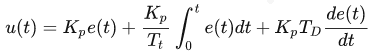
令


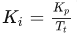
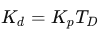
即可得到简化公式：

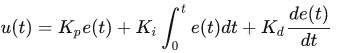
对于这个式子，其实涵盖了三种控制算法，每一种都可以单独拿出来。

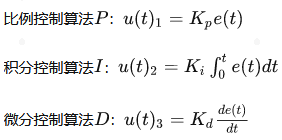
PID算法其实就是三个算法的组合，而且，在数学上面就是简单的代数和！

原理

1.比例控制算法

我们先说PID中最简单的比例控制，抛开其他两个不谈。假设我有一个水缸，最终的控制目的是要保证水缸里的水位永远的维持在1米的高度。假设初始时刻，水缸里的水位是0.2米，那么当前时刻的水位和目标水位之间是存在一个误差的error，且error为0.8。假设一个人通过往缸里加水的方式来控制水位。如果单纯的用比例控制算法，就是指加入的水量u和误差error是成正比的。即
u=kp*error
假设kp取0.5，
那么t=1时（表示第1次加水），u=0.5*0.8=0.4，所以这一次加入的水量会使水位在0.2的基础上上升0.4，达到0.6。
接着，t=2时刻（第2次加水），当前水位是0.6，所以error是0.4。u=0.5*0.4=0.2，会使水位再次上升0.2，达到0.8。
如此这么循环下去，就是比例控制算法的运行方法。
可以预见，最终水位会无限接近我们需要的1米。
但是，单单的比例控制存在着一些不足，其中一点就是：稳态误差。
像上述的例子，根据kp取值不同，系统最后都会达到1米，只不过kp大了到达的快，kp小了到达的慢一些。不会有稳态误差。但是，考虑另外一种情况，假设这个水缸在加水的过程中，存在漏水的情况，假设每次加水的过程，都会漏掉0.1米高度的水。仍然假设kp取0.5，那么会存在着某种情况，假设经过几次加水，水缸中的水位到0.8时，水位将不会再变换！！！因为，水位为0.8，则误差error=0.2。所以每次往水缸中加水的量为u=0.5*0.2=0.1。同时，每次加水，缸里又会流出去0.1米的水！！！加入的水和流出的水相抵消，水位将不再变化！！
也就是说，我的目标是1米，但是最后系统达到0.8米的水位就不再变化了，且系统已经达到稳定。由此产生的误差就是稳态误差了。

（在实际情况中，这种类似水缸漏水的情况往往更加常见，比如控制汽车运动，摩擦阻力就相当于是“漏水”，控制机械臂、无人机的飞行，各类阻力和消耗都可以理解为本例中的“漏水”）
所以，单独的比例控制，在很多时候并不能满足要求。

2.积分控制算法

接着说上面的例子，如果仅仅用比例，可以发现存在暂态误差，最后的水位就卡在0.8了。于是，在控制中，我们再引入一个分量，该分量和误差的积分是正比关系。所以，比例+积分控制算法为：
u=kp*error+ ki∗∫ error
还是用上面的例子来说明，第一次的误差error是0.8，第二次的误差是0.4，第三次的误差是0.2，至此，误差的积分（离散情况下积分其实就是做累加），∫error=0.8+0.4+0.2=1.4。先假设它积分系数为0.1，已知比例控制算法的输入和漏掉的相等，那么这时整个算法只需要看积分控制算法的输出就行了，故积分控制输出1.4*0.1=0.14，很显然，积分控制的加入打破了之前的稳定状态，之前会卡在0.8，现在至少会是0.8+0.14。（计算很随意，不要较真）这个时候的控制量，除了比例的那一部分，还有一部分就是一个系数ki乘以这个积分项。由于这个积分项会将前面若干次的误差进行累计，所以可以很好的消除稳态误差（假设在仅有比例项的情况下，系统卡在稳态误差了，即上例中的0.8，由于加入了积分项的存在，会让输入增大，从而使得水缸的水位可以大于0.8，渐渐到达目标的1.0。）这就是积分项的作用。另一方面积分项也加快了整体控制算法的响应速度。
（稳态误差又叫静差:被控量的稳定值和给定值之差，一般用于衡量系统的准确性）静差很难被消除，但是通过积分控制可以尽量去减小，而且积分系数不可太大，太大静差反而更大。

3.微分控制算法

换一个另外的例子，平稳的驾驶车辆，当发现前面有红灯时，为了使得行车平稳，基本上提前几十米就放松油门并踩刹车了。当车辆离停车线非常近的时候，则使劲踩刹车，使车辆停下来。整个过程可以看做一个加入微分的控制策略。
微分，说白了在离散情况下，就是error的差值，就是t时刻和t-1时刻error的差，即u=kd *(error(t)-error(t-1))，其中的kd是一个系数项。可以看到，在刹车过程中，因为error是越来越小的，所以这个微分控制项一定是负数，在控制中加入一个负数项，他存在的作用就是为了防止汽车由于刹车不及时而闯过了线。从常识上可以理解，越是靠近停车线，越是应该注意踩刹车，不能让车过线，所以这个微分项的作用，就可以理解为刹车，当车离停车线很近并且车速还很快时，这个微分项的绝对值（实际上是一个负数）就会很大，从而表示应该用力踩刹车才能让车停下来。
换到上面给水缸加水的例子，就是当发现水缸里的水快要接近1的时候，加入微分项，可以防止给水缸里的水加到超过1米的高度，说白了就是减少控制过程中的震荡。

从公式上看，微分控制算法如下：

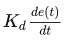
离散情况下，微分就是error的差值，就是当前时刻和上一时刻error的差，error指的是目标值和当前值的差值

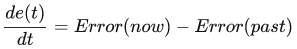
①当 当前值<目标值 时：一般在该调节过程中，误差是越来越小的(正实数运算)，这也就可以得

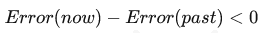
对于主要的比例控制而言，此时e(t)>0，二者符号相反，换言之，这里微分控制起到了削减比例控制力度的作用

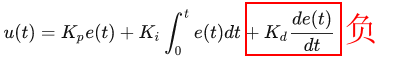
②当 当前值>目标值 时： 输出过大，需要减小，对于比例控制，e(t)<0，反观微分控制:

符号还是和比例控制相反

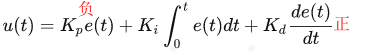
最终结论就是微分起到阻尼作用，减小震荡，提高稳定，减小变化趋势，但是也会降低响应速度。

通过下面的动图再直观看一下PID三个控制参数的影响：

从上面的动图可以看出：
1、Kp越大，越能快速接近目标值1.0
2、只调整Kp可能会存在稳定误差
3、加入Ki可以减小稳定误差，但同时也使得系统震荡加剧
4、加入Ki加快了整体的响应速度
5、加入Kd可以减小震荡，但也降低了响应速度(可以通过观察图像什么时间t首次碰到目标1.0)

思考

了解完上面的内容，需要对以下问题有一个答案：

1.为什么积分项可以消除稳态误差？

积分是什么？积分的几何意义概括的说是求曲边梯形的面积，将曲边梯形分成无数个小块，每块都可以近似拟合成长方形。将所有“长方形”的面积求和，即得到曲面梯形的面积。
所以积分的核心思想就是“求和”。
回顾一下积分项的公式：

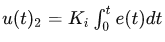
意思就是积分项输出，等于从第0时刻到当前这一时刻的偏差求和。那么，只要还存在偏差，积分项就一直有输出，直到偏差为0才停止，所以积分能减小或消除静差(稳态误差)。

2.为什么微分项可以抑制震荡、限制超调

我们再来回顾一下PID理论中微分项的公式：

Dout=Kp * Td * [ E(k)-E(k-1) ]/ T

公式核心部分是：[ E(k)-E(k-1) ]/ T， 即“本次偏差减去上次偏差，再除以两次间隔的时间”，这就是赤裸裸的求导啊！

求导是啥？就是求变化率呀！

所以，微分项输出就是由偏差变化率决定。即：偏差一旦有变化率，那微分项就有输出，否则偏差再大，只要变化率趋于0，那微分项就没输出。

那么结论就来了，只要我将微分项的输出量的符号设为负值。注意了，那么一旦系统有变化率，此时微分项输出多少，系统就得从总输出中减去多少。若前两次偏差的变化率非常大，那么本次总输出减去的值也就对应的非常多，也就是大大削弱了总输出量，这不相当于微分项作为一个阻尼，抑制了系统的输出吗？

更多内容查看：PID控制算法进阶

参考及扩展推荐：
https://blog.csdn.net/m0_38106923/article/details/109545445
https://zhuanlan.zhihu.com/p/32264695
https://www.zhihu.com/question/402289932
https://zhuanlan.zhihu.com/p/39573490
https://blog.csdn.net/kevinshift/article/details/124753170
https://www.woshipm.com/pd/4206858.html
https://zhuanlan.zhihu.com/p/85020348?utm_source=qq