devbox
AllinToyou
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

【图形图像的C++ 实现 01/20】 2D 和 3D 贝塞尔曲线_c++画三维曲线

作者：AllinToyou | 2024-02-21 15:25:05

赞

踩

c++画三维曲线

目录

一、说明

   以下文章介绍了用 C++ 计算和绘制的贝塞尔曲线（2D 和 3D）。
   贝塞尔曲线具有出色的数学能力来计算路径（从起点到目的地点的曲线）。曲线的形状由“控制点”决定。所讨论的曲线最重要的特征是平滑度。
   在许多应用和领域中，平滑度是不可或缺的。我们可以考虑机器人或其他机器的运动，其中运动必须是可预测的，以确保人员和硬件的安全（低磨损系数）。当机器人关节的轨迹被计算为平滑路径时，我们可以假设机器人将按照规划的路径平滑地移动，不会出现急动或意外移动。请注意，在我们考虑的机器人技术中，除了路径之外，还有速度、加速度、冲击力和电机扭矩。所有这些参数主要影响最终路径。
   除了机器人技术之外，贝塞尔曲线还用于动画、游戏和设计。

   为了绘图的目的，我将使用我之前的文章中讨论过的 C++ 的 matplotlib 库。
   头文件（用于绘图库）必须与您的 cpp 位于同一文件夹中。您的程序可以按如下方式编译，

​//compile
g++ my_prog.cpp -o my_prog -I/usr/include/python3.8 -lpython3.8// 
//run
./my_prog
//folder tree
├── my_prog
├── my_prog.cpp
├── matplotlibcpp.h

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8

​

二、贝塞尔曲线特征

   可以计算点集的贝塞尔曲线： { P0, P1, P2 …Pn}，其中n定义我们建模的曲线（多项式）的阶数。在每种情况下，第一个点和最后一个点定义曲线的起点和终点的位置。其他点 - 控制点通常不属于计算的曲线，而是影响贝塞尔曲线的形状。

   2D中的每个点P都有两个{x,y}笛卡尔坐标，但在3D中，点P按预期由三个{x, y, z}定义。

   贝塞尔曲线的显式定义可以指定如下（我们将在模拟中使用这个公式）。

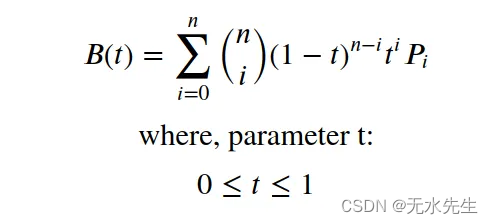
在这里插入图片描述
这里
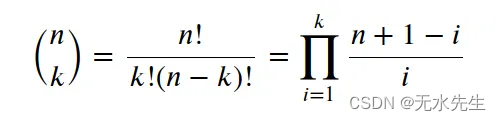
在这里插入图片描述

   是二项式系数。

   在我们的例子中，二项式系数的计算如下（如果您查看维基百科，您会发现递归实现，但这是最简单的版本或更直观）。

   C++ 中的实现可以如下所示，

​double computeBinominal(int n, int k)
{
    double value = 1.0;
    for (int i = 1; i <= k; i++)
    {
        value = value * ((n + 1 - i) / i);
    }
    if (n == k){
        value = 1;
    }
    return value;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12

​
平面空间中的四个点P 0 、P 1 、P 2 和P 3 定义三次贝塞尔曲线。该曲线可以建模为三阶多项式。
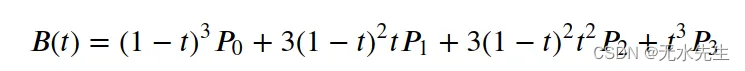
在这里插入图片描述

当提供六个点P 0、P 1、P 2、P 3、P4和P5时，贝塞尔曲线被计算为五阶多项式。

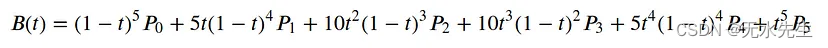
在这里插入图片描述

三、模拟

   现在我们将显示上面定义的曲线的 2D 和 3D 模拟（针对 4 点和 6 点）。下面的代码为您提供了计算和绘制您想要的任何数字点P 的贝塞尔曲线的绝佳机会。

x{2.5, 1.5, 6.0, 10.0}; 
y{0.5, 5.0, 5.0, 0.5};

x{2.5, 1.5, 6.0, 10.0}; 
//与 2D y{0.5, 5.0, 5.0, 0.5}相同；
//与 2D z{1.0, 2.0, 3.0, 4.0}相同；

X{2.5, 1.5, 6, 10, 7, 3}; 
Y{0.5, 5.0, 5.0, 0.5, 1.0, 2.0};

X{2.5, 1.5, 6.0, 10.0, 7.0, 3.0}; // 对于 2D 
Y{0.5, 5.0, 5.0, 0.5, 1.0 , 2.0}; // 对于 2D 
Z{1.0, 2.0, 3.0, 4.0, 5.0, 0.1};

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13

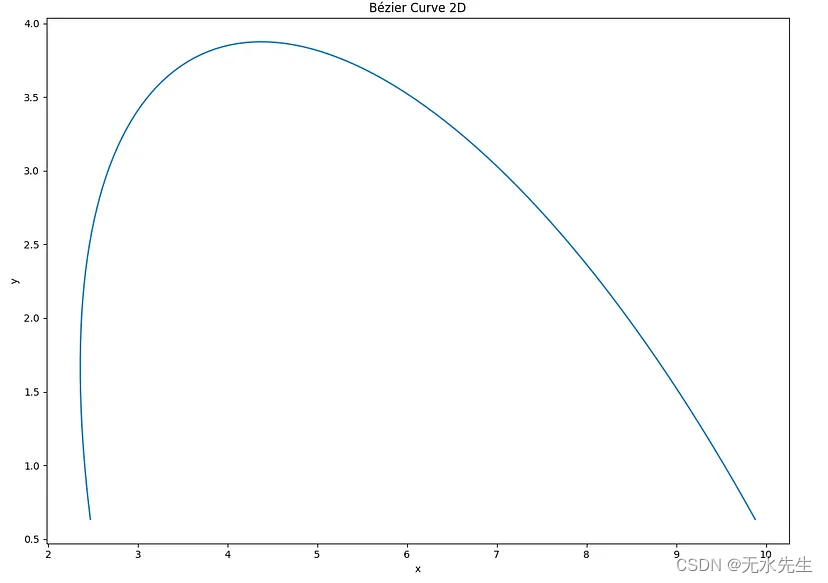
在这里插入图片描述
对于相同阶的多项式（三阶），我们可以计算 3D 贝塞尔曲线。

x{2.5, 1.5, 6.0, 10.0}; //same as 2D
y{0.5, 5.0, 5.0, 0.5}; //same as 2D
z{1.0, 2.0, 3.0, 4.0};

  • 1
  • 2
  • 3

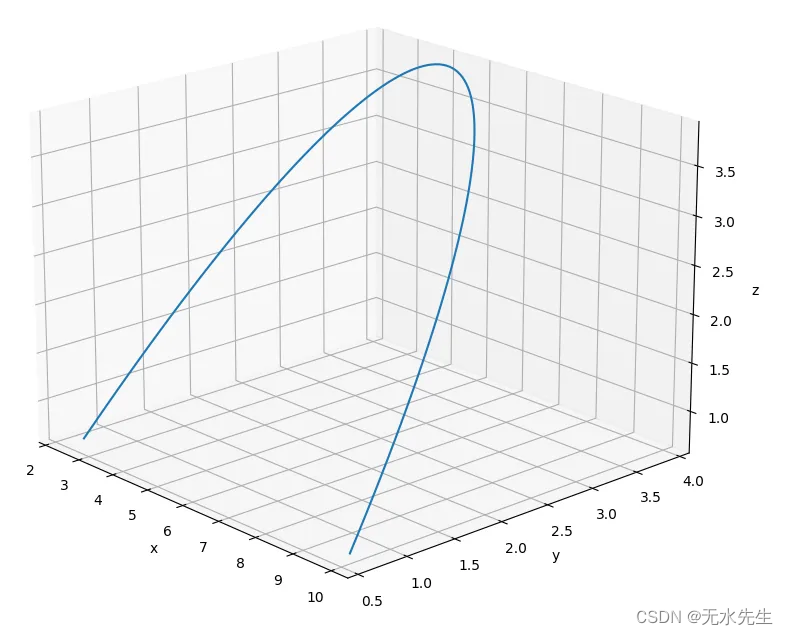
在这里插入图片描述
这是一条 2D 贝塞尔曲线，它是针对五阶多项式（六点）计算的。

X{2.5, 1.5, 6, 10, 7, 3};
Y{0.5, 5.0, 5.0, 0.5, 1.0 , 2.0};

  • 1
  • 2

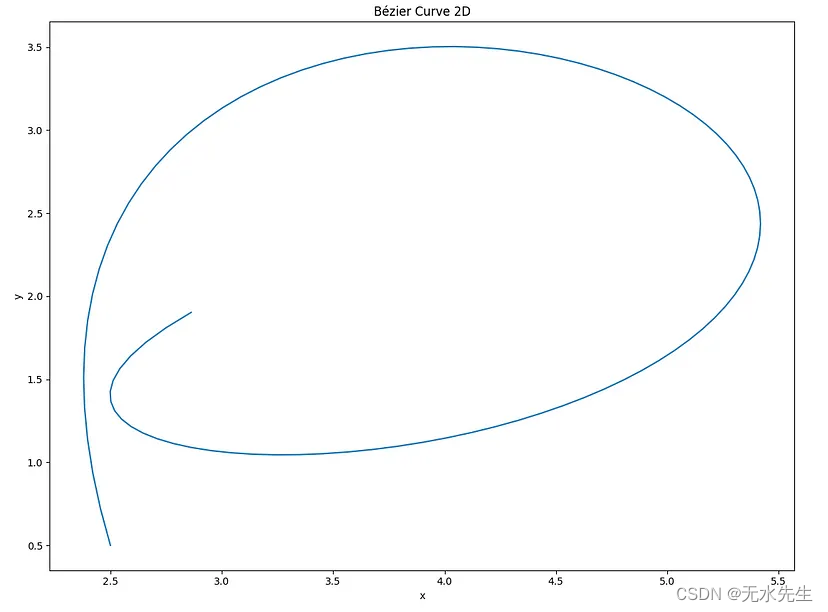
在这里插入图片描述
和以前一样，我们可以绘制 3D 贝塞尔曲线。

X{2.5, 1.5, 6.0, 10.0, 7.0, 3.0}; //as for 2D
Y{0.5, 5.0, 5.0, 0.5, 1.0 , 2.0}; //as for 2D
Z{1.0, 2.0, 3.0, 4.0, 5.0, 0.1};

  • 1
  • 2
  • 3

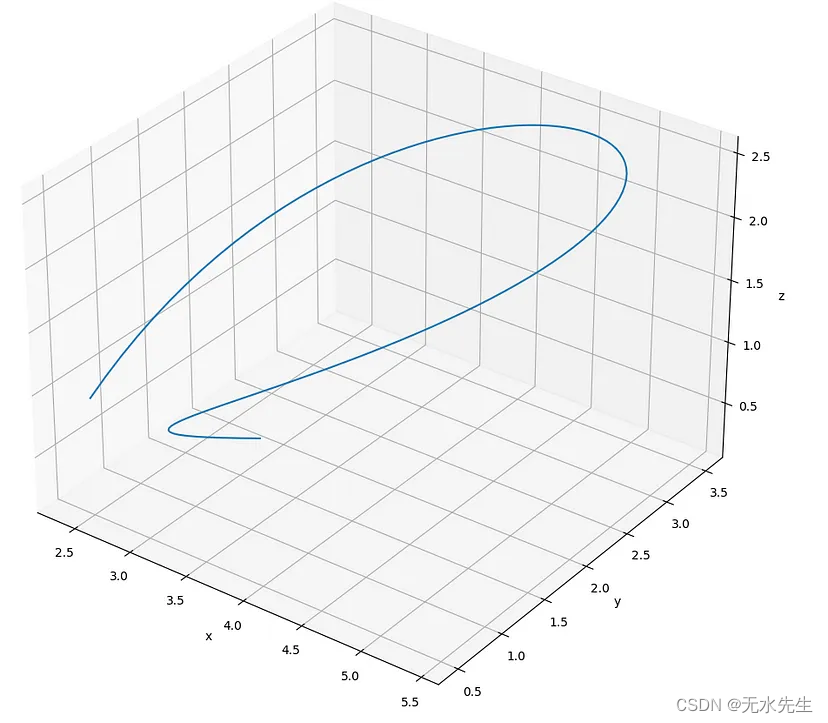
在这里插入图片描述

四、全部代码如下

/// g++ bezier_curve.cpp -o t -I/usr/include/python3.8 -lpython3.8

#include <iostream>
#include <vector>
#include <tuple>
#include <math.h>

#include "matplotlibcpp.h"

namespace plt = matplotlibcpp;

//-----------------------------------------------------------

std::tuple<std::vector<double>, std::vector<double>> computeBesierCurve2D(std::vector<double> xX, std::vector<double> yY)
{

    std::vector<double> bCurveX;
    std::vector<double> bCurveY;
    double bCurveXt;
    double bCurveYt;

    for (double t = 0.01; t <= 1; t += 0.01)
    {

        bCurveXt = std::pow((1 - t), 3) * xX[0] + 3 * std::pow((1 - t), 2) * t * xX[1] + 3 * std::pow((1 - t), 1) * std::pow(t, 2) * xX[2] + std::pow(t, 3) * xX[3];
        bCurveYt = std::pow((1 - t), 3) * yY[0] + 3 * std::pow((1 - t), 2) * t * yY[1] + 3 * std::pow((1 - t), 1) * std::pow(t, 2) * yY[2] + std::pow(t, 3) * yY[3];

        bCurveX.push_back(bCurveXt);
        bCurveY.push_back(bCurveYt);
    }

    return std::make_tuple(bCurveX, bCurveY);
}

//-----------------------------------------------------------

void plot2D(std::tuple<std::vector<double>, std::vector<double>> data)
{

    std::vector<double> xX = std::get<0>(data);
    std::vector<double> yY = std::get<1>(data);


    plt::plot(xX, yY);
    plt::show();
}

//-----------------------------------------------------------

std::tuple<std::vector<double>, std::vector<double>, std::vector<double>> computeBesierCurve3D(std::vector<double> xX, std::vector<double> yY, std::vector<double> zZ)
{

    std::vector<double> bCurveX;
    std::vector<double> bCurveY;
    std::vector<double> bCurveZ;
    double bCurveXt;
    double bCurveYt;
    double bCurveZt;

    for (double t = 0.01; t <= 1; t += 0.01)
    {

        bCurveXt = std::pow((1 - t), 3) * xX[0] + 3 * std::pow((1 - t), 2) * t * xX[1] + 3 * std::pow((1 - t), 1) * std::pow(t, 2) * xX[2] + std::pow(t, 3) * xX[3];
        bCurveYt = std::pow((1 - t), 3) * yY[0] + 3 * std::pow((1 - t), 2) * t * yY[1] + 3 * std::pow((1 - t), 1) * std::pow(t, 2) * yY[2] + std::pow(t, 3) * yY[3];
        bCurveZt = std::pow((1 - t), 3) * yY[0] + 3 * std::pow((1 - t), 2) * t * yY[1] + 3 * std::pow((1 - t), 1) * std::pow(t, 2) * yY[2] + std::pow(t, 3) * yY[3];

        bCurveX.push_back(bCurveXt);
        bCurveY.push_back(bCurveYt);
        bCurveZ.push_back(bCurveZt);
    }

    return std::make_tuple(bCurveX, bCurveY, bCurveZ);
}

//-----------------------------------------------------------

void plot3Dexample()
{

    std::vector<double> xX;
    std::vector<double> yY;
    std::vector<double> zZ;
    double theta;
    double r;
    double z_inc = 4.0 / 99.0;
    double theta_inc = (8.0 * M_PI) / 99.0;

    for (double i = 0; i < 100; i += 1)
    {
        theta = -4.0 * M_PI + theta_inc * i;
        zZ.push_back(-2.0 + z_inc * i);
        r = zZ[i] * zZ[i] + 1;
        xX.push_back(r * std::sin(theta));
        yY.push_back(r * std::cos(theta));
    }

    plt::plot3(xX, yY, zZ);
    plt::show();
}

//-----------------------------------------------------------

void plot3D(std::tuple<std::vector<double>, std::vector<double>, std::vector<double>> data)
{

    std::vector<double> xX = std::get<0>(data);
    std::vector<double> yY = std::get<1>(data);
    std::vector<double> zZ = std::get<2>(data);

    plt::plot3(xX, yY, zZ);
    plt::xlabel("x");
    plt::ylabel("y");
    plt::set_zlabel("z");
    plt::show();
}

//-----------------------------------------------------------

double computeBinominal(int n, int k)
{

    double value = 1.0;

    for (int i = 1; i <= k; i++)
    {

        value = value * ((n + 1 - i) / i);
    }

    if (n == k){
        value = 1;
    }
    
    return value;
}

//-----------------------------------------------------------

std::tuple<std::vector<double>, std::vector<double>> computeNVertexBasierCurve2D(std::vector<double> xX, std::vector<double> yY)
{

    std::vector<double> bCurveX;
    std::vector<double> bCurveY;

    int n = xX.size() - 1;
    std::cout << "n :" << n << "\n";

    for (double t = 0.0; t <= 1.0; t += 0.01)
    {

        double bCurveXt{0};
        double bCurveYt{0};

        for (int i = 0; i <= n; ++i)
        {

            bCurveXt += computeBinominal(n, i) * std::pow((1 - t), (n - i)) * std::pow(t, i) * xX[i];
            bCurveYt += computeBinominal(n, i) * std::pow((1 - t), (n - i)) * std::pow(t, i) * yY[i];
            //std::cout << " t= "<< t<< " i=" << i << " bCurveXt=" << bCurveXt << " = " << computeBinominal(n, i)  << " * " << std::pow((1 - t), (n - i))  << " * " << std::pow(t, i) << " * " << xX[i] << std::endl;
        }

        bCurveX.push_back(bCurveXt);
        bCurveY.push_back(bCurveYt);
    }

    return std::make_tuple(bCurveX, bCurveY);
}

std::tuple<std::vector<double>, std::vector<double>, std::vector<double>> computeNVertexBasierCurve3D(std::vector<double> xX, std::vector<double> yY, std::vector<double> zZ)
{

    std::vector<double> bCurveX;
    std::vector<double> bCurveY;
    std::vector<double> bCurveZ;

    int n = xX.size() - 1;
    std::cout << "n :" << n << "\n";

    for (double t = 0.0; t <= 1.0; t += 0.01)
    {

        double bCurveXt{0};
        double bCurveYt{0};
        double bCurveZt{0};

        for (int i = 0; i <= n; ++i)
        {

            bCurveXt += computeBinominal(n, i) * std::pow((1 - t), (n - i)) * std::pow(t, i) * xX[i];
            bCurveYt += computeBinominal(n, i) * std::pow((1 - t), (n - i)) * std::pow(t, i) * yY[i];
            bCurveZt += computeBinominal(n, i) * std::pow((1 - t), (n - i)) * std::pow(t, i) * zZ[i];
            //std::cout << " t= "<< t<< " i=" << i << " bCurveXt=" << bCurveXt << " = " << computeBinominal(n, i)  << " * " << std::pow((1 - t), (n - i))  << " * " << std::pow(t, i) << " * " << xX[i] << std::endl;
        }

        bCurveX.push_back(bCurveXt);
        bCurveY.push_back(bCurveYt);
        bCurveZ.push_back(bCurveZt);
    }

    return std::make_tuple(bCurveX, bCurveY, bCurveZ);
}


//-----------------------------------------------------------

int main()
{

    std::vector<double> xX{2.5, 1.5, 6, 10};
    std::vector<double> yY{0.5, 5, 5, 0.5};
    std::vector<double> zZ{1.0, 2.0, 3.0, 4.0};

    std::tuple<std::vector<double>, std::vector<double>> bCurve2D = computeBesierCurve2D(xX, yY);
    plot2D(bCurve2D);
    
    std::tuple<std::vector<double>, std::vector<double>, std::vector<double>> bCurve3D = computeBesierCurve3D(xX, yY, zZ);
    plot3D(bCurve3D);
    
    std::vector<double> xXn{2.5, 1.5, 6, 10, 7, 3};
    std::vector<double> yYn{0.5, 5, 5, 0.5, 1.0 , 2.0};
    std::vector<double> zZn{1, 2, 3, 4, 5, 0.1};

    std::tuple<std::vector<double>, std::vector<double>> bCurve2DxN = computeNVertexBasierCurve2D(xXn, yYn);
    plot2D(bCurve2DxN);
    
    std::tuple<std::vector<double>, std::vector<double>, std::vector<double>> bCurve3DxN = computeNVertexBasierCurve3D(xXn, yYn, zZn);
    plot3D(bCurve3DxN);

}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102
  • 103
  • 104
  • 105
  • 106
  • 107
  • 108
  • 109
  • 110
  • 111
  • 112
  • 113
  • 114
  • 115
  • 116
  • 117
  • 118
  • 119
  • 120
  • 121
  • 122
  • 123
  • 124
  • 125
  • 126
  • 127
  • 128
  • 129
  • 130
  • 131
  • 132
  • 133
  • 134
  • 135
  • 136
  • 137
  • 138
  • 139
  • 140
  • 141
  • 142
  • 143
  • 144
  • 145
  • 146
  • 147
  • 148
  • 149
  • 150
  • 151
  • 152
  • 153
  • 154
  • 155
  • 156
  • 157
  • 158
  • 159
  • 160
  • 161
  • 162
  • 163
  • 164
  • 165
  • 166
  • 167
  • 168
  • 169
  • 170
  • 171
  • 172
  • 173
  • 174
  • 175
  • 176
  • 177
  • 178
  • 179
  • 180
  • 181
  • 182
  • 183
  • 184
  • 185
  • 186
  • 187
  • 188
  • 189
  • 190
  • 191
  • 192
  • 193
  • 194
  • 195
  • 196
  • 197
  • 198
  • 199
  • 200
  • 201
  • 202
  • 203
  • 204
  • 205
  • 206
  • 207
  • 208
  • 209
  • 210
  • 211
  • 212
  • 213
  • 214
  • 215
  • 216
  • 217
  • 218
  • 219
  • 220
  • 221
  • 222
  • 223
  • 224
  • 225
  • 226
  • 227
  • 228
  • 229

​五、资源和下载

下面给出源代码资源下载链接地址：
https://download.csdn.net/download/gongdiwudu/88821722

​

​

​​

​

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/AllinToyou/article/detail/124696
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号