1. Abstract
本文旨在简单介绍下各种轻量级网络,纳尼?!好吧,不限于轻量级
2. Introduction
2.1 Inception
在最初的版本 Inception/GoogleNet,其核心思想是利用多尺寸卷积核去观察输入数据。举个栗子,我们看某个景象由于远近不同,同一个物体的大小也会有所不同,那么不同尺度的卷积核观察的特征就会有这样的效果。于是就有了如下的网络结构图:

图1: Inception module, naive version
于是我们的网络就变胖了,通过增加网络的宽度,提高了对于不同尺度的适应程度。但这样的话,计算量有点大了。
2.2 Pointwise Conv
为了减少在上面结构的参数量并降低计算量,于是在 Inception V1 的基础版本上加上了 1x1 卷积核,这就形成了 Inception V1 的最终网络结构,如 Figure 2。
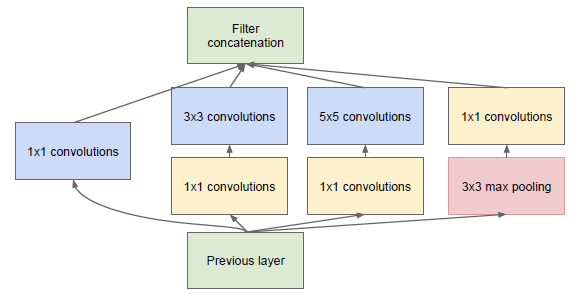
图2: Inception module with dimension reductions
这个 1x1 卷积就是 Pointwise Convolution,简称 PW。利用它的目的主要是为了减少维度,还用于引入更多的非线性。
我们来简单计算下:假定上一层输出的 feature map 维度为 100x100x128,经过256个大小为 5x5 的卷积后,输出的 feature map 大小为 100x100x256。这里卷积参数为 $256*5*5*128=819,200$。而假如上一层的输出先经过 32 个大小为 1x1 的卷积后,再经过256个大小为 5x5 的卷积,那么输出维度保持不变的情况下,卷积参数减少为 $128*1*1*32\ +\ 32*5*5*256=204,800$,降低为原来的 $\frac{204800}{819200}=\frac{1}{4}$。
PW 主要用于数据降维,减少参数量。也有使用 PW 做升维的,在 MobileNet v2 中就使用 PW 将 feature map 的宽度扩张了6倍,丰富输入数据的特征。
2.3 Kernel Replace
Inception V2 和 V3 版本为了进一步降低卷积参数采用小卷积来替换大卷积,同 VGG 套路。
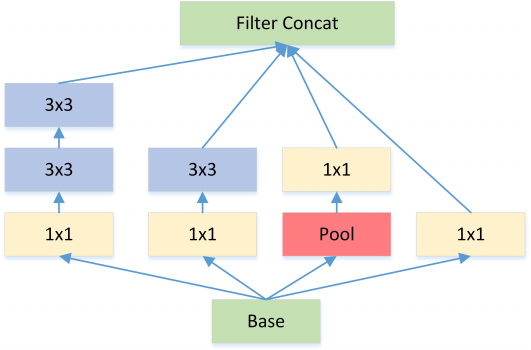
图3: Each 5×5 convolution is replaced by two 3×3 convolution
大尺寸的卷积核可以带来更大的感受野,但也意味着会产生更多的参数,比如 5x5 卷积核的参数有 25 个,3x3 卷积核的参数有 9 个,前者是后者的 25/9=2.78 倍。因此,GoogLeNet 团队提出可以用 2 个连续的 3x3 卷积层组成的小网络来代替单个的 5x5 卷积层,即在保持感受野范围的同时又减少了参数量。除了规整的的正方形,还有分解版本的 3x3 = 3x1 + 1x3,这个效果在深度较深的情况下比规整的卷积核更好(feature map 大小建议在 12 到 20 之间)。
2.4 Feature Map Downsample
一般情况下,如果想让图像缩小,可以有如下两种方式:
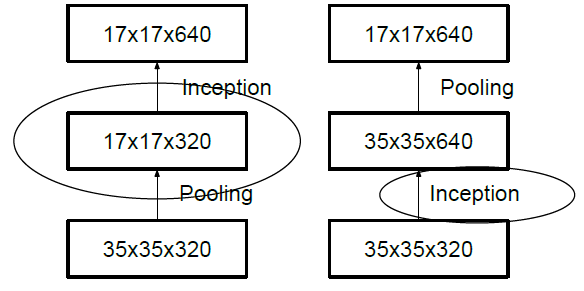
先 pooling 再作 Inception 卷积,或者先作 Inception 卷积再作 Pooling。前者先作 Pooling 会导致特征缺失遇到 bottleneck,后者则相对来说计算量更大。为了同时保持特征表示且降低计算量,将网络结构改为 Figure 5,使用两个并行化的模块来降低计算量(卷积、池化并行执行,再进行合并)。
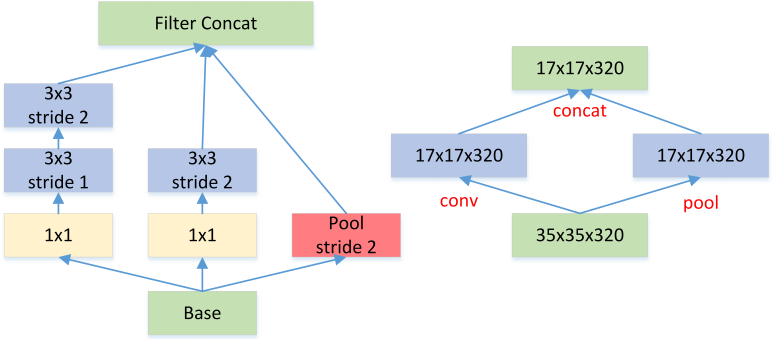
图5: Feature map Downsample
2.5 Bottleneck
Bottleneck 三步走:先 PW 对数据进行降维,再进行常规卷积,最后 PW 对数据进行升维,形如沙漏。
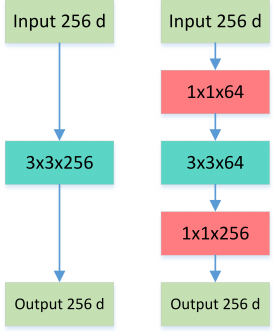
图6: Normal VS Bottleneck
这就是所谓的 Bottleneck 结构,上图中后者的计算量 $256*1*1*64 + 64*3*3*64 + 64*1*1*256 = 69,632$ 远小于前者 $256*3*3*256 = 589,824$。
2.6 Inception + ResNet

图7: Residual VS Residual+Inception
2.7 Group Conv Depthwise Separable Conv
Group Convolution 分组卷积,最早见于AlexNet,当时受限于硬件,Group Convolution被用来切分网络,使其在2个GPU上并行运行。
让我们先来回顾下常规卷积,具体可参考这篇博文。对于输入为 $I$x$H$x$W$ 大小的 Input Features,经过 $O$ 个 $K$x$K$x$I$ 大小的卷积核后,输出 Output Features 的通道数也是 $O$。这里的卷积参数量为 $O*K*K*I$,输入和输出 map 的连接方式如下图左所示,输出的每个通道都和输入的所有通道相关联:
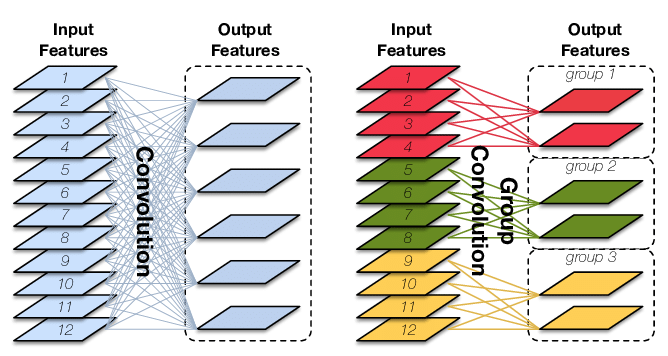
图8: Standard convolution (left) and group convolution(right). The latter enforces a sparsity pattern by partitioning theinputs (and outputs) into three disjoint groups
Group Conv 顾名思义,则是对输入 feature map 进行分组,然后每组分别卷积。假设输入 feature map 的尺寸仍为 $I$x$H$x$W$,输出 Output Features 的通道数也是 $O$,如果设定要分成 $G$ 个 groups,则每组的输入 feature map 数量为 $\frac{I}{G}$,每组的输出 feature map 的数量为 $\frac{O}{G}$,每个卷积核的尺寸为 $K$x$K$x$\frac{I}{G}$,每组的卷积核数量为 $\frac{N}{G}$,卷积核的总数仍为 $O$ 个,卷积核只与其同组的输入 map 进行卷积,卷积核的总参数量为 $O*K*K*\frac{I}{G}$,可见,总参数量减少为原来的 $\frac{1}{G}$,其连接方式如上图右所示,group1 输出 map 数为 2,有 2 个卷积核,每个卷积核的 channel 数为 4,与 group1 的输入 map 的 channel 数相同,卷积核只与同组的输入 map 卷积,而不与其他组的输入 map 卷积。
Group Conv 的用途包括:
- 减少参数数量,分成 $G$ 组,则该层的参数量减少为原来的 $\frac{1}{G}$。
- Group Conv 可以看成是一种 {\color{red}structured sparse},每个卷积核的尺寸由 $K$x$K$x$I$ 变成了 $K$x$K$x$\frac{I}{G}$,这里可以将其余的 ($I$-$\frac{I}{G}$x$K$x$K$) 维的参数视为 0。实际中,Group Conv 在减少参数量的同时有可能获得更好的效果(相当于{\color{red}正则})。
Depthwise Convolution 其实是 Group Conv 的一种特例,简称 DW。当分组数量等于输入 map 数量,输出 map 数量也等于输入 map 数量,即 $G=O=I$,$O$ 个卷积核每个尺寸为 $K$x$K$x$1$ 时,Group Convolution 就成了Depthwise Convolution。Depthwise Separable Convolution 则是DW+PW 的组合体,如Figure 9,参见 Xception 等,参数量进一步缩减。

图9: Depthwise Separable Convolution
更进一步,如果分组数 $G=O=I$,同时卷积核的尺寸与输入 map 的尺寸相同,即 $K=H=W$,则输出 map 为 $I$x$1$x$1$ 即长度为 $O$ 的向量,此时称之为 Global Depthwise Convolution (GDC),见 MobileFaceNet,可以看成是全局加权池化,与 Global Average Pooling (GAP) 的不同之处在于,GDC 给每个位置赋予了可学习的权重(对于已对齐的图像这很有效,比如人脸,中心位置和边界位置的权重自然应该不同),而 GAP 每个位置的权重相同,全局取个平均,如下图所示:
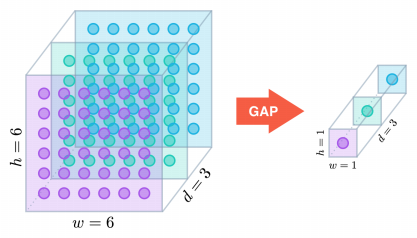
图10: Global Depthwise Convolution
2.8 Summary
- 多个不同尺寸的卷积核,提高对不同尺度特征的提取。
- PW 卷积,降维或升维的同时,提高网络的表达能力。
- 多个小尺寸卷积核替代大卷积核,加深网络的同时减少参数量。
- Bottleneck 结构,大大减少网络参数量。
- DW 设计,再度减少参数量。
3. SqueezeNet
4. ResNet ResNeXt Res2Net
4.1 ResNet
关键字: identity mappings, shortcut connections
ResNet 算的上是最具有影响力的网络结构之一了。
4.1.1 The Challenges with Deeper Networks
引用 cs231n 网络规模的建议:
The takeaway is that you should not be using smaller networks because you are afraid of overfitting. Instead, you should use as big of a neural network as your computational budget allows, and use other regularization techniques to control overfitting
实际上,一个明显的设计趋势是网络变得更深(使网络变得更宽不是首选,因为容易过拟合)。然而在实践中,当深度不断加深时,我们会看到一些异常现象 -- 通过增加普通网络的深度,训练和测试误差实际上比对应的浅层网络差。众所周知,如果未正确初始化权重,增加深度会导致梯度爆炸或消失。但是,这可以通过 batch normalization 等技术来抵消。尽管如此,更深的网络会出现收敛性下降 - 准确性变得饱和,误差仍然高于浅层网络。
4.1.2 Intuition behind Residual Networks
Make it deep, but remain shallow
给定一个 shallower network,怎样才能添加额外的层使其更深,同时又不降低准确性呢?这是一个棘手的问题,但有一种见解是,如果添加到网络的额外层是个 identity mappings,它们将变得等同于 shallower network,这可能不会产生更高的训练误差。
Understanding residual
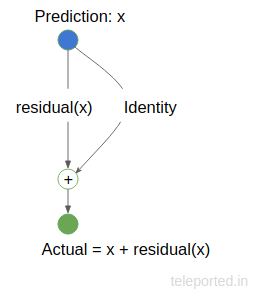
图11: A residual is the error in a result.
上图中,$X$ 是我们的预测值,我们希望它等于 Actual. 但是,如果我们的预测存在偏差,我们的残差函数 residual() 就会启动来纠正我们的 Prediction 以匹配 Actual. 而如果 X==Actual, residual(X) 将为 0, Identity 就只是复制了 X.
4.1.3 The Residual Network
将上述二者结合起来就是我们的 Residual Network 了,他是通过 shortcut connections 实现的。
Shortcut connections are those skipping one or more layers. In our case, the shortcut connections simply perform identity mapping, and their outputs are added to the outputs of the stacked layers. Identity shortcut connections add neither extra parameter nor computational complexity. The entire network can still be trained end-to-end by SGD with backpropagation, and can be easily implemented using common libraries without modifying the solvers.
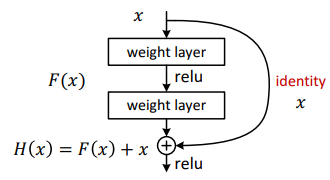
图12: The reusable residual network.
网络在数学上描述为:
Figure13 展示了一个 34 层的 ResNet arch。 Kaiming He在他的一个演讲中对ResNet和Inception模型(GoogLeNet)进行了比较,这是迄今为止的另一种最先进的架构。据他介绍,Inception模型的特点是有3个属性。
- Bottleneck - reducing dimensions before applying expensive operations
- Multiple Branches - extracting features of various sizes by using multiple and different filters parallelly
- Shortcuts - as used in ResNet - to go deep
ResNet有两个上述属性,缺少 Multiple Branches,后续 ResNeXt 将针对这一问题进行改进。
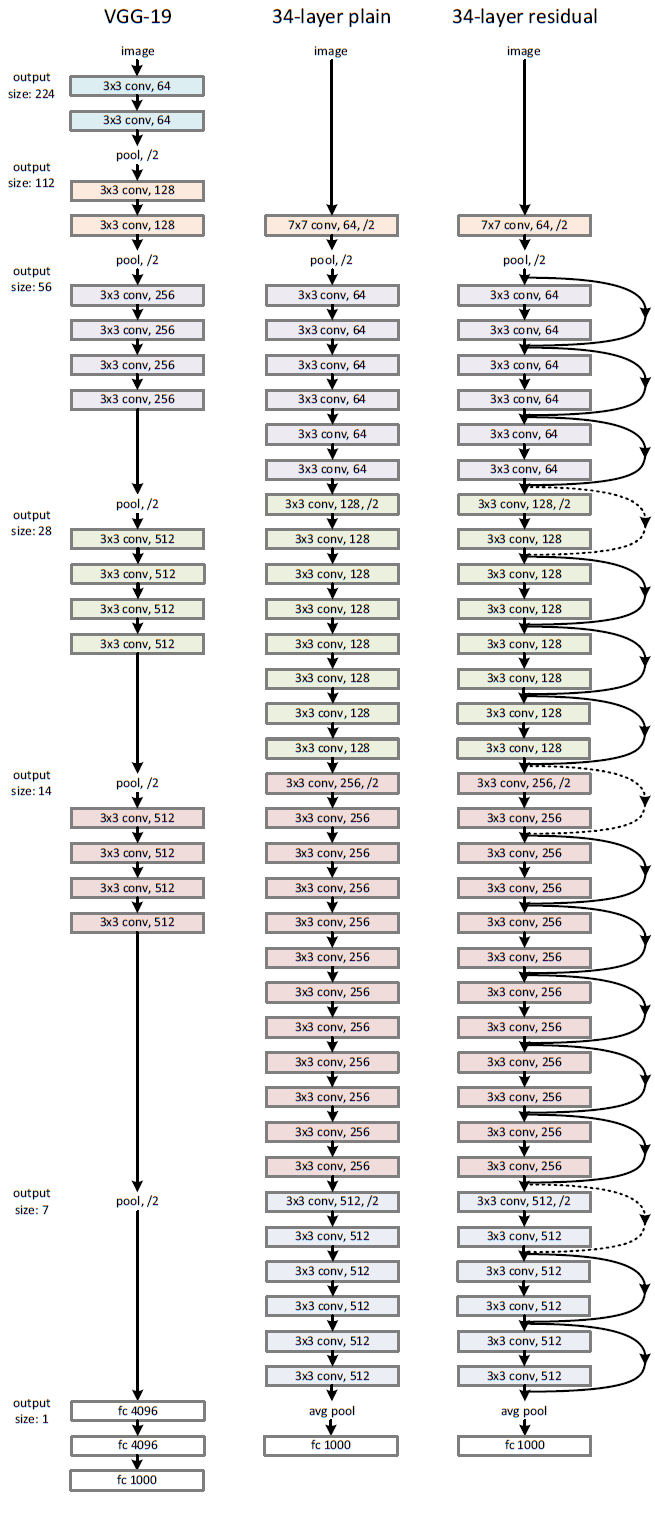
图13: A 34 layer ResNet with VGG 19 side by side
4.2 ResNeXt
关键字:stacking, split-transform-merge, cardinality
ResNeXt 这篇文章看到最后你会发现,原来就是 ResNet + Group Conv 的组合罢了。但是,和 Xception 论文套路一样,作者是经过一步步理论证明了的。
论文一开始采用 VGG stacking 的思想和 Inception 的 split-transform-merge 思想,这里有一个超参数 cardinality (the size of the set of transformations),如图所示:
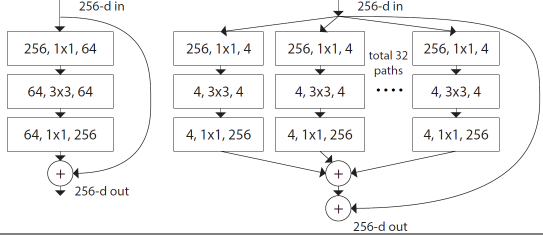
图14: Left: A block of ResNet. Right: A block of ResNeXt with cardinality = 32, with roughly the same complexity. A layer is shown as (# in channels, filter size, # out channels).
论文中表示增加 cardinality 比增加网络的深度和宽度更有效。随后作者展示了三种相同的 ResNeXt blocks: Figure 15(a) 被称为 aggregated residual transformations。Figure 15(b) 采用了两层卷积后 concatenate,再卷积,有点类似 Inception-ResNet,只不过这里的 paths 都是相同的拓扑结构。Figure 15(c) 采用的是 grouped convolutions,这个 group 参数就是 caffe 的 convolusion 层的 group,最后把 channels 合并。作者在文中明确说明这三种结构是严格等价的,并且用这三个结构做出来的结果一模一样,在论文中展示的是 Figure 15(c) 的结果,因为 Figure 15(c) 的结构比较简洁而且速度更快。
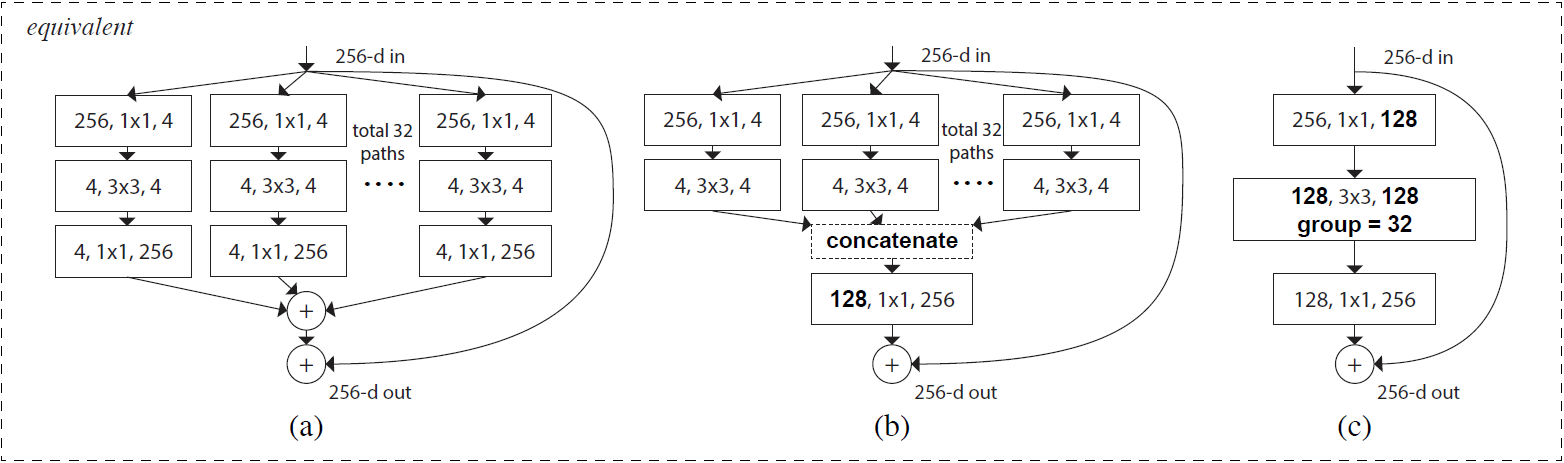
图15: Equivalent building blocks of ResNeXt. (a): Aggregated residual transformations, the same as Fig. 1 right. (b): A block equivalent to (a), implemented as early concatenation. (c): A block equivalent to (a,b), implemented as grouped convolutions [24].
Notations in bold text highlight the reformulation changes. A layer is denoted as (# input channels, filter size, # output channels).
实验中,为了控制网络参数量,作者利用 $C$(cardinality) 和 $d$(width of bottleneck) 两个超参数来进行平衡(ResNeXt50_32Cx4d$\approx$ResNet50),这里面 $width\ of\ bottleneck * cardinality = width\ of\ group\ conv$.
4.2Res2Net
关键字:multi-scale, groups, residual-like connections
Res2Net 这篇文章水不水暂时还不好说。
视觉领域中,多尺度特征是很重要的:
- objects may appear with different sizes in a single image.
- essential contextual information of an object may occupy a much larger area than the object itself.
- perceiving information from different scales is essential for understanding parts as well as objects for tasks such as finegrained classification and semantic segmentation.
如 Figure 16 所示,本文设计了一致更精细的 block, 拥有 multi-scale featue:
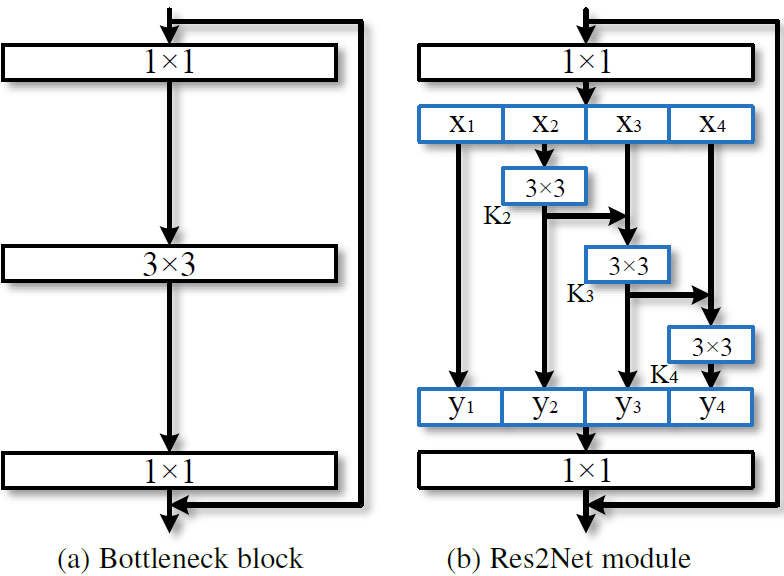
图16: Comparison between the bottleneck block and the proposed Res2Net module (the scale dimension s = 4).
这里,将普通的 3x3xn conv 换成了$s$ 个 3x3xw conv。然后将这些 groups 按照 residual-like style 进行连接,从而提高输出特征的尺度。具体的,考虑到计算量,第一个 group 没有经过卷积而直接输出了;同时,第一个 group 也没有送给第二个 group 输入作 Eltwise。最后,每组输出的 feature map 通过 concat 操作送入 1x1 的 PW 用于进行特征融合。我们知道,每经过一个 3x3 conv 操作,特征的感受野就随之变大。
这里引入一个新的维度 $s$(scale) 来表示整体 group 的数量,scale 同 depth, width, cardinality 相似,都为基本量。本文实验发现,通过增加scale的数量的提升效果要比其他量要好。这里先事先说下,不要将 scale 同 cardinality 进行等价,因为后面在每个 group 的基础上又引入了 cardinality 操作。。。
如 Figure17 所示,Res2Net block 还可以嵌入 cardinality 和 SE 模块:
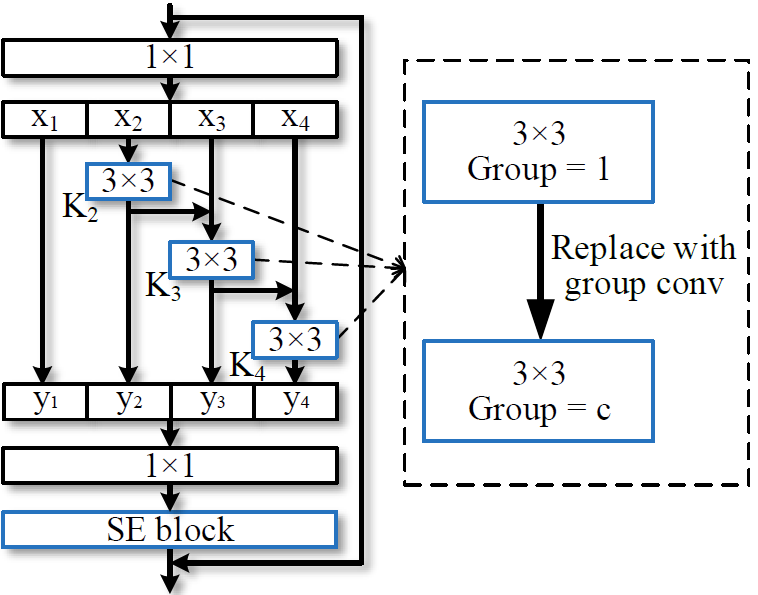
图17: The Res2Net module can be integrated with the dimension cardinality(ResNeXt, replace conv with group conv) and SE blocks.
源码 由 PyTorch 实现
5. DenseNet DPN
6. SENet GENet SKNet GCNet
6.1 SENet
这里就简单把官方对于 SENet 的解析搬过来了,同时作者提供了源码链接,Caffe 实现。
Convolution
A convolutional filter is expected to be an informatiive combination
• Fusing channel-wise and spatial information
• Within local receptive fields
图18: Normal Convolution.
我们从最基本的卷积操作开始说起。近些年来,卷积神经网络在很多领域上都取得了巨大的突破。而卷积核作为卷积神经网络的核心,通常被看作是在局部感受野上,将空间上(spatial) 的信息和通道上(channel-wise) 的信息进行聚合的信息聚合体}。卷积神经网络由一系列卷积层、非线性层和下采样层构成,这样它们能够从全局感受野上去捕获图像的特征来进行图像的描述。
Exploration on Spatial Enhancement
然而去学习一个性能非常强劲的网络是相当困难的,其难点来自于很多方面。有很多工作被提出来从空间维度层面来提升网络的性能,如 Inception 结构中嵌入了多尺度信息,聚合了多种不同大小的感受野的特征来获得性能增益;在 Inside-outside Network 中考虑了空间中的上下文信息;还有将 Attention 机制引入到空间维度上等等。这些工作都获得了相当不错的成果。
Squeeze-and-Excitation (SE) Networks
If a network can be enhanced from the aspect of channel relationship?
• Motivation
– Explicitly model channel-interdependencies within modules
– Feature recalibration
* Selectively enhance useful features and suppress less useful ones
已经有很多工作在空间维度上来提升网络的性能。那么很自然想到,网络是否可以从其他层面来考虑去提升性能,比如考虑特征通道之间的关系?我们的工作就是基于这一点并提出了 SENet,在我们提出的结构中,Squeeze 和 Excitation 是两个非常关键的操作,所以我们以此来命名。我们的动机是希望显式地建模特征通道之间的相互依赖关系。另外,我们并不打算引入一个新的空间维度来进行特征通道间的融合,而是采用了一种全新的“特征重标定”策略。具体来说,就是通过学习的方式来自动获取到每个特征通道的重要程度,然后依照这个重要程度去提升有用的特征并抑制对当前任务用处不大的特征。
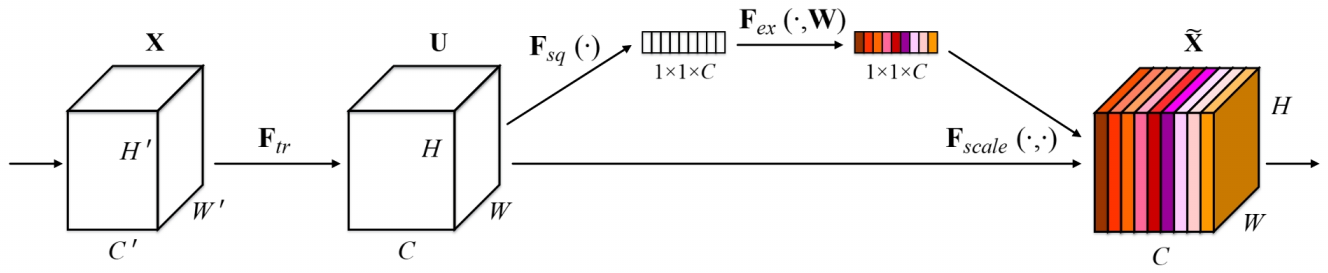
图20: A Squeeze-and-Excitation block
上图是我们提出的 SE 模块的示意图。给定一个输入 $X$, 其特征通道数为 $C^{'}$,通过一系列卷积等一般变换后得到一个特征通道数为 $C$ 的特征 $U$,接下来我们将通过三个操作来重标定前面的到特征 $U$。
首先是 Squeeze 操作,我们顺着空间维度来进行特征压缩,将每个二维的特征通道变成一个实数,这个实数某种程度上具有全局的感受野,并且输出的维度和输入的特征通道数相匹配。它表征着在特征通道上响应的全局分布,而且使得靠近输入的层也可以获得全局的感受野,这一点在很多任务中都是非常有用的。
其次是 Excitation 操作,它是一个类似于循环神经网络中门的机制。通过参数 $W$ 来为每个特征通道生成权重,其中参数 $W$ 被学习用来显式地建模特征通道间的相关性。
最后是一个 Reweight 的操作,我们将 Excitation 的输出的权重看做是进过特征选择后的每个特征通道的重要性,然后通过乘法逐通道加权到先前的特征上,完成在通道维度上的对原始特征的重标定
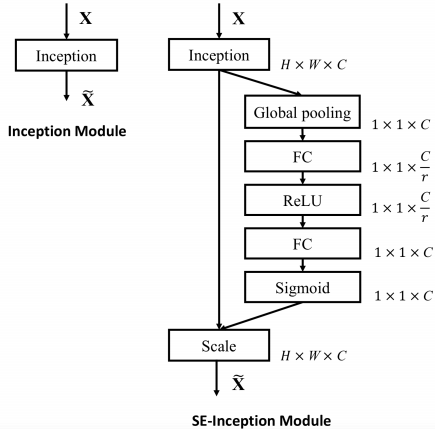 | 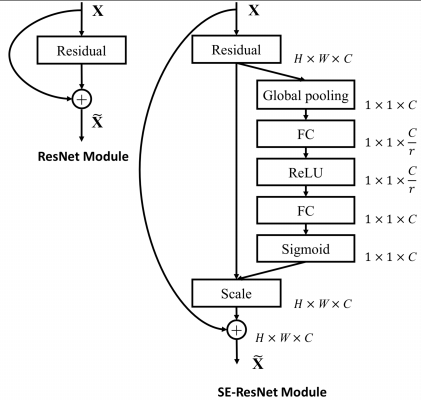 |
上左图是将 SE 模块嵌入到 Inception 结构的一个示例。方框旁边的维度信息代表该层的输出。这里我们使用 global average pooling 作为 Squeeze 操作。紧接着两个 Fully Connected 层组成一个 Bottleneck 结构去建模通道间的相关性,并输出和输入特征同样数目的权重。我们首先将特征维度降低到输入的 1/16,然后经过 ReLu 激活后再通过一个 Fully Connected 层升回到原来的维度。这样做比直接用一个 Fully Connected 层的好处在于:1)具有更多的非线性,可以更好地拟合通道间复杂的相关性;2)极大地减少了参数量和计算量。然后通过一个 Sigmoid 的门获得 $0 \sim 1$ 之间归一化的权重,最后通过一个 Scale 的操作来将归一化后的权重加权到每个通道的特征上。
除此之外,SE 模块还可以嵌入到含有 skip-connections 的模块中。上右图是将 SE 嵌入到 ResNet 模块中的一个例子,操作过程基本和 SE-Inception 一样,只不过是在 Addition 前对分支上 Residual 的特征进行了特征重标定。如果对 Addition 后主支上的特征进行重标定,由于在主干上存在 $0 \sim 1$ 的 scale 操作,在网络较深 BP 优化时就会在靠近输入层容易出现梯度消散的情况,导致模型难以优化。
目前大多数的主流网络都是基于这两种类似的单元通过 repeat 方式叠加来构造的。由此可见,SE 模块可以嵌入到现在几乎所有的网络结构中。通过在原始网络结构的 building block 单元中嵌入 SE 模块,我们可以获得不同种类的 SENet。
论文中还讨论了一些训练策略、耗时和性能分析,这里就不详细描述了。总体来说就是 SENet 结构实现简单,在耗时增加较低的情况下可以作用于不同的 building block 单元中并提升性能。
6.2 GENet
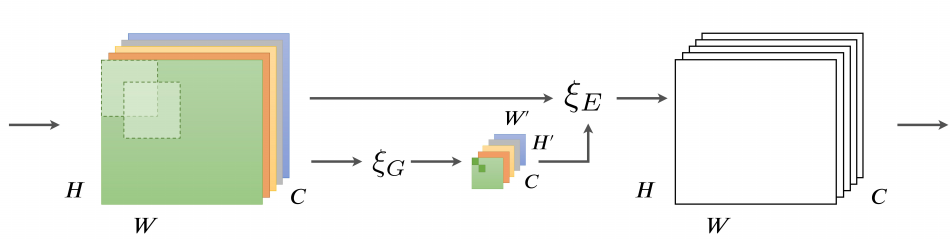
GENet 这篇文章则是从空间角度出发,首先利用 Gather Operator 操作,将输入的 feature map $x$ 利用卷积或者池化操作降维得到 $\tilde{x}$; 然后执行 Excite Operator 操作:使用 Nearest Neighbor Interpolation 操作将其 resize 到和 $x$ 相同 shape,最后经过 sigmoid 后和 $x$ 做点积运算 $x \odot{f(\tilde{x})}$。
对于 Gather Operator 操作,论文中实验表明,使用 Global Average Pooling 或者 Global Conv 时结果最好。。。和 SENet 一样。。。
其他细节和具体 caffe 实现和 prototxt 参考源码。
6.3 SKNet
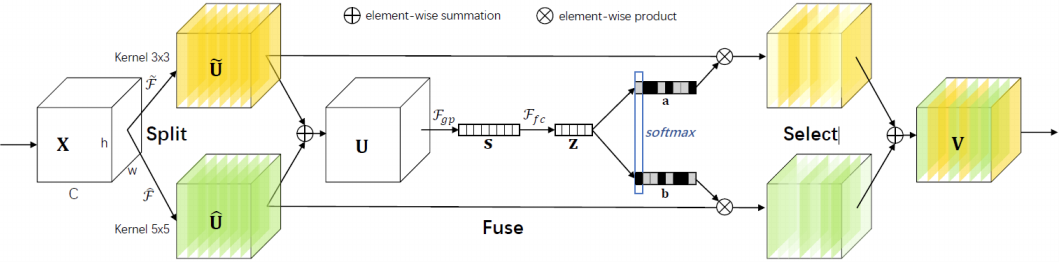
图24: Selective Kernel Convolution.
SKNet 可以算是 SENet 的递进版本了,这个网络主要分为 Split,Fuse,Select 三个操作。
Split 操作是指对特征向量 X 进行不同卷积核大小的卷积操作(包括 efficient group/depthwise conv, BN, ReLU,不同卷积核大小可考虑使用空洞卷积)得到输出 $\widehat{U}$ 和 $\widetilde{U}$。
Fuse: 先进行Eltwise $U=\hat{U} + \tilde{U}$, $F_{gp}$ 为全局平均池化操作,$F_{fc}$ 是先降维再升维的两层全连接层(实际上可以用 PW 卷积实现),需要注意的是输出的两个矩阵 $a$ 和 $b$,其中矩阵 $b$ 为冗余矩阵,在如图两个分支的情况下 $b=1-a$ (具体操作为先经过 Softmax 层,再经过 Slice)。
Select 操作对应于 SE 模块中的 Scale, 区别是 Select 使用 $a$ 和 $b$ 两个权重矩阵对 $\widetilde{U}$ 和 $\widehat{U}$ 进行加权操作,然后求和得到最终的输出向量 $V$。
具体细节参考 源码链接。
6.4 GCNet
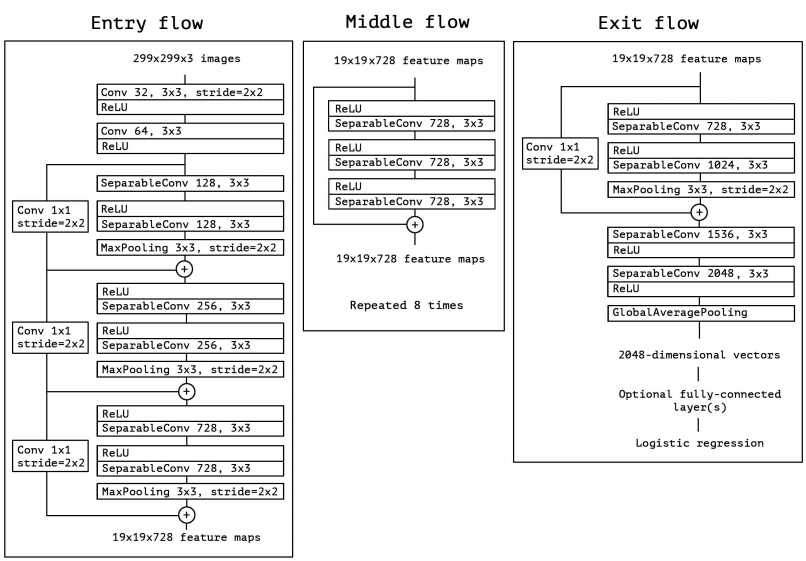
7. Xception
Xception 实际上就是从另一个角度来思考 Inception 的网络结构,同时在 Inception 的基础上将 Depthwise Separable Conv 发扬光大了!
7.1. The Inception Hypothesis
初始的 Inception V1 结构考虑从多尺度卷积核角度来观察输入数据的特征,Inception V3 则是从参数量和计算量角度来尝试改进。但我们也可以把 Inception V3 结构理解为:通过显式地将操作分解为一系列独立的通道相关性和空间相关性的学习,从而使得学习的过程变得更加简单和高效。具体来说,Inception V1 里各个卷积核需要同时学习空间上的相关性和通道间的相关性,结合了 spatial dimensions 和 channels dimensions;而 Inception V3 结构,先通过一组 1x1 PW 卷积来学习通道相关性,将输入数据映射到多个单独的小空间(降维了),然后对于所有这些小空间,通过常规的 3×3 卷积,5×5 卷积等来学习空间相关性。因此,Inception 结构背后的基本假设是,通道相关性和空间相关性之间的耦合性已经充分分离,这样的话最好不要将它们联合起来学习。于是便有了 Xception:将通道相关性和空间相关性分开学习的结构设计。
7.2. Extreme Inception
在 Inception 中,特征可以通过 1×1 卷积,3×3 卷积,5×5 卷积,pooling 等进行提取,Inception 结构将特征类型的选择留给网络自己训练,也就是将一个输入同时输给几种提取特征方式,然后做 concat 。Inception-v3的结构图如下:
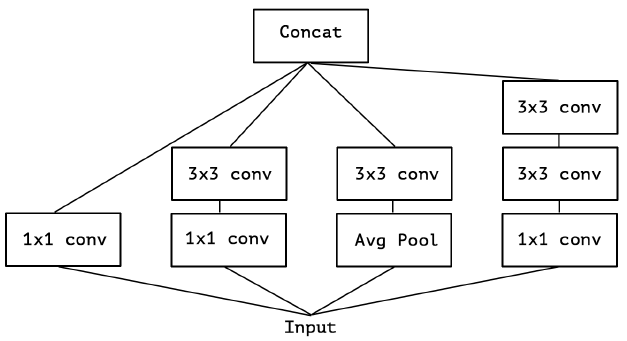
对 Inception-v3 进行简化,去除 Inception-v3 中的 avg pool 后,输入的下一步操作就都是 1×1 PW 卷积了:
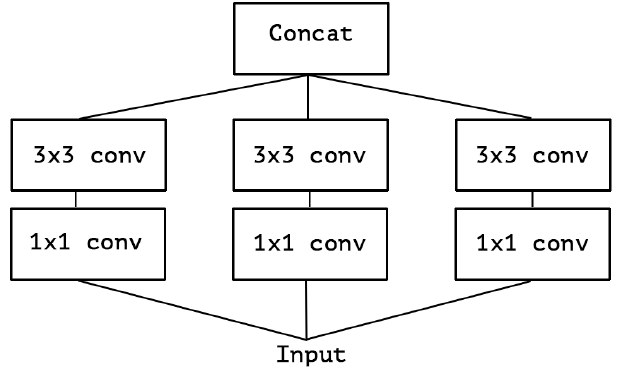
再进一步假设,3 个 PW 卷积核统一起来变成共用一个 PW 卷积,后面的三个 3x3 卷积核则分别”负责“一部分通道(Group Conv):
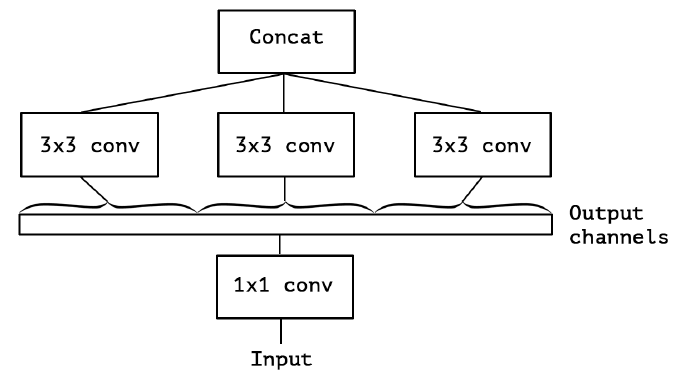
最后 Extreme Inception 闪亮登场,对 PW 卷积后的每个channel分别进行 3×3 卷积操作(Depthwise Conv, DW}),最后将结果 concat:
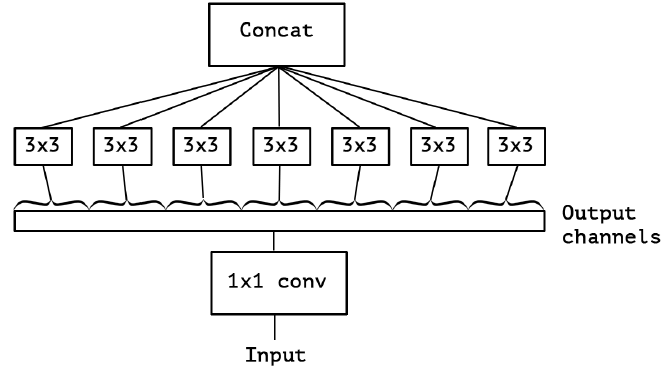
作者发现,在 Extreme Inception 模块中,用于学习空间相关性的 3×3 的 DW 卷积,和用于学习通道间相关性的 1×1 PW 卷积之间,不使用非线性激活函数时,收敛过程更快、准确率更高。
7.3. Xception
Xception 常用版本是将 DW 和 PW 交换了个位置:Extreme Inception 先进行 1×1 PW 卷积,再进行 3×3 DW 卷积;Depthwise Separable Conv 先进行 3×3 DW卷积,再进行 1×1 PW 卷积(作者认为这个差异并没有大的影响)。
理论上计算量相比:
其中 $I$ 为输入通道数,$O$ 是输出通道数,$K$ 是标准卷积核大小。我们可以看到,当我们使用 3x3 卷积核的时候,参数量约等于标准卷积核的 $\frac{1}{9}$,大大减少参数量,从而加快训练速度。具体网络结构图如 Figure 29:
8. MobileNet
8.1 MobileNet V1
MobileNet V1 理解起来就是对 Depthwise Separable Convolution 的加强使用。
结构上同 Xception 的区别在于,这里每个卷积之后都有 BN + ReLU 单元,如 Figure 30 所示。
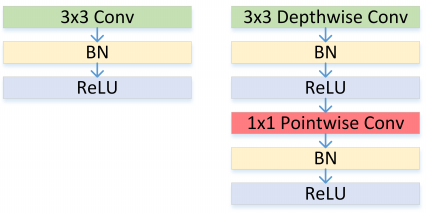
图30: Left: Standard convolutional layer with batchnorm and ReLU. Right: Depthwise Separable convolutions with Depthwise and Pointwise layers followed by batchnorm and ReLU.
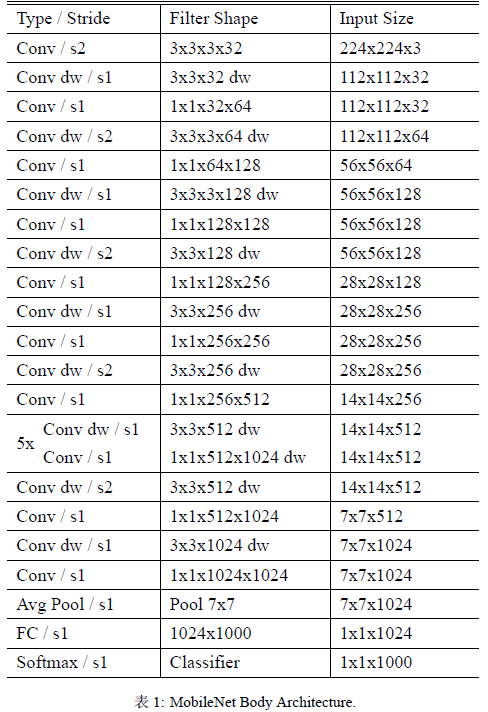
不考虑最后用来分类的全连接层,网络一共有 {\color{red}28} 层(DW 和 PW 单独作为一层来统计),具体见 Table 1。
由于 DW 的计算量较低,因此几乎所有($95\%$ of the computation time and $75\%$ of the parameters)的计算量都集中于密集的 1×1 PW 里。特别的,与训练大型模型相反,这里使用较少的正则化和数据增强技术,因为小型模型的过拟合问题较少。训练策略基本上同 Inception V3,但作者建议较少甚至不使用 weight decay (l2 regularization) 在 DW 中,因为这个层的参数本来就很少了。
文中引入了两个超参数 $\alpha$ 和 $\rho$。
-
$\alpha$ 是个 width multiplier, 目的是降低 feature map 的宽度(channel)以减少计算复杂度和参数数量(大概$\alpha^2$)的作用,其取值范围为 $(0,1]$, 其中 $\alpha=1$ 代表 baseline MobileNet。Table 2 对比了 width multiplier $\alpha$ 大小对网络性能的影响:
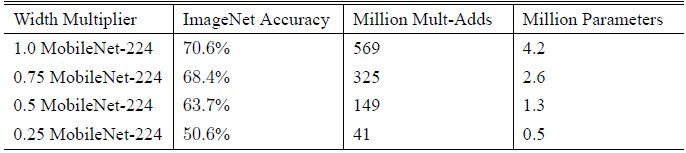
-
$\rho$ 是个 resolution multiplier, 目的是降低 imput image 的尺度以减少计算复杂度(大概$\rho^2$)和参数数量的作用,其取值范围为 $(0,1]$, 其中 $\rho=1$ 代表 baseline MobileNet。Table 3 对比了 resolution multipliers $\rho$ 大小对网络性能的影响:
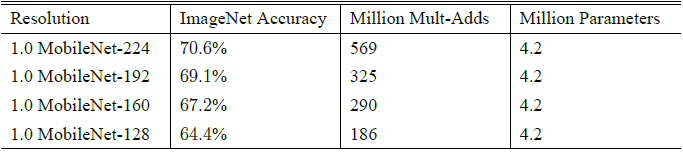
8.2 MobileNet V2
MobileNet V2 则可以理解为 Depthwise Separable Convolution + ResNet。
在最早的 Network in Network 工作中, 1x1 PW 卷积被作为一个降维的操作而引入,后来逐渐发展为 Depthwise Separable Convolution 并被广泛应用,堪称跟 skip-connection 同样具有影响力的网络部件。在 Inception 单元最初提出之时,认为具有较多 channel 的 feature map 是可以压缩的,作者引入 PW 卷积将它们映射到低维(较少 channel 数)空间上并添加多路径处理的范式。之后的 Xception、MobileNet 等工作则将可分离卷积应用到极致:前者指出可分离卷积背后的假设是跨channel相关性和跨spatial相关性的解耦,后者则利用可控的两个超参来获得在效率和精度上取得较好平衡的网络。
8.2.1 Linear Bottlenecks
文中,经过激活层后的张量被称为兴趣流形,具有维HxWxD,其中D即为通常意义的channel数,部分文章也将其称为网络的宽度(width)。
根据之前的研究,兴趣流形可能仅分布在激活空间的一个低维子空间里,利用这一点很容易使用 1x1 PW 卷积将张量降维(即 V1的工作),但由于ReLU的存在,这种降维实际上会损失较多的信息。作者做了一个信息重构的实验,实验结论就是:激活函数在高维空间能够有效的增加非线性,而在低维空间时则会造成较大的信息损失。如下图 Figure 31 所示:当原始输入维度数增加到 15 以后再加 ReLU,基本不会丢失太多的信息;但如果只把原始输入维度增加至 $2\sim 5$ 后再加 ReLU,则会出现较为严重的信息丢失。因此执行降维的卷积层后面不会接类似于 ReLU 这样的非线性激活层。

图31: Examples of ReLU transformations of low-dimensional manifolds embedded in higher-dimensional spaces. In these examples the initial spiral is embedded into an $n$-dimensional space using random matrix $T$ followed by ReLU, and then projected back to the 2D space using $T^{-1}$. In examples above $n = 2, 3$ result in information loss where certain points of the manifold collapse into each other, while for $n = 15$ to $30$ the transformation is highly non-convex.
8.2.2 Depthwise Separable Convolutions
作者通过图 Figure 32 描述了深度可分离卷积的演化史:Figure 32(a) 中普通卷积将 channel 和 spatial 信息同时进行映射,参数量较大;Figure 32(b) 为可分离卷积,解耦了 channel 和 spatial,有一定比例的参数节省;Figure 32(c) 中进行可分离卷积后又添加了 bottleneck,映射到低维空间中;Figure 32(d) 则是从低维空间开始,进行可分离卷积时扩张到较高的维度(前后维度之比被称为expansion factor,扩张系数),之后再通过1x1卷积降到原始维度。
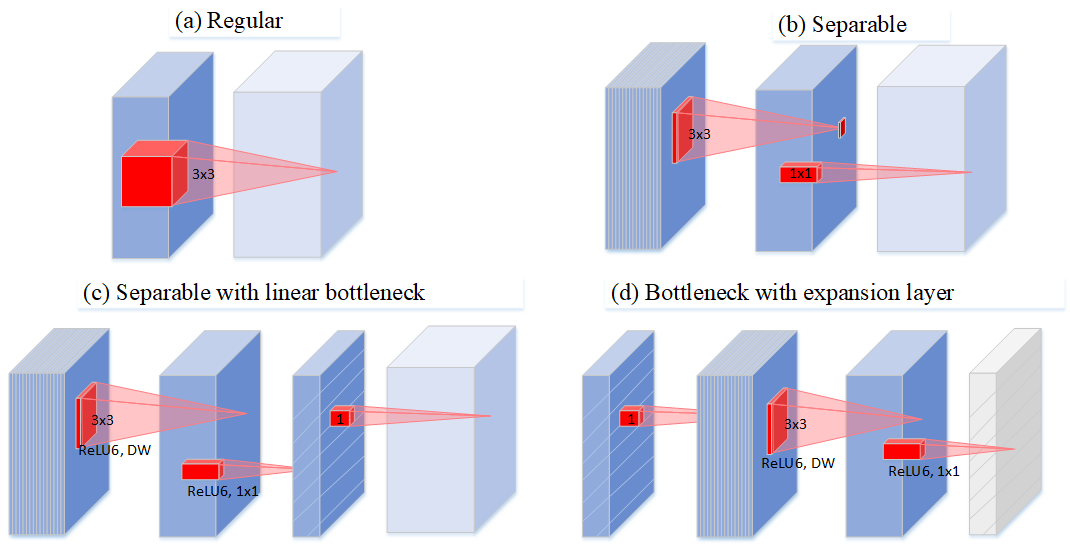
图32: Evolution of separable convolution blocks. The diagonally hatched texture indicates layers that do not contain non-linearities. The last (lightly colored) layer indicates the beginning of the next block. Note: 2d and 2c are equivalent blocks when stacked. Best viewed in color.
继续上面信息损耗的话题,深度可分离卷积大大降低参数量的同时也带来了信息损失的风险。V2 采用了 Figure 22(d) 的类似结构(区别在于最后一层无激活函数),考虑到 DW 卷积的计算特性决定它自己没有改变通道数的能力,因此,给每个 DW 之前都配备了一个 PW,专门用来升维,定义升维系数 $t = 6$,这样不管输入通道数 $C_{in}$ 是多是少,经过第一个 PW 升维之后,DW 都是在相对的更高维 ($t \cdot C_{in}$) 进行工作的。因此可以发现,V2 结构里每个 Bottleneck 的输入通道都很小,并按照 “扩张 - 变换 - 压缩” 的形式搭建模型。
8.2.3 Inverted Residuals
为了提升网络结构的性能,综合上面的两个改进,作者还引入了 {\color{red}ResNet} 结构,构成了作者所说的 Inverted Residual,如 Figure 33(b) 所示。
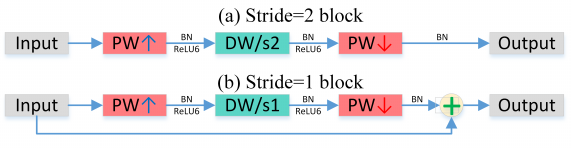
图33: Mobilenet V2.
以前大多数的模型结构加速的工作都停留在压缩网络参数量上。其实这是有误导性的:参数量少不代表计算量小;计算量小不代表理论上速度快(带宽限制)。ResNet 的结构其实对带宽不大友好:旁路的计算量很小,eltwise+ 的特征很大,所以带宽上就比较吃紧。而 Inverted residual 由于 eltwise+ 的特征较小的原因,缓解了这一问题。
8.2.3 Network
整个 V2 的网络结构,如 Table 4 所示:
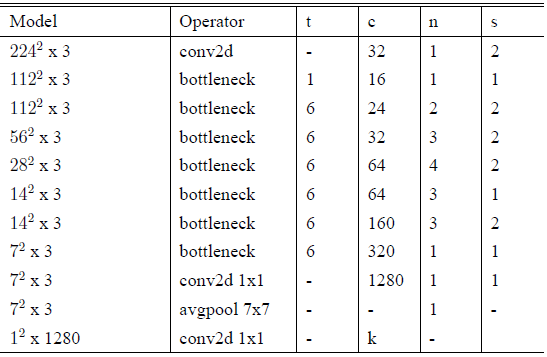
表4: MobileNetV2 : Each line describes a sequence of 1 or more identical (modulo stride) layers, repeated n times. All layers in the same sequence have the same number c of output channels. The first layer of each sequence has a stride s and all others use stride 1. All spatial convolutions use 3x3 kernels. The expansion factor t is always applied to the input size by first PW.
8.3 MobileNet V3
9. ShuffeNet
9.1 ShuffeNet V1
9.1.1 Shuffe units
ShuffleNet V1 可以理解为进一步加强对 Group Conv 和 DW 的使用程度。该论文认为 Xception 里 DW 之后的 PW 计算量太大了,何不也换成 1x1 的 DW 。但是,如果多个 group convolutions 叠加在一起,就会产生一个副作用:某一通道的输出只来自一小部分输入 channels。
Figure 34(a) 为两组叠加卷积层的情况。很明显,某个组的输出只与组内的输入相关。这会阻塞通道组之间的信息流并削弱特征表示。
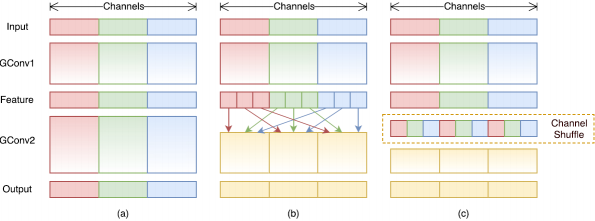
如 Figure 34(b),如果我们让 Group Conv 的输入来自不同的 group(其实 LeNet5 里就是这样的),那么输入和输出通道间信息就可以完全连接起来了。实际操作时有个效率问题,进行每个 group 计算时都要把整个 input feature 加载进来。因此按照图 Figure 34(c),可以事先将输入的 input feature 通过 reshape, transpose and flatten 操作来进行 Channel Shuffle(借鉴了 AlexNet 训练时候的方法),然后计算输出的 feature map 的时候,只要导入需要的输入的 feature map 而不是进行全局索引。
利用 Channel Shuffle 的特性,本文设计了一个 ShuffleNet Unit。基础网络是ResNet-18,如 Figure 36(a),这是一个 residual block,第一个 1x1 的 PW 用来降维,后面的 3x3 是一个 DW,随后跟着一个 1x1 的 PW 升维。我们在设计时,将第一个 1x1 的 PW 替换成 pointwise group conv,随后通过 Channel Shuffle 操作送给 3x3 的 DW,最后一个 pointwise group conv 目的是升维。为了方便,作者没有在第二个 PW layer 后面加上 Channel Shuffle 操作,因为对性能没有提升。其他改动方面,作者没有在 DW 层加上 ReLU。对于 stride=2 的情况下,作者增加了一个 average pooling 和改变了 element wise add 为 concat 操作。

虽然 DW 的理论计算量很低,但在实际低功耗硬件上比较难高效实现。因此作者只在 bottleneck feature maps 上使用。
9.1.2 Network Architecture
如 Table 5,完整网络包含 16 个 ShuffleNer units。分为 3 个 stage(stage2$\sim$stage4),每个 stage 的第一个 block 采用 stride=2 将 feature map 空间尺寸减半。每下一个 stage,通道数加倍。同 ResNet 一样,每个 ShuffleNet unit 里, bottleneck 的通道数是输出通道数的 1/4。在 ShuffleNet units 里,通过 g (group number) 来控制 PW 的 connection sparsity。表中展示了不同的 g 对性能的影响,可以发现 group number 越大,在保持计算量基本不变的前提下允许的通道数越多,网络越“宽”,潜在地有利于网络编码更多的信息,提升模型的性能。实验中还增加了一个网络“宽度”缩放因子 S,来控制各层通道数目,实现网络自定义。将 Table 5 中的网络定义为 "ShuffleNet 1x”, "ShuffleNet Sx” 意味着将 "ShuffleNet 1x" 的通道数降低为 S 倍。
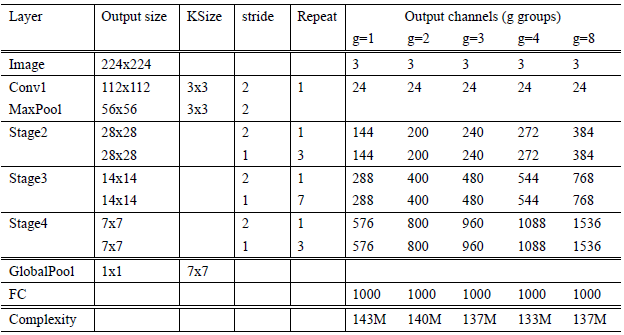
表5: ShuffleNet architecture. The complexity is evaluated with FLOPs, i.e. the number of floating-point multiplication-adds. Note that for Stage 2, we do not apply group convolution on the first pointwise layer because the number of input channels is relatively small.
9.2 ShuffeNet V2
10. EfficientNet
11. MixConv
12. Related link
坑太多,有时间再来填







