二分查找算法【配合经典力扣题目讲解】（C++实现）_c++二分算法

1 二分查找的基本原理

二分查找的使用情况：对于已经有序的数据来说，二分查找可以极大的提高查找效率，我们知道查找的本质就是排除，为什么二分查找可以右极高的查找效率呢？本质就是一次查找就可以排除一半无效的数据，这就是它高效的原因之一；
从时间复杂度度的角度来说：二分查找的查找效率达到 O（log n）,这比遍历一遍数据的查找方式的时间复杂度O(n)好很多;特别是体现在数据量极大的情况下；

---

二分查找的原理也就是：要查找某一个数x，前提查找的数据是有序的，那么就可以找到该有序数据的中间位置middle，用x和middle比较，如果x比middle大，那么说明，x在middle的右边，那么就排除middle左边的所有数据（包括middle本身）；如果x比middle小，那么说明，x在middle的左边，那么就可以排除middle右边的所有数据（包括middle本身）；如果x == middle等于那么就说明找到了x；

---

2 二分查找算法的两种写法

大家对二分擦或者算法总有一种一看就会一写就废的感觉；
主要是对查找的边界控制得不够清晰；
对于边界的控制有左闭右闭的写法，也有左闭右开的写法；
两种写法都是有些微的差别，但是原理是一样的；

---

2.1 左闭右闭的二分查找写法

void binary_search(vector<int> nums,int x)
{
// 定义左闭右闭的区间里，[left, right]
	int left = 0;
    int right = nums.size() - 1; 
    // 当left==right，区间[left, right]依然有效，所以用 <=
     while (left <= right) {
     	int middle = left + ((right - left) >>1);
            if (nums[middle] > x) {
            // x 在左区间，所以[left, middle - 1]
                right = middle - 1; 
            } else if (nums[middle] < target) {
            // target 在右区间，所以[middle + 1, right]
                left = middle + 1; 
            } else { // nums[middle] == target
                 // 数组中找到目标值
            }
        }
        //退出循环表示：left>right此时
        // 未找到目标值
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

---

我们重点关注循环的边界条件：while(left<=right),为什么要用<=，而不用<，其实就是因为我们用的是左闭右闭区间的写法，此时让left==right 时候，还在区间范围内，所以要继续查找;

---

2.2 左闭右开的区间的写法

void binary_search(vector<int> nums,int x)
{
// 定义左闭右闭的区间里，[left, right)
	int left = 0;
    int right = nums.size(); //注意这里的right是比数组最后一个值的下标还多1的下标
    // 当left==right，区间[left, right）无效，所以用 <
     while (left < right) {
     	int middle = left + ((right - left) >>1);
            if (nums[middle] > x) {
            // x 在左区间，所以[left, middle)
            //注意这里和闭区间的写法不一样
                right = middle; 
            } else if (nums[middle] < target) {
            // target 在右区间，所以[middle + 1, right)
                left = middle + 1; 
            } else { // nums[middle] == target
                 // 数组中找到目标值
            }
        }
        //退出循环表示：left>right此时
        // 未找到目标值
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

而我们的左闭右开区间的写法：相比于左闭右闭区间的写法，在while的判断条件有所不同，还有当 x < 中间值时候，right = middle，而不是right = middle-1;因为开区间，说明middle本身就不是在数据方位内的值了，所以不用-1；

---

3 四道经典力扣的二分算法的题目

3.1 有效的完全平方数

---

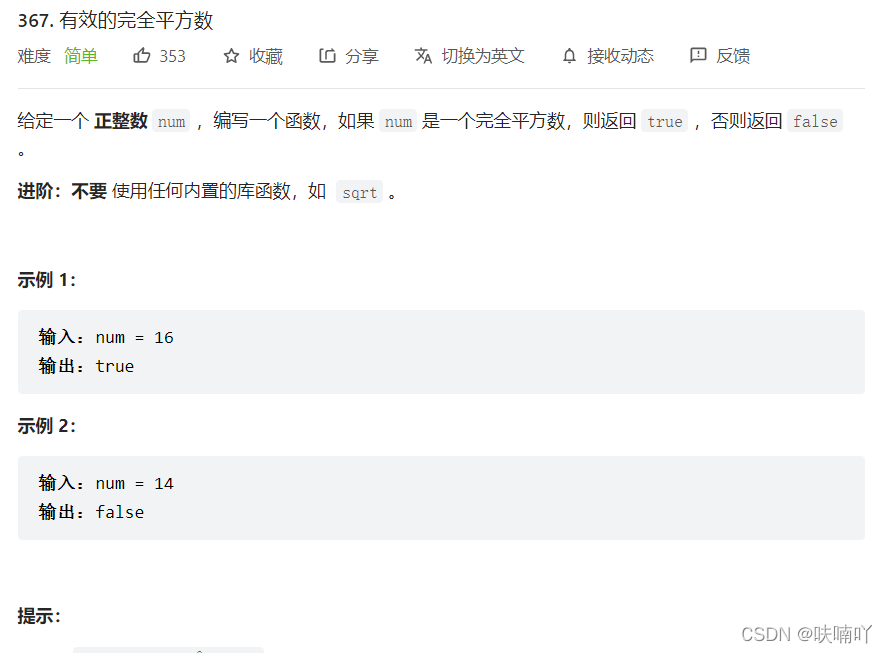
思路：只要我们在[1,num]的范围内，试数，找到一个数x ,只要满足x*x = num，那么就可以了；
此时，由于【1，num】的数都是升序，即有序，我们可以使用二分查找算法，这样查找效率更高；

---

代码：

class Solution {
public:
//只要在[1,num]的区间不断试数就可以
    bool isPerfectSquare(int num) {
        int left = 1;
        int right  =num;

        while(left <=right)
        {
            long long middle = left +((right - left)>>1);

            long long val = middle*middle;
            if(val == num)
                return true;
            else if(val < num)
                left = middle+1;
            else
                right = middle -1;
            
        }
        return false;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

---

3.2 x 的平方根

---

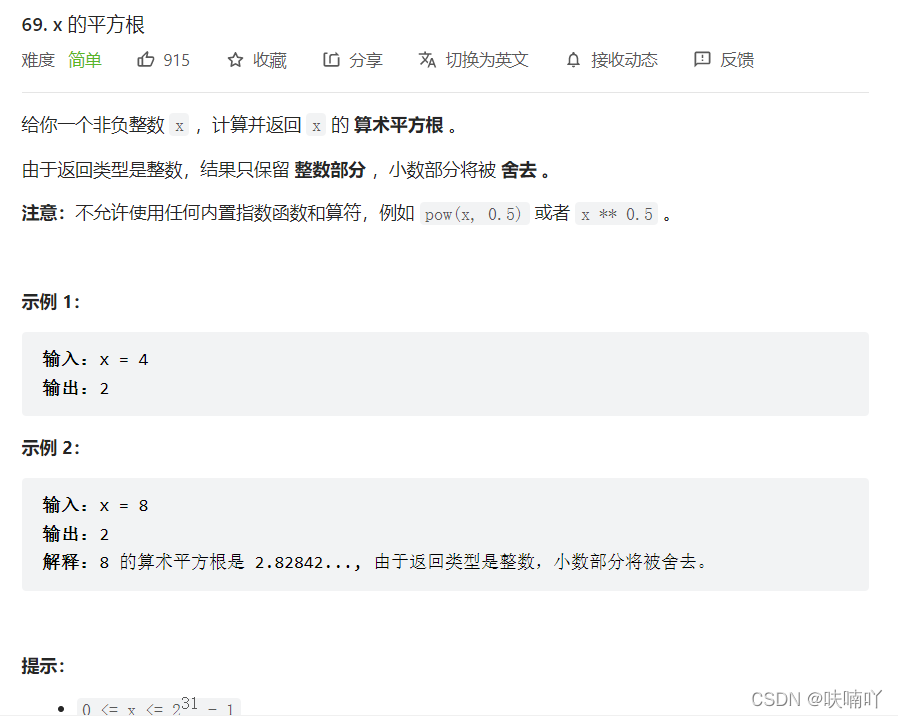
思路：
依旧是，在[0,x]中找到一个数，k,只要满足kk <= x，
那么就可以说明当kk = x，k就是x的算术平方根；
当k*k<x，那么说明k可能是x的算术平方根（题目的要求小数点的数会被舍掉，所以说，k * k< x是有可能成为x的算术平方根的值）；
当k > x那么直接pass掉；
由于这个又是在[0,x]升序查找，所以说：我们还是用二分查找算法解决；

---

代码

class Solution {
public:
    int mySqrt(int x) {

        //在[0,x]中不断试数，算出结果
        //找到一个数k,满足k*k <= x即可
        int left = 0;
        int right = x; 
        int ret = -1; //保存结果的值
        while(left <=right)
        {
            int middle = left + ((right-left)>>1);
            if((long long)middle*middle<=x)
            {
                ret = middle;//由于<的情况也有可能找到ret，所以就保存该middle值
                left = middle+1;
            }
            else
            {
                right = middle -1;
            }
         }
         return ret;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

---

3.3 搜索插入位置

---

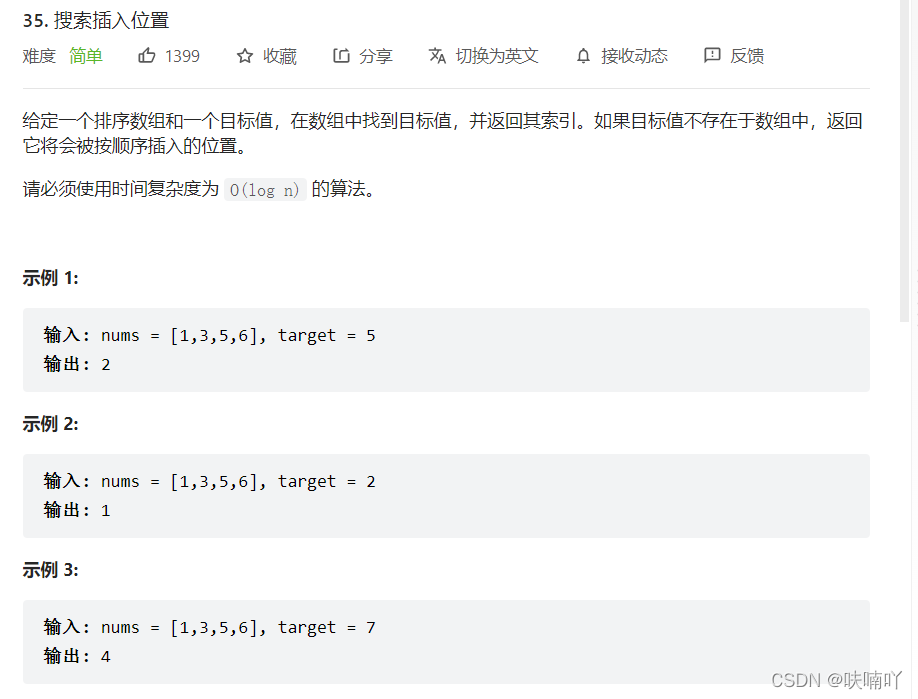
有序的数据，毫无疑问，直接二分算法：

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
		//注意我这里是左闭右开的区间
        int left = 0;
        int right = nums.size();

        while(left < right)
        {
            int middle = left +((right - left)>>1);

            if(target<nums[middle])
            {
                right = middle;
            }
            else if ( target > nums[middle])
            {
                left = middle +1;
            }
            else
            {
                return middle;
            }
        }
        //1.头插，比[1,2,3],插入0，
        //2.尾插，比如[1,2,3]插入4，
        //3.插中间，比如[1,2,4]插入3
        return right;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

---

3.4 在排序数组中查找元素的第一个和最后一个位置

---

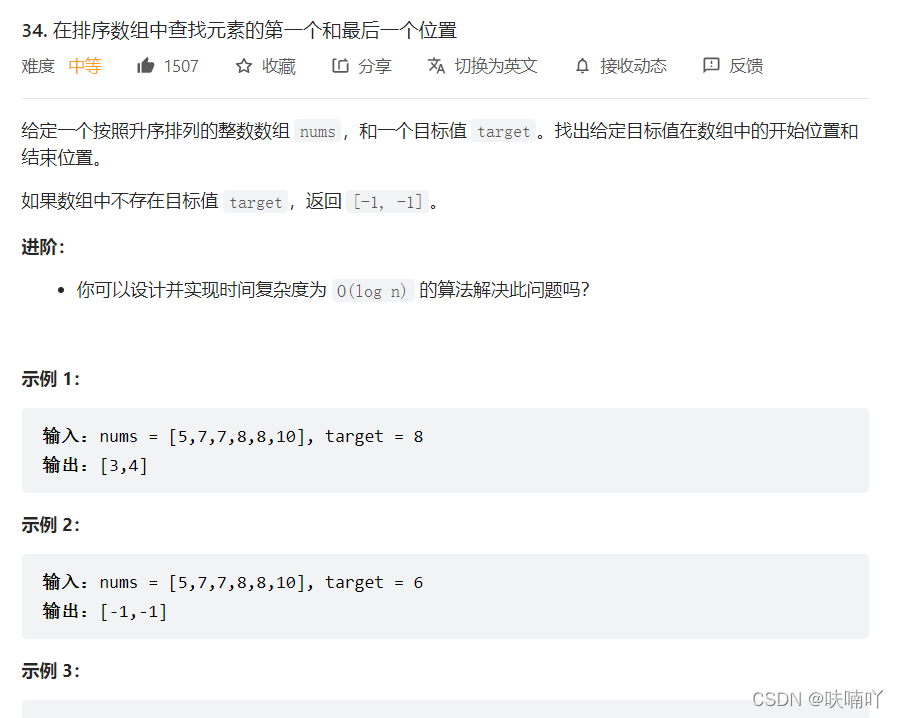
二分算法不多说：
主要是我们要如何找到第一个数位置，和最后一个数位置：
首先我们得清楚，当我们找第一个数位置时候，需要把一种情况：即二分查找时候，target == nums[middle]时候得条件，也需要让 right = middle -1;的操作，这样才可以把最后一个数的位置给避开；
反之亦然，也就是说，擦或者最后一个数时候，也是这样操作；

---

代码：

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        //先找到第一个值的最左下标
        int left = LeftIndex(nums,target);
          //在找最后一个值的最右下标
        int right = RightIndex(nums,target);
        if(right < left )
            return vector<int>{-1,-1};
        //right >=left,
        //大于情况就是正常的有多个相同的目标值，
        //等于的情况就是数组只有一个数
        return vector<int>{left,right};


    }
    int LeftIndex (vector<int>&nums ,int target)
    {
        int left = 0;
        int right = nums.size() - 1;

        while(left <= right)
        {
            int middle = left + ((right - left) >> 1);

            if(target <= nums[middle])
                right = middle - 1;
            else
                left = middle + 1;
        }
        //退出循环后，下标区间为【right,left】,而left就是要找的值
        //或者退出循环后，left不是要找的值如【1，7，8，9，10】找 8，
        // 退出循环后下标位置在left = 2;  right = 1
        return left;
    }
    int RightIndex (vector<int>&nums,int target)
    {
          int left = 0;
        int right = nums.size() - 1;
         while(left <= right)
        {
            int middle = left +( (right - left) >> 1);

            if(target >=nums[middle]) //大于等于的条件就继续移动左下标，直到退出循环
                left = middle + 1;
            else
                right = middle - 1;
        }
        //退出循环后，下标区间为【right,left】,而right就是要找的值
        return right;
    }
};

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53

---