LoRA, 替代 fine-tune 的轻量级低秩分解_lora矩阵分解

一. 整体介绍

LoRA, Low-Rank Adaptation of Large Language Models, 大语言模型的低秩适配器.
这里的秩就是通用的 最大线性无关组个数 这样的定义.
适用场景: 用 Lora 来替代大模型的常规 fine-tune.
优点:

1. 冻结原模型, 只需更新很少的参数, 减轻计算与存储的压力.
2. 插拔式的工作方式, 可以共用基座, 部署时一个进程内可灵活地完成多任务预测.
3. 评测结果好, 比 adapter, prefix-tuning, and fine-tuning 等其他下游任务的学习方式指标更好.

二. 方法思想

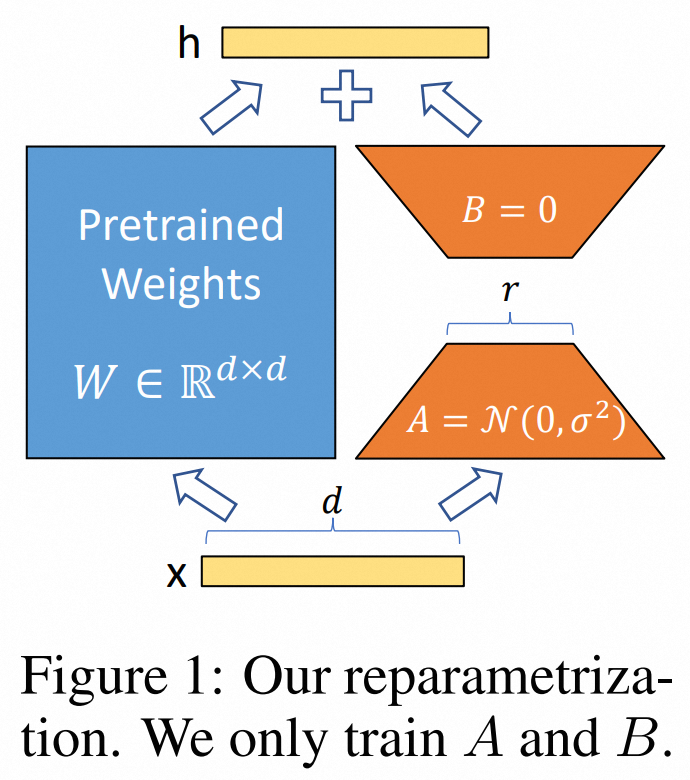
对于一个预训练的权重矩阵 $W_0\in {\mathbb{R}}^{d\times k}$, 将它的更新限制为低秩分解的形式,
$$W^{(新)}=W_0+\Delta W=W_0+BA\text{\hspace{1em}(1)}$$
$whereB\in {\mathbb{R}}^{d\times r},A\in {\mathbb{R}}^{r\times k},r<<min(d,k)$,
这样该模块的输出就是
$$h=W_{0}x+\Delta Wx=W_{0}x+BAx\text{\hspace{1em}(2)}$$

tips: 矩阵乘法满足结合律, 即 (AB)C=A(BC) .

三. 源码解读

首先定义了 LoRALayer 类, 只是维护了几个self.xx字段:

• r, rank 参数
• lora_alpha,
• lora_dropout,
• merge_weights, 是否直接将原 W0 变为 W(新), 这样没有任何额外计算代价.

然后以最常用的 Linear 讨论.

1. init() 中构造 lora_A lora_B 两个矩阵并注册为网络参数.
2. forward() 中按照 上文式(2) 作实现, 但存在 $BAx$ 与 $xAB$ 的写法差异.

class LoRALayer():
    def __init__(
        self, 
        r: int, 
        lora_alpha: int, 
        lora_dropout: float,
        merge_weights: bool,
    ):
    self.xx=xx
    pass

class Linear(nn.Linear, LoRALayer):
  def __init__(self, in_features: int, out_features: int, r:int=0):
        nn.Linear.__init__(self, in_features, out_features, **kwargs)
        LoRALayer.__init__(self, r=r, lora_alpha=lora_alpha, lora_dropout=lora_dropout, merge_weights=merge_weights)
        if r > 0:
            self.lora_A = nn.Parameter(self.weight.new_zeros((r, in_features)))
            self.lora_B = nn.Parameter(self.weight.new_zeros((out_features, r)))
            self.scaling = self.lora_alpha / self.r

    def forward(self, x: torch.Tensor):
        result = F.linear(x, T(self.weight), bias=self.bias)
        if self.r > 0:
            # @ 运算符对应的是 __matmul__(self, x) 实现.
            result += (self.lora_dropout(x) @ self.lora_A.transpose(0, 1) @ self.lora_B.transpose(0, 1)) * self.scaling
        return result
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

3.1 如何使用

把原模型中使用到 nn.Linear 的语句, 直接替换为 lora.Linear, 就是这么简洁!
因为 lora.Linear 使用了多继承, 把原 linear 的 weight 也包含进去了, 名字也没改, 所以 无脑restore 也不会有不一致问题.

同时, 插件名字含有 ‘lora_A, lora_B’, 所以无论保存还是计算梯度时, 都可以靠字符串规律简单的单拎出来.

四. 使用例子

有两个例子, 都是用在了 transformer block 内 multi_head_attention 中的 qkv parameter 中.

4.1 gpt-2

以官方的 GPT2Model 改造为例.

class Attention(nn.Module):
    def __init__(self, nx, n_ctx, config, scale=False):
        super(Attention, self).__init__()
        n_state = nx  # in Attention: n_state=768 (nx=n_embd)
        # [switch nx => n_state from Block to Attention to keep identical to TF implem]
        
        assert n_state % config.n_head == 0
        self.register_buffer("bias", torch.tril(torch.ones(n_ctx, n_ctx)).view(1, 1, n_ctx, n_ctx))
        self.n_head = config.n_head
        self.split_size = n_state
        self.scale = scale
        self.c_attn = lora.MergedLinear(
            nx, n_state * 3, 
            r=config.lora_attn_dim, 
            lora_alpha=config.lora_attn_alpha, 
            lora_dropout=config.lora_dropout, 
            enable_lora=[True, False, True], 
            fan_in_fan_out=True,
            merge_weights=False
        )
        self.c_proj = Conv1D(n_state, nx)
        self.config = config
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

4.2 RoBertA

这个更直观一点.

class RobertaSelfAttention(nn.Module):
    def __init__(self, config):
        if config.apply_lora:
            self.query = lora.Linear(config.hidden_size, self.all_head_size, config.lora_r, lora_alpha=config.lora_alpha)
        else:
            self.query = nn.Linear(config.hidden_size, self.all_head_size)
1
2
3
4
5
6

4.3 与 layer_norm, bias, activation 的耦合关系?

通过例子看到, lora 只介入 linear 层的 $X{W}^T$ 计算, 之后再原样加回 bias.
再之后是 soft_max 对权重归一化, 然后与 value 向量相乘. 然后是 layer_norm.

五. 自己的 tf 1.12 实现

# coding: utf-8

import tensorflow as tf
from tensorflow.contrib import keras
from tensorflow.python.framework import tensor_shape


class Dense(keras.layers.Dense):
    """
    这里也取名 Dense, 与 keras.layers.Dense 同名, 如此 weight 的变量名也不会受到影响.
    """

    def __init__(self,
                 r=32,
                 lora_alpha=1,
                 **kwargs):
                 
        if 'input_dim' in kwargs:
            self.in_features = kwargs['input_dim']
        if 'units' in kwargs:
            self.out_features = kwargs['units']
        self.r = r
        self.lora_alpha = lora_alpha
        # 兼容 py2, 避免值为 0
        self.scaling = lora_alpha * 1.0 / r
        self.lora_A = None
        self.lora_B = None
        keras.layers.Dense.__init__(self,
                                    **kwargs)

    def build(self, input_shape):
        keras.layers.Dense.build(self, input_shape)
        input_shape = tensor_shape.TensorShape(input_shape)
        if not hasattr(self, 'in_features'):
            self.in_features = input_shape[-1].value
        self.lora_A = self.add_weight(name='lora_A', shape=[self.r, self.in_features],
                                      initializer=keras.initializers.he_uniform())
        self.lora_B = self.add_weight(name='lora_B', shape=[self.out_features, self.r],
                                      initializer=keras.initializers.Zeros)

    def call(self, inputs):
        result = keras.layers.Dense.call(self, inputs)
        tmp = tf.matmul(inputs, tf.transpose(self.lora_A, perm=[1, 0]))
        tmp = tf.matmul(tmp, tf.transpose(self.lora_B, perm=[1, 0]))
        result += tmp * self.scaling
        return result

    def __repr__(self):
        return "(group_tag={}, A={} ,B={})".format(self.group_tag, self.A, self.B)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

六. 梯度注意事项

1. scaling = lora_alpha / r 是个小于1的正数, 一定避免0值, 否则梯度永远是 0 !
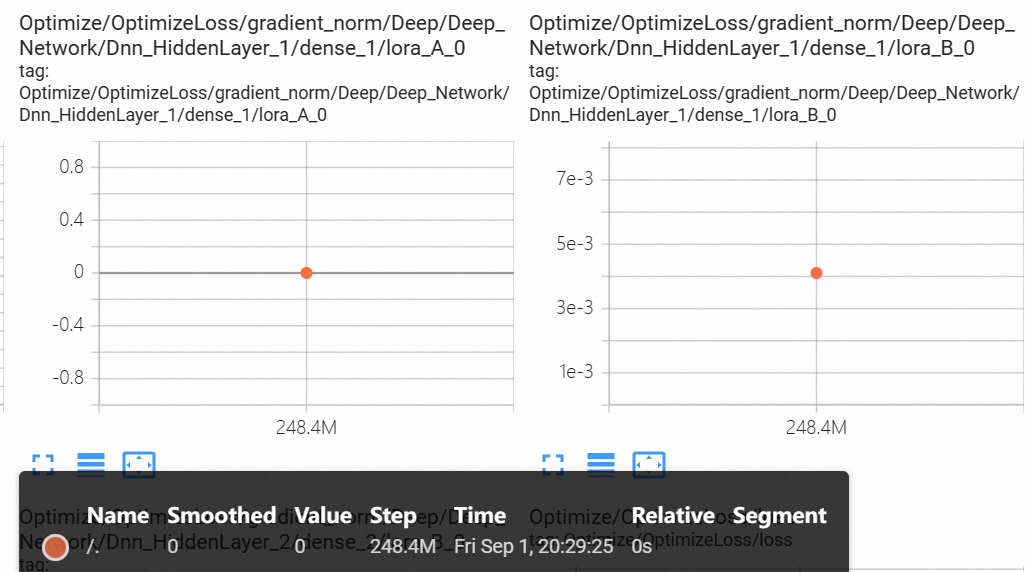
2. lora_A 在 step=1 时的梯度为0, 因为 lora_B 初始化为全 0. 给个实操的例子做验证:

参考

1. paper, LoRA: Low-Rank Adaptation of Large Language Models
   
2. github repo, LoRA