八大排序算法（java实现） 冒泡排序 快速排序 堆排序 归并排序 等_程序就排序冒泡背包分治

• 八大排序算法
  • 一、直接插入
    - 1.基本思路
    - 2.代码实现
    - 3.时间复杂度和空间复杂度
  • 二、希尔排序
    - 1.基本思路
    - 2.代码实现
    - 3.时间复杂度和空间复杂度
  • 三、简单选择
    - 1.基本思路
    - 2.代码实现
    - 3.时间复杂度和空间复杂度
  • 四、堆排序
    - 1.基本思路
    - 2.代码实现
    - 3.时间复杂度和空间复杂度
  • 五、冒泡排序
    - 1.基本思路
    - 2.代码实现
    - 3.时间复杂度和空间复杂度
  • 六、快速排序
    - 1.基本思路
    - 2.代码实现
    - 3.时间复杂度和空间复杂度
  • 七、归并排序
    - 1.基本思路
    - 2.代码实现
    - 3.时间复杂度和空间复杂度
  • 八、基数排序
    - 1.基本思路
    - 2.代码实现
    - 3.时间复杂度和空间复杂度
  • 总结

八大排序算法

一、直接插入

1.基本思路

在要排序的一组数中，假设前面(n-1) [n>=2] 个数已经是排好顺序的，现在要把第n个数插到前面的有序数中，使得这n个数也是排好顺序的。如此反复循环，直到全部排好顺序。

2.代码实现

• 1.遍历数组，每次循环从第二个数字往前插入
• 2.设定插入数和得到已经排好序列的最后一个数的位数。temp和j=i-1。
• 3.从最后一个数开始向前循环，如果插入数小于当前数，就将当前数向后移动一位。

public static void insertSort(int[] data) {
    int temp;
    for(int i = 1;i < data.length; i++){// 取第i个数,插入前边的有序的序列
        temp = data[i];
        int j;
        for(j = i - 1; j>=0; j--) {// 从第i-1的位置上开始比较
            if(data[j] > temp) {// 若前面的数大，则往后挪一位
                data[j+1] = data[j];
            } else {
                break;// 否则，说明要插入的数比较大
            }
        }
        data[j+1] = temp;// 找到这个位置，插入数据
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

3.时间复杂度和空间复杂度

直接插入排序的平均复杂度为O(n²)，最坏时间复杂度：O(n²)，空间复杂度：O(1)，没有分配内存。

二、希尔排序

针对直接插入排序下的效率问题，有人对此进行了改进与升级，这就是现在的希尔排序。希尔排序，也称递减增量排序算法，是插入排序的一种更高效的改进版本。希尔排序是非稳定排序算法。

1.基本思路

• 1.数的个数为length，i=length/2，将下标差值为i的数分为一组，构成有序序列。

• 2.再取i=i/2 ，将下标差值为i的数分为一组，构成有序序列。

• 3.重复第二步，直到k=1执行简单插入排序。

思路：

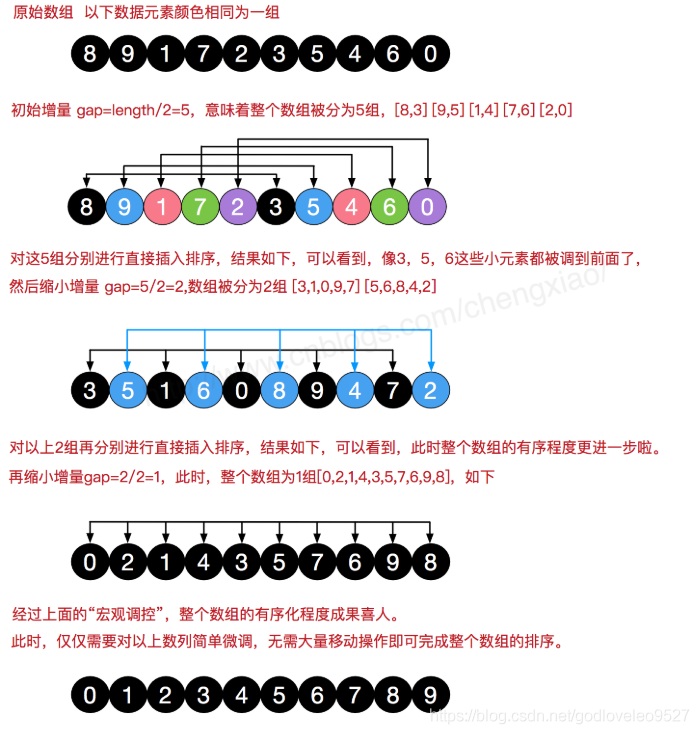
• 1.希尔排序（shell sort）这个排序方法又称为缩小增量排序，是1959年D·L·Shell提出来的。该方法的基本思想是：设待排序元素序列有n个元素，首先取一个整数increment（小于n）作为间隔将全部元素分为increment个子序列，所有距离为increment的元素放在同一个子序列中，在每一个子序列中分别实行直接插入排序。然后缩小间隔increment，重复上述子序列划分和排序工作。直到最后取increment=1，将所有元素放在同一个子序列中排序为止。
• 2.由于开始时，increment的取值较大，每个子序列中的元素较少，排序速度较快，到排序后期increment取值逐渐变小，子序列中元素个数逐渐增多，但由于前面工作的基础，大多数元素已经基本有序，所以排序速度仍然很快。

希尔排序举例：

2.代码实现

• 1.遍历数组，每次循环从第二个数字往前插入
• 2.设定插入数和得到已经排好序列的最后一个数的位数。temp和j=i-1。
• 3.从最后一个数开始向前循环，如果插入数小于当前数，就将当前数向后移动一位。

（1）首先确定每一组序列的下标的间隔，循环每次需要的间隔：int i = length/2; i >0 ; i /= 2

（2）然后将每一组序列中元素进行插入排序，第二组第一个插入的数字是第一组第一个插入数字之后的那个数组，从i之后每个数字都要进行插入排序，就是插入的序列是各自不同的序列，不是一个一个子序列循环，而是在一个循环中for (int j=i;j<length;j++)完成所有子序列的插入排序。

（3）直到i=0为止。

public static void shellSort(int[] array) {
    int length = array.length;
    for (int i = length / 2; i > 0; i /= 2) {//序列的间隔，一直到间隔为一，这时候就只有一个子序列
        for (int j = i; j < length; j++) {//从i之后每个数字都要进行插入排序，就是插入的序列是各自不同的序列
            int temp = array[j];//里面就是直接插入算法
            int k;
            for (k = j - i; k >= 0; k -= i) {//实现各个数字插入排序到不同的序列中，直到间隔为1的时候，只有一个序列，就是完全的一个直接插入排序
                if (temp < array[k]) {
                    array[k + i] = array[k];
                } else {
                    break;
                }
            }
            array[k + i] = temp;//把数字插入到位置上
        }
    }
    System.out.println(Arrays.toString(array));
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

3.时间复杂度和空间复杂度

希尔排序的平均时间复杂度为O(n²)，空间复杂度O(1) 。

三、简单选择

1.基本思路

基本原理如下：对于给定的一组记录，经过第一轮比较后得到最小的记录，然后将该记录的位置与第一个记录的位置交换；接着对不包括第一个记录以外的其他记录进行第二次比较，得到最小记录并与第二个位置记录交换；重复该过程，直到进行比较的记录只剩下一个为止。

2.代码实现

• 1.确定要插入最小值的位置，从0开始到最后int i = 0; i <len ; i++
• 2.将每次开始位置上的数字暂定为最小值min,从开始数字之后一个个和min比较，再把最小值存放到min
• 3.将最小值所在位置上的数字和开始位置上的数字交换

public static void selectSort(int[] array) {
    int len = array.length;
    for (int i = 0; i < len; i++) {//确定每次开始的位置
        int min = array[i];//设定开始数字为最小的值最小值
        int flag = i;
        for (int j = i + 1; j < len; j++) {//把最小值存放到min,从开始数字向后一个个和min比较，再把最小值存放到min
            if (min > array[j]) {
                min = array[j];
                flag = j;
            }
        }
        if (flag != i) {
            array[flag] = array[i];
            array[i] = min;
        }
    }
    System.out.println(Arrays.toString(array));
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

3.时间复杂度和空间复杂度

简单选择排序的时间复杂度为O(n²)

四、堆排序

1.基本思路

• 1.若array[0，…，n-1]表示一颗完全二叉树的顺序存储模式，则双亲节点指针和孩子结点指针之间的内在关系如下：

任意一节点指针 i：
父节点：i==0 ? null : (i-1)/2
左孩子：2*i + 1
右孩子：2*i + 2
1
2
3
4

• 2.堆得定义

n个关键字序列array[0，...，n-1]，当且仅当满足下列要求：(0 <= i <= (n-1)/2)
① array[i] <= array[2*i + 1] 且 array[i] <= array[2*i + 2]； 称为小根堆；
② array[i] >= array[2*i + 1] 且 array[i] >= array[2*i + 2]； 称为大根堆；
1
2
3

• 3.建立大顶堆

n个节点的完全二叉树array[0，…，n-1]，最后一个节点n-1是第(n-1-1)/2个节点的孩子。对第(n-1-1)/2个节点为根的子树调整，使该子树称为堆。

对于大根堆，调整方法为：若【根节点的关键字】小于【左右子女中关键字较大者】，则交换。

之后向前依次对各节点（(n-2)/2 - 1）~ 0为根的子树进行调整，看该节点值是否大于其左右子节点的值，若不是，将左右子节点中较大值与之交换，交换后可能会破坏下一级堆，于是继续采用上述方法构建下一级的堆，直到以该节点为根的子树构成堆为止。

反复利用上述调整堆的方法建堆，直到根节点。

• 4.堆排序（大顶堆）

①将存放在array[0，...，n-1]中的n个元素建成初始堆；
②将堆顶元素与堆底元素进行交换，则序列的最大值即已放到正确的位置；
③将数组中array[0，...，n-1]前n-1个元素再次形成大根堆，再重复第②③步，直到堆中仅剩下一个元素为止。
1
2
3

2.代码实现

/**
    *  大顶堆排序
    * @param array
    */
public static void maxHeapSort(int[] array) {
    int i;
    int len = array.length;
    // 构建大顶堆
    for (i = len / 2 - 1; i >= 0; i--) {
        adjustMaxHeap(array, i, len);
    }
    // 堆顶是最大值，交换堆顶和最后一个数，再重新调整最大堆，下一次循环   i--
    for (i = len - 1; i >= 0; i--) {
        int temp = array[0];
        array[0] = array[i];
        array[i] = temp;
        adjustMaxHeap(array, 0, i);
    }
    System.out.println(Arrays.toString(array));
}

private static void adjustMaxHeap(int[] a, int pos, int len) {
    int temp;
    int child;
    for (temp = a[pos]; 2 * pos + 1 < len; pos = child) {
        // 数组从0开始，r(i)>=r(2i) r(i)>=r(2i+1)  对应 pos => 2 * pos + 1 和 2 * pos +2
        child = 2 * pos + 1;
        // 有右孩子，且右孩子数值更大
        if (child + 1 < len && a[child] < a[child + 1]) {
            child++;
        }
        // 最大的孩子大于根节点
        if (a[child] > temp) {
            a[pos] = a[child];
        } else {
            break;
        }
    }
    a[pos] = temp;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

3.时间复杂度和空间复杂度

时间复杂度:建堆：o(n)，每次调整o(log n)，故最好、最坏、平均情况下：o(n*logn);

五、冒泡排序

1.基本思路

一次冒泡将序列中从头到尾所有元素两两比较，将最大的放在最后面。

将剩余序列中所有元素再次两两比较，将最大的放在最后面。

重复第二步，直到只剩下一个数。

2.代码实现

/**
 * @author fupeng
 * 冒泡排序优化第二版
 * 第一版优化增加flag标记，没有数字交换直接return，最优时间复杂度O(n)
 * 第二版优化，增加tempPosition记录内循环最后一次交换的位置，来缩减内循环的次数
 */
public static void bubbleSort(int[] array) {
    int len = array.length - 1;
    // 开辟一个临时空间, 存放交换的中间值
    int temp;
    // 记录最后一次交换的位置
    int tempPosition = 0;
    // 要遍历的次数
    for (int i = 0; i < array.length - 1; i++) {
        int flag = 1; // 设置一个标志位
        // 依次比较相邻两个数的大小，遍历一次后，会将前面没有排好序的最大值放到后面位置
        for (int j = 0; j < len; j++) {
            // 比较相邻的元素，如果前面的数大于后面的数，交换
            if (array[j] > array[j + 1]) {
                temp = array[j + 1];
                array[j + 1] = array[j];
                array[j] = temp;
                // 发生交换，标志位置0
                flag = 0;
                // 记录交换的位置
                tempPosition = j;
            }
        }
        // 把最后一次交换的位置给len，来缩减内循环的次数
        len = tempPosition;
        // 如果没有交换过元素，则已经有序
        if (flag == 1) {
            System.out.println(Arrays.toString(array));
            return;
        }
    }
    System.out.println(Arrays.toString(array));
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

3.时间复杂度和空间复杂度

冒泡排序的最好时间复杂度为O(n),最坏时间复杂度为O(n²),平均时间复杂度为O(n²),空间复杂度为O(1),它是一种稳定的排序算法。

六、快速排序

1.基本思路

快速排序使用分治策略来把一个序列（list）分为两个子序列（sub-lists）。步骤为：

• 1.从数列中挑出一个元素，称为"基准"（pivot）。
• 2.重新排序数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准后面（相同的数可以到任一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
• 3.递归地（recursively）把小于基准值元素的子数列和大于基准值元素的子数列排序。

递归到最底部时，数列的大小是零或一，也就是已经排序好了。这个算法一定会结束，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

2.代码实现

public static void quickSort(int[] array) {
    sort(array, 0, array.length - 1);
    System.out.println(Arrays.toString(array));
}

private static void sort(int[] a, int low, int high) {
    int i = low;
    int j = high;
    if (a.length <= 1) {
        return;
    }
    if (i >= j) {
        return;
    }
    int index = a[i];
    while (i < j) {
        while (i < j && a[j] >= index)
            j--;
        if (a[j] < index)
            a[i++] = a[j];
        while (i < j && a[i] <= index)
            i++;
        if (a[i] > index)
            a[j--] = a[i];
    }
    a[i] = index;
    sort(a, low, i - 1);
    sort(a, i + 1, high);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

3.时间复杂度和空间复杂度

虽然 快排的时间复杂度达到了 O(n²)，但是在大多数情况下都比平均时间复杂度为 O(n logn) 的排序算法表现要更好。

七、归并排序

1.基本思路

归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

• 1.分而治之
  

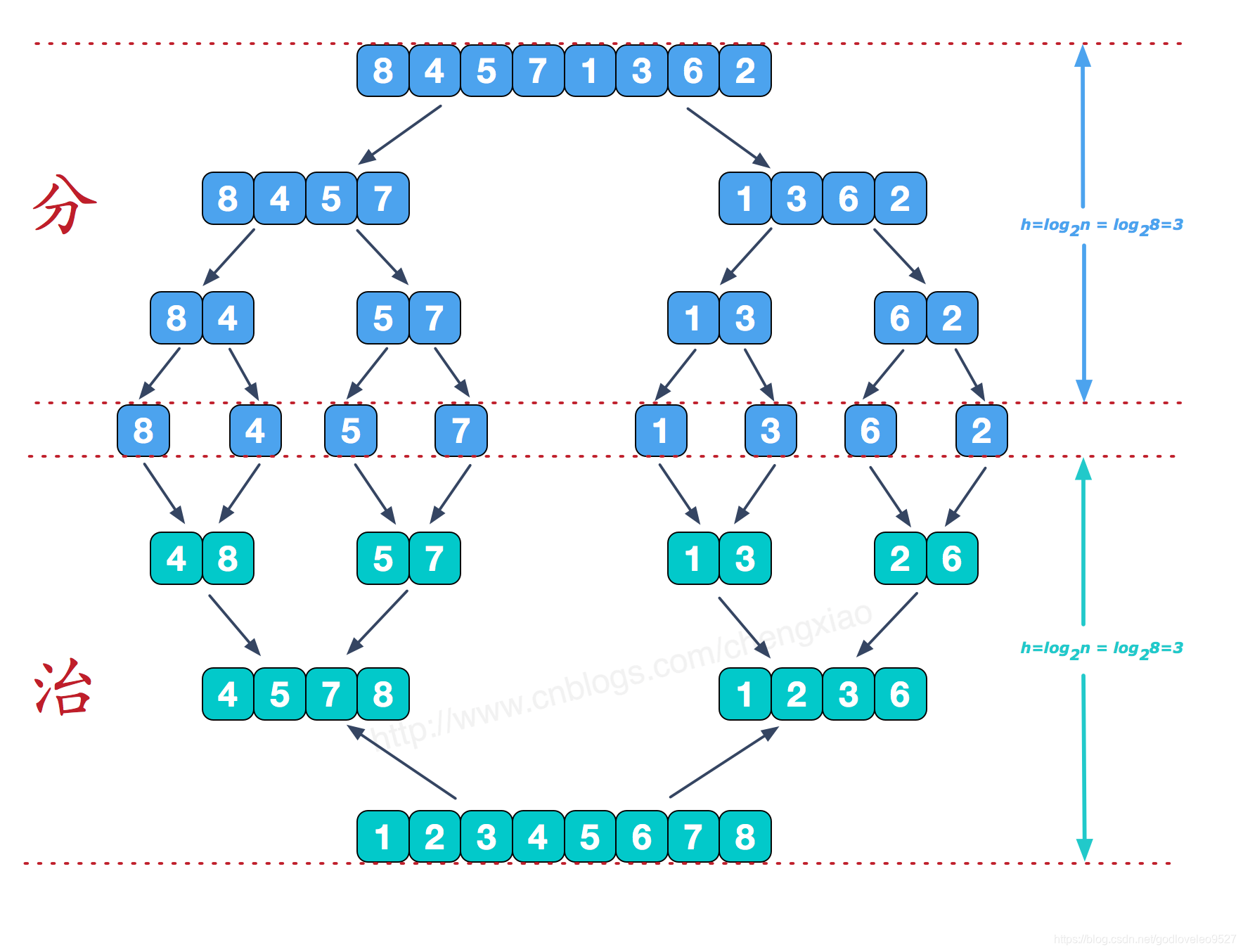
可以看到这种结构很像一棵完全二叉树，本文的归并排序我们采用递归去实现（也可采用迭代的方式去实现）。分阶段可以理解为就是递归拆分子序列的过程，递归深度为log2n。

• 2.合并相邻有序子序列
  再来看看治阶段，我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现步骤。

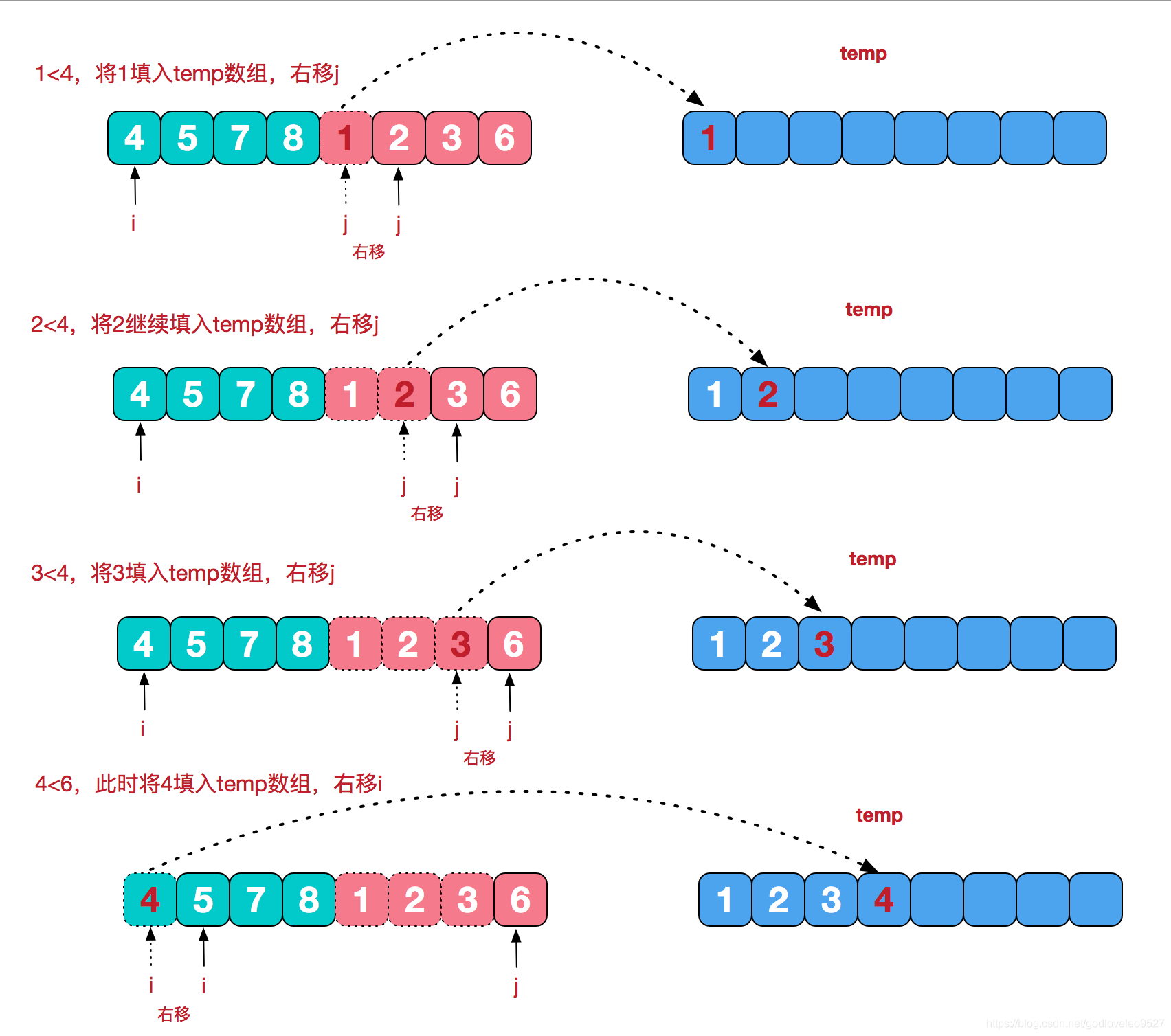
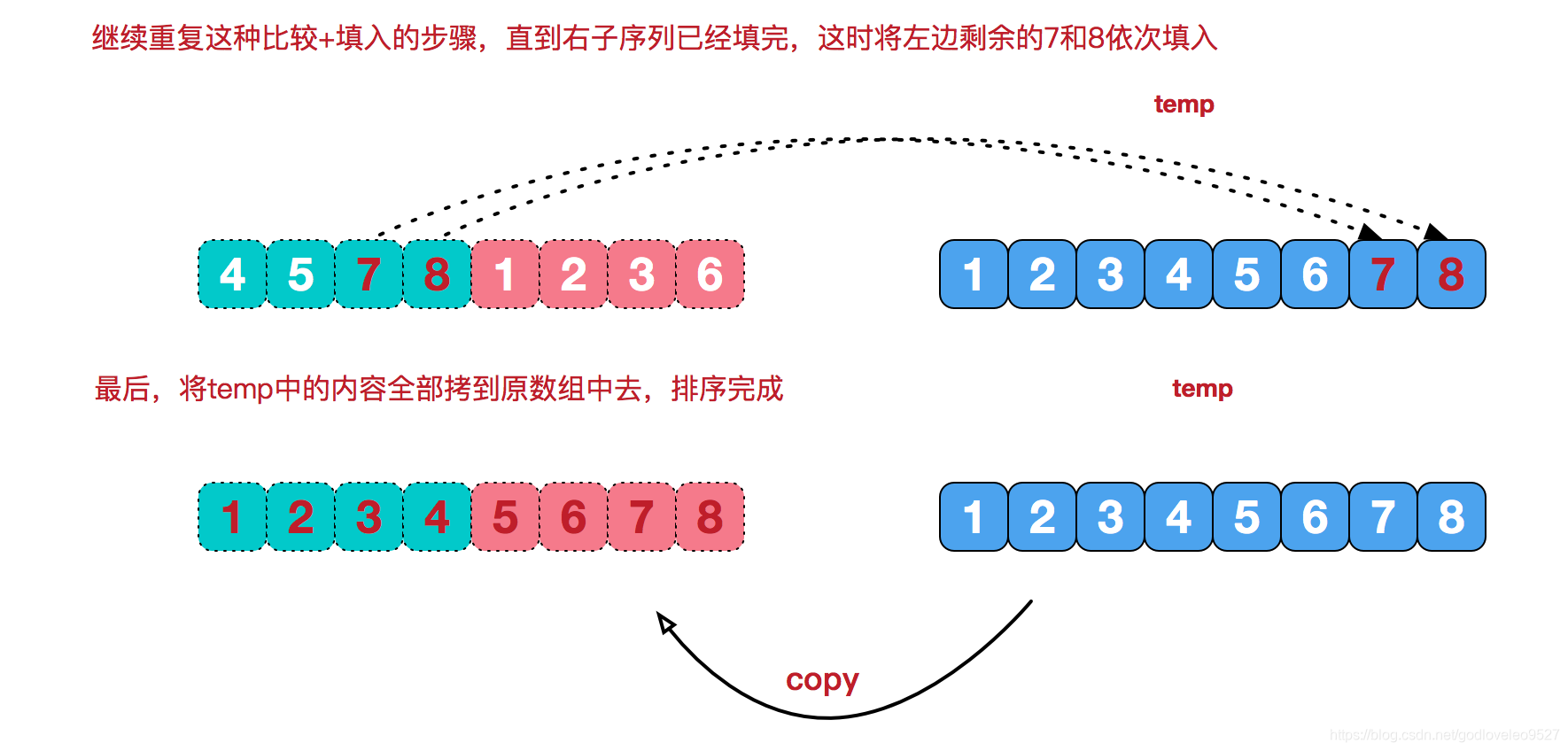
2.代码实现

public static void mergeSort(int[] array) {
    int[] temp = new int[array.length];// 在排序前，先建好一个长度等于原数组长度的临时数组，避免递归中频繁开辟空间
    mergeSort(array, 0, array.length-1, temp);
    System.out.println(Arrays.toString(array));
}

private static void mergeSort(int[] arr, int left, int right, int []temp) {
    if(left < right) {
        int mid = (left+right) / 2;
        mergeSort(arr, left, mid, temp);// 左边归并排序，使得左子序列有序
        mergeSort(arr, mid+1, right, temp);// 右边归并排序，使得右子序列有序
        merge(arr, left, mid, right, temp);// 将两个有序子数组合并操作
    }
}

private static void merge(int[] arr, int left, int mid, int right, int[] temp) {
    int i = left;// 左序列指针
    int j = mid+1;// 右序列指针
    int t = 0;// 临时数组指针
    while (i <= mid && j <= right) {
        if(arr[i] <= arr[j]) {
            temp[t++] = arr[i++];
        } else {
            temp[t++] = arr[j++];
        }
    }
    while(i <= mid) {// 将左边剩余元素填充进temp中
        temp[t++] = arr[i++];
    }
    while(j <= right) {// 将右序列剩余元素填充进temp中
        temp[t++] = arr[j++];
    }
    t = 0;
    // 将temp中的元素全部拷贝到原数组中
    while(left <= right) {
        arr[left++] = temp[t++];
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

3.时间复杂度和空间复杂度

归并排序是稳定排序，它也是一种十分高效的排序，能利用完全二叉树特性的排序一般性能都不会太差。java中Arrays.sort()采用了一种名为TimSort的排序算法，就是归并排序的优化版本。从上文的图中可看出，每次合并操作的平均时间复杂度为O(n)，而完全二叉树的深度为|log2n|。总的平均时间复杂度为O(nlogn)。而且，归并排序的最好，最坏，平均时间复杂度均为O(nlogn)。

八、基数排序

1.基本思路

• 1.基数排序的思想就是先排好各位，然后排好各位的基础上排十位，以此类推，直到遍历最高位 次，排序结束（仔细理解最后一句话）
• 2.基数排序不是比较排序，而是通过分配和收集的过程来实现排序
• 3.初始化10个桶(固定的)，桶下标为0-9
• 4.通过得到待排序数字的个十百等位的数字，把这个数字对应的item放到对应的桶中
• 5.基数排序有两种排序方式：LSD和MSD，最小位优先(从右边开始)和最大位优先(从左边开始)

2.代码实现

public static void radixSort(int[] array) {
    ArrayList<ArrayList<Integer>> queue = new ArrayList<>();
    for (int i = 0; i <10 ; i++) {
        queue.add(new ArrayList<>());// 创建一个基数从0---9 每个数字上都是一个list
    }
    // 找到最大值，并判断最大值是几位数
    int max = array[0];
    for (int i = 1; i < array.length; i++) {
        if (max < array[i]) {
            max = array[i];
        }
    }
    int time = 0;
    while (max > 0) {
        max /= 10;
        time++;
    }
    for (int i = 0; i < time; i++) {// 循环每一个位数（个位、十位、百位）
        for (int j = 0; j < array.length; j++) {// 循环数组，取每一个值
            int x = array[j] % (int) Math.pow(10, i + 1) / (int) Math.pow(10, i);
            ArrayList<Integer> queue3 = queue.get(x);

            queue3.add(array[j]);
            queue.set(x, queue3);
        }
        int count = 0;
        for (int k = 0; k < 10; k++) {
            while (queue.get(k).size() > 0) {
                ArrayList<Integer> queue4 = queue.get(k);
                array[count] = queue4.get(0);
                queue4.remove(0);
                count++;
            }
        }
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

3.时间复杂度和空间复杂度

归并排序是稳定排序，它也是一种十分高效的排序，能利用完全二叉树特性的排序一般性能都不会太差。java中Arrays.sort()采用了一种名为TimSort的排序算法，就是归并排序的优化版本。从上文的图中可看出，每次合并操作的平均时间复杂度为O(n)，而完全二叉树的深度为|log2n|。总的平均时间复杂度为O(nlogn)。而且，归并排序的最好，最坏，平均时间复杂度均为O(nlogn)。

总结

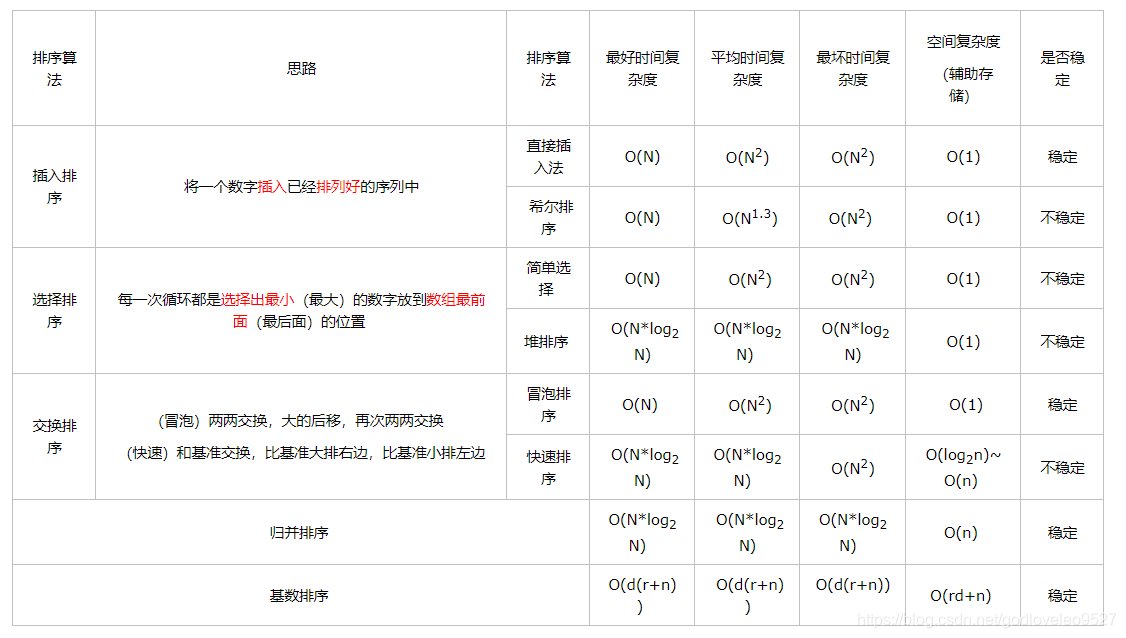
引用：

https://www.cnblogs.com/mensan/p/10570050.html

https://www.cnblogs.com/jyroy/p/11248691.html

https://www.cnblogs.com/chengxiao/p/6194356.html

https://www.jianshu.com/p/8340dfaea3af