超通俗理解注意力机制的原理与本质——结合日常生活来理解_注意力机制说不清楚

最近在学习nlp，看了好久Transformer的attention model，总结了一个贴近生活的理解。

论文的核心公式

Q：query（查询）
K： key（键）
V： value（值）
论文中的核心公式与上述三个主要参数有关，那么该怎么理解这个公式呢

从淘宝购买出发

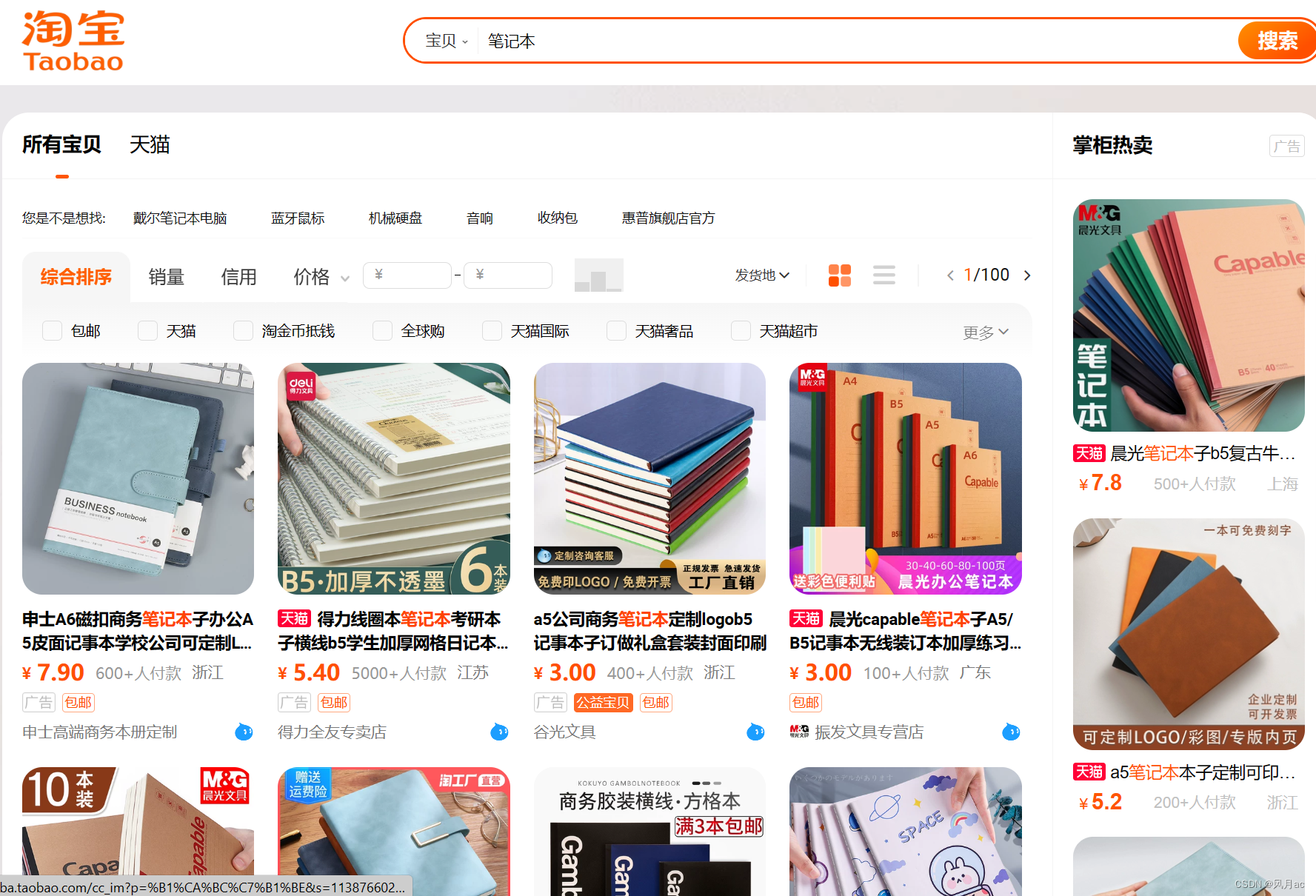
在淘宝的搜索栏中输入关键字“笔记本”，淘宝会跳出各种笔记本，其中一个个的排序就类似于“注意力”，淘宝希望我们把注意力放在它推荐的前几个“笔记本”中，这排名就类似于带权重的价值。

从购买笔记本的例子到对应公式

1、【查询】

我们输入查询(query，Q)，比如"笔记本”

2、【计算相似性】

淘宝后台拿到这个查询Q，并用这个查询Q去和后台的所有的商品的关键字(或者title)(key, K)一一的来对比，找到物品和我们查询的相似性(或者说物品对应的相似性的权重)，相似性越高，越可能推送给我们

3、【得到价值】

并且这个时候还要考虑物品的价值（(value，V)，这个V不是指物品值几块钱，而是这个物品在算法中的价值。如果商家给了淘宝广告钱，或者商品物美价廉，评论好，点赞高，购买多，等等，那么算法就越有可能把物品排在前面推送给我们。

4、【计算带权重的价值】

我们拿刚刚的相似性，乘上物品在算法中的价
值V，计算结果就是每件物品的最后的带相似性权重的价值，淘宝最后的算法就是返回这个带权重的价值，也就是把排好序的这些商品推送给我们。

5、【总结】

这就是一个最典型的注意力的过程。它推送在最前面给我们的商品，肯定就是它最希望获得我们注意力的商品。当然，淘宝内部的算法肯定不是这样的，但是他们的本质都是一样的，都是基于注意力，并且我们看到的现象也都是一样的。

公式中提到的dk是什么？

原文是这么描述的：对于较小的dk值，两种机制的性能相似，加性注意优于乘积注意，而不对d的较大值进行缩放；我们怀疑，对于dk的更大值，点积变大，将Softmax函数推到具有极小梯度的区域。为了抵消这种影响，我们缩放了刻度到1/根号下dk。
个人理解核心就是为了消除梯度变小、学习速度变慢的问题

计算过程和实现

输入编码

首先通过Word2Vec等词嵌入方法将输入语料转化成特征向量，论文中使用的词嵌入的维度为 d=512 。

在最底层的block中， x 将直接作为Transformer的输入，而在其他层中，输入则是上一个block的输出。为了画图更简单，我们使用更简单的例子来表示接下来的过程，如图所示：

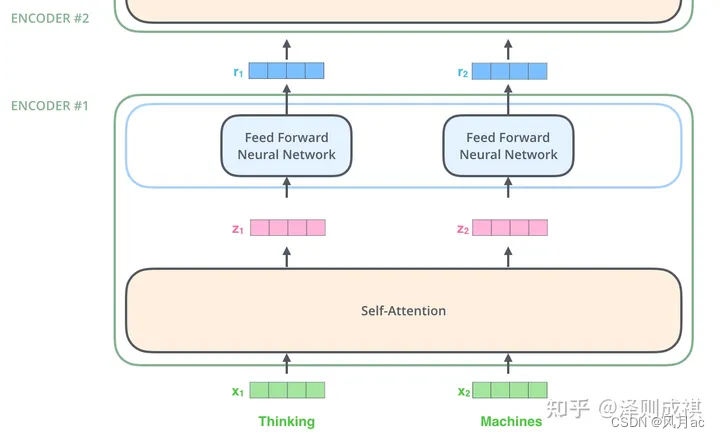
其中的核心就是：自注意力，Self-Attention是Transformer最核心的内容，其核心内容是为输入向量的每个单词学习一个权重，例如在下面的例子中我们判断it代指的内容，

The animal didn't cross the street because it was too tired
1

通过加权之后可以得到类似下图的加权情况：

在self-attention中，每个单词有3个不同的向量，它们分别是Query向量（Q），Key向量（K）和Value向量（V），长度均是64。它们是通过3个不同的权值矩阵由嵌入向量X，乘以三个不同的权值矩阵 Wq，Wk，Wv 得到，其中三个矩阵的尺寸也是相同的。均是 512×64。这个矩阵是随机初始化的，其值在BP的过程中会一直进行更新。

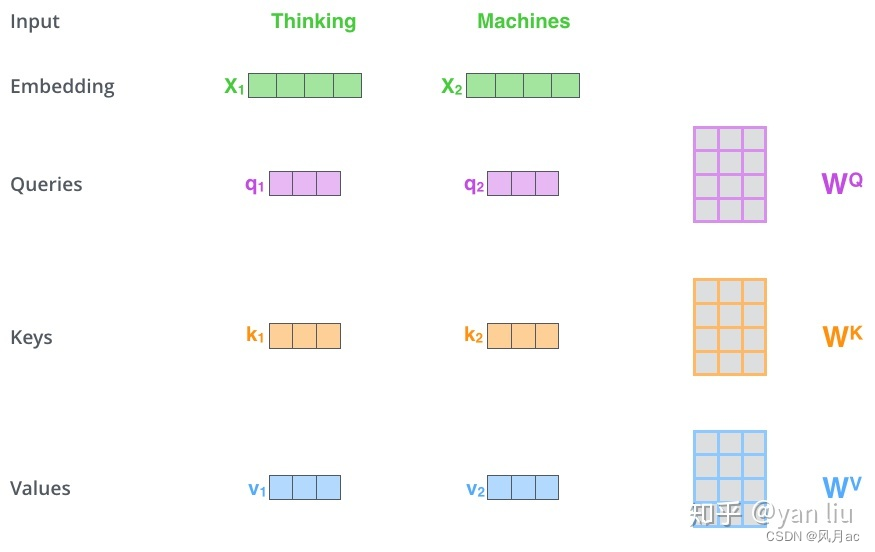
以thinking、machines为例，先转换为词嵌入向量，再根据权值矩阵 Wq，Wk，Wv 得到各自的Q，K，V，再结合上面的具体实例，得到各自的得分和带权重的价值。

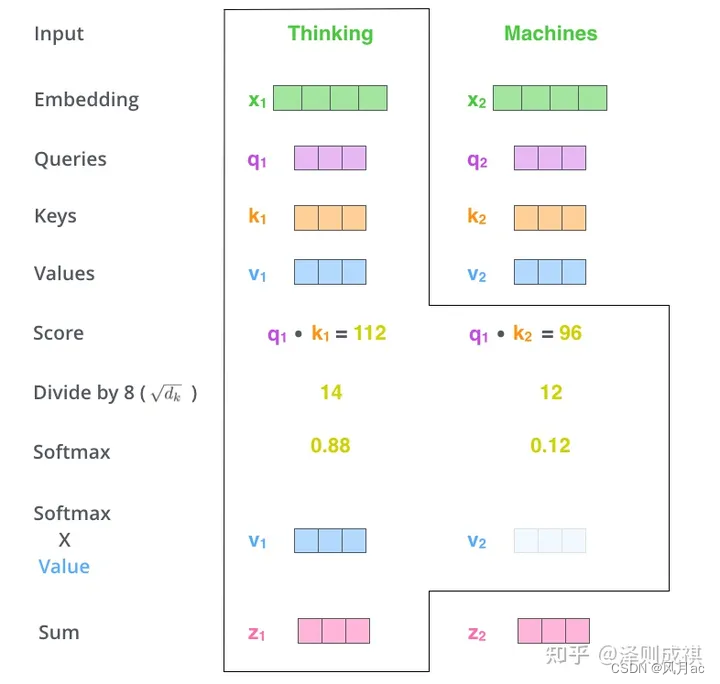
这也就实现了淘宝中查询的key，对应搜索得到列表中所有排列出来的商品，列表中的每一个商品都是查询title的相似性的权重乘商品所带的价值Value，对应就是softmax权重乘上V1得到z1，最后再进行一个组合，相当于把所有商品堆在一起给出一个列表。
总结：Q, K, V 的计算
Attention 的输入用矩阵 X 进行表示，则可以使用线性变阵矩阵 WQ, WK, WV 计算得到 Q, K, V。计算如下图所示，注意 X, Q, K, V 的每一行都表示一个单词。最终我们可以用矩阵的形式取计算Q,K,V

代码：transformer代码

self-attention总结

详细步骤详解如下：
1. 输入句子
2. self-attention会计算出三个新的向量，在论文中，向量的维度是512维，我们把这三个向量分别称为Query、Key、Value，这三个向量是用embedding向量与一个矩阵相乘得到的结果，这个矩阵是随机初始化的，维度为（64，512）注意第二个维度需要和embedding的维度一样，其值在BP的过程中会一直进行更新，得到的这三个向量的维度是64。
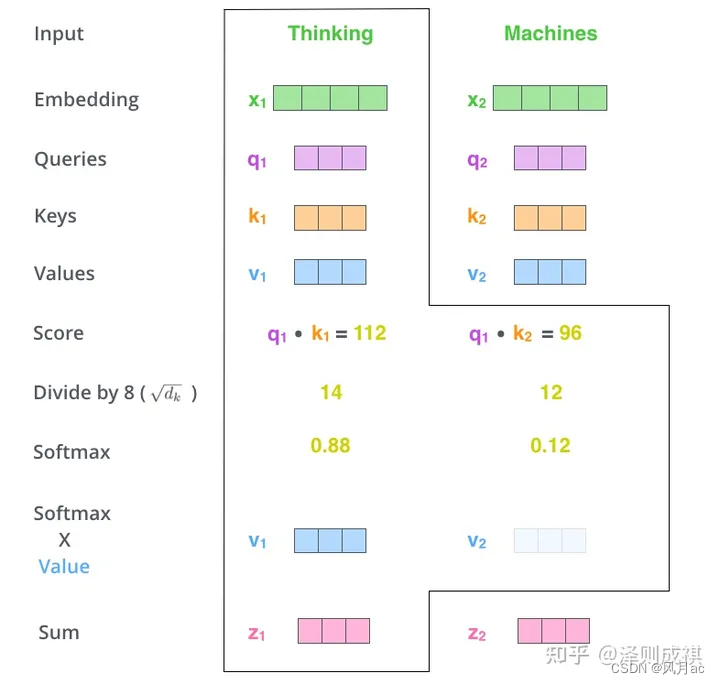
3. 计算self-attention的分数值，该分数值决定了当我们在某个位置encode一个词时，对输入句子的其他部分的关注程度。这个分数值的计算方法是Query与Key做点乘。首先我们需要针对Thinking这个词，计算出其他词对于该词的一个分数值，首先是针对于自己本身即q1·k1，然后是针对于第二个词即q1·k2。
4.5. 接下来，把点成的结果除以一个常数，这里我们除以8，这个值一般是采用上文提到的矩阵的第一个维度的开方即64的开方8，当然也可以选择其他的值，然后把得到的结果做一个softmax的计算。得到的结果即是每个词对于当前位置的词的相关性大小，当然，当前位置的词相关性肯定会会很大。
**6.**下一步就是把Value和softmax得到的值进行相乘，并相加，得到的结果即是self-attetion在当前节点的值。

举例理解

以中文翻译成英文为例子时，可以将中文作为查询（query）。我们以中文翻译成英文的任务为例，假设我们有一个中文句子作为输入：“我喜欢学习深度学习”。

首先，将输入的中文句子中的每个词（“我”、“喜欢”、“学习”、“深度学习”）通过嵌入层转换为向量表示。这些向量表示将作为自注意力机制的输入。
假设经过嵌入层后，得到以下词嵌入向量：

"我" -> [0.7, 0.9, 0.2]
"喜欢" -> [0.3, 0.6, 0.8]
"学习" -> [0.1, 0.6, 0.8]
"深度学习" -> [0.7, 0.9, 0.2]
1
2
3
4

接下来，我们将这些向量表示使用线性变换矩阵 $W_q$、$W_k$ 和 $W_v$，转换为查询（query）、键（key）和值（value）向量。假设这些变换后的向量为：

查询 (q) = [0.5, 0.3, 0.2]
键 (k) = [0.1, 0.6, 0.8]
值 (v) = [0.7, 0.9, 0.2]
1
2
3

现在，我们使用这些查询、键和值向量来计算自注意力分数和注意力权重。

假设我们的模型想要强调输入中的第一个词 “我”，那么它会计算每个词与 “我” 的相关性，得到注意力权重：

注意力权重：[0.8, 0.2, 0.3, 0.1]
1

接着，根据注意力权重，我们将值向量加权求和，得到最终的注意力输出：

注意力输出：(0.8 * [0.7, 0.9, 0.2]) + (0.2 * [0.3, 0.6, 0.8]) + (0.3 * [0.1, 0.6, 0.8]) + (0.1 * [0.7, 0.9, 0.2]) = [0.59, 0.78, 0.41]
1

最后，这个注意力输出会被用来辅助模型进行中文到英文的翻译，帮助模型决定如何最好地将"我喜欢学习深度学习"翻译成英文。

总之，中文句子作为查询（query）通过自注意力机制得到相关的键（key）和值（value）信息，然后计算注意力权重，最后通过加权求和得到注意力输出，以帮助模型在翻译任务中更好地关注与当前查询相关的信息。

加入代码理解

在自注意力机制中，涉及到三个线性变换矩阵，通常用符号 $W_q$、$W_k$、$W_v$ 来表示。这些矩阵是模型的可学习参数，它们是通过在训练过程中进行学习来得到的。

假设我们有一个输入句子，其中包含多个单词或标记。每个单词或标记都会经过一个嵌入层（embedding layer），得到一个向量表示，作为自注意力机制的输入。

现在，我们来看看这三个矩阵是怎么用的，并通过一个类比来解释它们的作用：
$W_q$ (Query Matrix):
$W_q$用于将输入向量转换为一个“查询”向量，即用来寻找与输入中每个位置相关的信息。你可以将$W_q$看作是一个“寻找相关信息”的工具。

$W_k$ (Key Matrix):
$W_k$用于将输入向量转换为一个“键”向量，即用来确定不同位置之间的相关性。你可以将$W_k$看作是一个“确定相关性”的工具。

$W_v$ (Value Matrix):
$W_v$用于将输入向量转换为一个“值”向量，即用来提供每个位置的具体信息。你可以将$W_v$看作是一个“提供具体信息”的工具。

举个例子来说明：
假设我们有一个输入句子： “ChatGPT is an amazing language model.”

我们首先将每个单词嵌入为向量表示：

"ChatGPT" -> [0.2, 0.7, 0.1]
"is" -> [0.3, 0.5, 0.2]
"an" -> [0.1, 0.4, 0.5]
"amazing" -> [0.9, 0.3, 0.6]
"language" -> [0.5, 0.8, 0.4]
"model" -> [0.6, 0.2, 0.9]
1
2
3
4
5
6

接下来，我们使用三个线性变换矩阵：$W_q$、$W_k$和$W_v$，将这些向量转换为查询、键和值向量：

Query (q) = [0.5, 0.2, 0.3]
Key (k) = [0.1, 0.6, 0.8]
Value (v) = [0.7, 0.9, 0.2]
1
2
3

现在，我们可以使用这些查询、键和值向量来计算自注意力分数和注意力权重。
假设我们的模型想要强调输入句子中的第一个单词 “ChatGPT”，那么它会计算每个单词与 “ChatGPT” 的相关性，得到注意力权重：

Attention scores: [0.8, 0.2, 0.3, 0.1, 0.4, 0.5]
1

接着，根据注意力权重，我们将值向量加权求和，得到最终的注意力输出：

Attention output = (0.8 * [0.7, 0.9, 0.2]) + (0.2 * [0.3, 0.5, 0.2]) + (0.3 * [0.1, 0.4, 0.5]) + (0.1 * [0.9, 0.3, 0.6]) + (0.4 * [0.5, 0.8, 0.4]) + (0.5 * [0.6, 0.2, 0.9])
                 = [0.63, 0.62, 0.38]
1
2

在这个例子中，通过使用$W_q$、$W_k$和$W_v$矩阵，模型能够找到与查询向量（来自输入句子的"ChatGPT"）相关的键和值，从而计算出最终的注意力输出。这使得模型能够在自注意力机制中更好地关注与当前查询相关的信息，从而更好地理解输入序列的结构和语义。

三个权重参数问题

对于Transformer中的注意力机制，包括三个线性变换矩阵 $W_q$、$W_k$ 和 $W_v$，它们都是模型的可学习参数，是在训练过程中通过反向传播算法来优化得到的。

在训练阶段，模型通过大量的数据进行学习，不断地调整这些参数，以使得模型在完成特定任务（如机器翻译）时表现最佳。

这三个矩阵是通过随机初始化的，也就是说，在模型开始训练时，它们的值是随机选择的。初始时，模型并不知道如何最好地使用这些矩阵，因此训练过程就是通过与真实标签进行比较，逐渐调整这些参数，使得模型能够在给定输入下得到更好的输出。

输入并不直接决定这些矩阵的初始值。它们的初始化是在模型设计中指定的，通常遵循一定的标准初始化方法，例如从均匀分布或高斯分布中随机抽样。

需要强调的是，这些矩阵是共享的，也就是说，在自注意力机制的不同位置（多个单词或标记）上，这些矩阵是相同的。这使得模型能够在不同位置共享参数，从而减少了需要学习的参数数量，提高了模型的训练效率和泛化能力。

总结起来，$W_q$、$W_k$ 和 $W_v$ 矩阵是Transformer模型的可学习参数，在训练过程中通过与真实标签的比较进行优化，使得模型能够自动学习并逐渐调整这些参数，以在给定输入下更好地进行自注意力计算。输入并不直接决定这些矩阵的初始值，而是通过训练来优化它们，使得模型能够在特定任务上表现最佳。

注意力机制和自注意力机制的差距

注意力机制（Attention Mechanism）和自注意力机制（Self-Attention Mechanism）实际上是同一种基本机制的不同应用。

注意力机制（Attention Mechanism）

在注意力机制中，我们有两个不同的输入序列，通常称为“查询序列”（Query Sequence）和“键值序列”（Key-Value Sequence）。查询序列用来确定我们要关注的位置或信息。键值序列是我们希望查询序列关注的对象。注意力机制根据查询序列与键序列之间的相似度计算注意力权重，并根据这些权重对值序列进行加权求和，得到最终的注意力输出。

自注意力机制（Self-Attention Mechanism）：

自注意力机制是注意力机制的特殊情况，其中查询序列、键序列和值序列都来自于同一个输入序列。在自注意力机制中，输入序列中的每个位置都充当查询、键和值的角色，通过与其他位置计算注意力，来捕捉序列内部的依赖关系和重要信息。自注意力机制通过学习每个位置与其他位置之间的相对重要性，从而计算出最终的自注意力输出。

示例：

假设我们有一个输入序列：["I", "love", "AI", "and", "NLP"]。
1

注意力机制示例：

查询序列为 "love"。
键值序列为 ["I", "AI", "and", "NLP"]。
1
2

注意力机制根据查询序列与键序列的相似度计算注意力权重，并对值序列进行加权求和，得到关于 “love” 的注意力输出。

自注意力机制示例：

在自注意力机制中，我们将输入序列 ["I", "love", "AI", "and", "NLP"] 
视为同时充当查询、键和值的序列。
1
2

自注意力机制计算每个位置与其他位置之间的相对重要性，并对输入序列进行加权求和，得到序列内部的自注意力输出。

总结：

注意力机制是一种更一般的机制，它可以用于许多任务，包括自然语言处理中的机器翻译等。而自注意力机制则是注意力机制的特殊形式，用于处理同一个序列内部的信息交互和建模。在Transformer等模型中，自注意力机制被广泛应用，用于学习输入序列中不同位置的依赖关系，从而提高模型的表现。

参考

[1]: 作者：范仁义-AI编程 出处：bilibili
[2]: 《Attention Is All You Need》，Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, Illia Polosukhin
[3]: 大师兄的深度学习笔记
[4]: 台湾大学李宏毅机器学习

理解注意力机制的一些好文章

[1] Transformer详解笔记-知乎
[2] Attention Models
[3] 台湾大学李宏毅机器学习-blbl
[4] 全网最透彻的注意力机制的通俗原理与本质【推荐】