数学建模 （线性规划 python代码 两种)_线性规划怎么编程

线性规划： 

线性规划（Linear Programming，LP）是一种数学优化方法，用于解决一类特定类型的最优化问题。该问题的目标是在给定的一组线性约束条件下，找到使某个线性目标函数达到最大或最小的变量值。线性规划问题可以表示为以下标准形式：

最小化（或最大化）：Z = c^T * x

约束条件：Ax <= b, x >= 0

其中，c是一个n维向量，表示线性目标函数的系数；x是一个n维向量，表示待求解的变量；A是一个m×n的矩阵，表示约束条件的系数；b是一个m维向量，表示约束条件的右侧常数。

线性规划问题的解可以通过以下步骤求得：

1. 将问题转化为标准形式。
2. 判断是否存在可行解，即是否存在满足所有约束条件的变量值。
3. 利用线性规划算法求解最优解。常用的线性规划算法包括单纯形法、内点法等。
4. 检验最优解的可行性和稳定性。
5. 根据实际问题对最优解进行解释和应用。

线性规划广泛应用于经济学、工程学、运筹学等领域，用于解决资源分配、生产计划、货运调度等问题。

运用scipy.optimize：

求最大值：

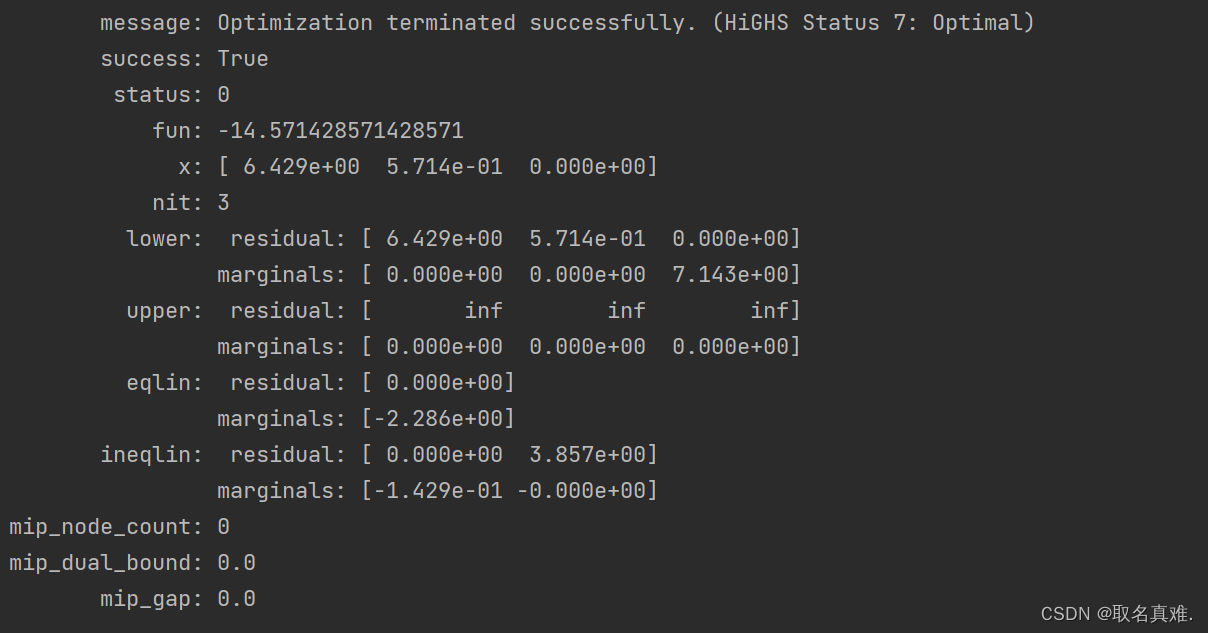
import numpy as np
c = np.array([2,3,-5])#目标函数系数
 
A = np.array([[-2,5,-1],[1,3,1]])#不等式<=左侧未知数系数矩阵
B = np.array([-10,12])#不等式<=右侧未知数系数矩阵
 
Aeq = np.array([[1,1,1]])#等式左侧系数矩阵
Beq = np.array([7])#等式右侧系数矩阵
 
x1 = [0, None]  #未知数取值范围
x2 = [0, None]  #未知数取值范围
x3 = [0, None]  #未知数取值范围
 
res = optimize.linprog(-c,A,B,Aeq,Beq,bounds=(x1, x2, x3))#求最大值，将目标函数系数转为负数，求最小值（即为最大值）
print(res)
 
#最大值即为14

 求最小值：

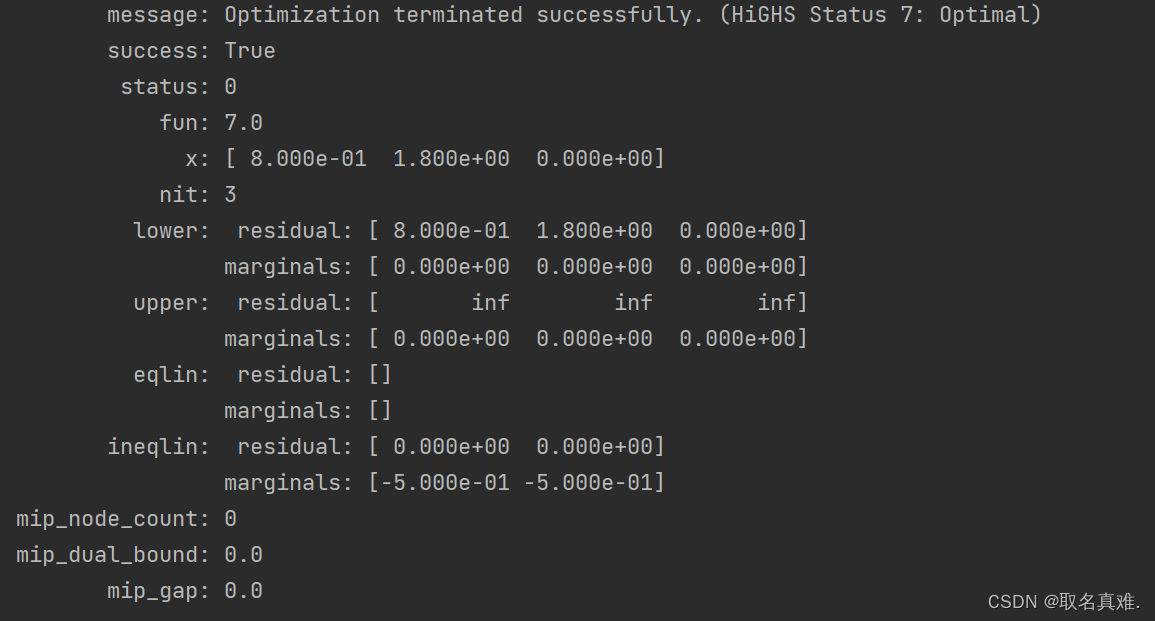
#coding=gbk
from scipy import optimize
import numpy as np
c = np.array([2,3,1])#目标函数系数
 
A = np.array([[-1,-4,-2],[-3,-2,0]])#不等式<=左侧未知数系数矩阵
B = np.array([-8,-6])#不等式<=右侧未知数系数矩阵
 
x1 = [0, None]  #未知数取值范围
x2 = [0, None]  #未知数取值范围
x3 = [0, None]  #未知数取值范围
res = optimize.linprog(c,A,B,bounds=(x1, x2, x3))
print(res)
 
#最小值为7

运用cvxpy库：

求最大值：

import cvxpy as cp
from numpy import array
 
c = array([70, 50, 60])  #定义目标向量
a = array([[2, 4, 3], [3, 1, 5], [7, 3, 5]])  #定义约束矩阵
b = array([150, 160, 200])  #定义约束条件的右边向量
x = cp.Variable(3, pos=True)  #定义3个决策变量
obj = cp.Maximize(c@x)    #构造目标函数
cons = [a@x <=b]     #构造约束条件
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')   #求解问题
print('最优解为：', x.value)
print('最优值为：', prob.value)

求最小值：

import cvxpy as cp
 
x=cp.Variable((4,4),pos=True)
obj=cp.Minimize(2800*sum(x[:,0])+4500*sum(x[:3,1])+
    6000*sum(x[:2,2])+7300*x[0,3])
cons=[sum(x[0,:])>=15,
      sum(x[0,1:])+sum(x[2,:3])>=10,
      sum(x[0,2:])+sum(x[1,1:3])+sum(x[2,:2])>=20,
      x[0,3]+x[1,2]+x[2,1]+[3,0]>=12]
prob=cp.Problem(obj,cons)
prob.solve(solver='GLPK_MI')
print("最优值为：",prob.value)
print("最优解为：\n",x.value)