吴恩达深度学习笔记：超 参 数 调 试 、 Batch 正 则 化 和 程 序 框 架（Hyperparameter tuning）3.8-3.9

第二门课: 改善深层神经网络：超参数调试、正 则 化 以 及 优 化 (Improving Deep Neural Networks:Hyperparameter tuning, Regularization and Optimization)

第三周： 超 参 数 调 试 、 Batch 正 则 化 和 程 序 框 架（Hyperparameter tuning）

3.8 Softmax 回归（Softmax regression）

到目前为止，我们讲到过的分类的例子都使用了二分分类，这种分类只有两种可能的标记 0 或 1，这是一只猫或者不是一只猫，如果我们有多种可能的类型的话呢？有一种 logistic回归的一般形式，叫做 Softmax 回归，能让你在试图识别某一分类时做出预测，或者说是多种分类中的一个，不只是识别两个分类，我们来一起看一下。

假设你不单需要识别猫，而是想识别猫，狗和小鸡，我把猫加做类 1，狗为类 2，小鸡是类 3，如果不属于以上任何一类，就分到“其它”或者说“以上均不符合”这一类，我把它叫做类 0。这里显示的图片及其对应的分类就是一个例子，这幅图片上是一只小鸡，所以是类3，猫是类 1，狗是类 2，我猜这是一只考拉，所以以上均不符合，那就是类 0，下一个类 3，以此类推。我们将会用符号表示，我会用大写的C来表示你的输入会被分入的类别总个数，在这个例子中，我们有 4 种可能的类别，包括“其它”或“以上均不符合”这一类。当有 4 个分类时，就是 0、1、2、3。

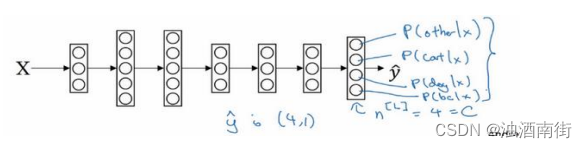
在这个例子中，我们将建立一个神经网络，其输出层有 4 个，或者说C个输出单元，因此n，即输出层也就是L层的单元数量，等于 4，或者一般而言等于C。我们想要输出层单元的数字告诉我们这 4 种类型中每个的概率有多大，所以这里的第一个节点(最后输出的第 1个方格+圆圈)输出的应该是或者说我们希望它输出“其它”类的概率。在输入X的情况下，这个(最后输出的第 2 个方格+圆圈)会输出猫的概率。在输入X的情况下，这个会输出狗的概率(最后输出的第 3 个方格+圆圈)。在输入X的情况下，输出小鸡的概率（最后输出的第 4 个方格+圆圈），我把小鸡缩写为 bc（baby chick）。因此这里的$\hat{y}$将是一个4 × 1维向量，因为它必须输出四个数字，给你这四种概率，因为它们加起来应该等于 1，输出中的四个数字加起来应该等于 1。

让你的网络做到这一点的标准模型要用到 Softmax 层，以及输出层来生成输出，让我把式子写下来，然后回过头来，就会对 Softmax 的作用有一点感觉了。

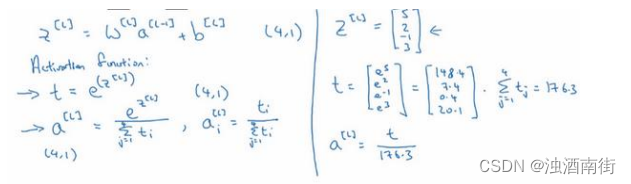
在神经网络的最后一层，你将会像往常一样计算各层的线性部分，$z^{[l]}$这是最后一层的z变量，记住这是大写L层，和往常一样，计算方法是$z^{[l]}=W^{[l]}{a}^{[L-1]}+b^{[l]}$，算出了