空间复杂度与链表刷题

"一切的一切都是你自己在感应."

前言:
本文主要探究空间复杂度与链表题目讲解
更多文章点击主页: 酷酷学!!!
如果此文对您有帮助, 您的点赞与关注是我最大的动力 !

---

正文开始

空间复杂度

空间复杂度也是一个数学表达式, 是对一个算法在运行时临时占用存储空间大小的量度.
空间复杂度不是程序占用了多少bytes的空间, 因为这个也没太大意义, 所以空间复杂度算的是变量的个数. 空间复杂度计算规则基本跟时间复杂度类似, 也使用大O渐进表示法.
注意: 函数运行时所需要的栈空间(存储参数,局部变量,一些寄存器信息等)在编译期间已经确定好了, 因此空间复杂度主要通过函数在运行时候显示申请的额外空间来确定.

复杂度实例

实例1

// 计算BubbleSort的空间复杂度？
void BubbleSort(int* a, int n)
{
    assert(a);
    for (size_t end = n; end > 0; --end)
    {
        int exchange = 0;
        for (size_t i = 1; i < end; ++i)
        {
            if (a[i - 1] > a[i])
            {
                Swap(&a[i - 1], &a[i]);
                exchange = 1;
            }
        }

        if (exchange == 0)
            break;
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

解析:

首先解决这个问题我们需要计算额外的空间, 这里一共创建了三个变量, end, exchange, i ,使用了常数个额外空间，所以空间复杂度为 O(1)

实例2

// 计算Fibonacci的空间复杂度？
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{
    if (n == 0)
        return NULL;

    long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));
    fibArray[0] = 0;
    fibArray[1] = 1;
    for (int i = 2; i <= n; ++i)
    {
        fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
    }

    return fibArray;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

解析:

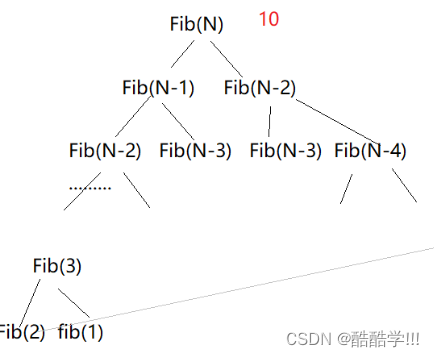
这里,一共开辟了N个函数栈帧, 动态开辟了N个空间，空间复杂度为 O(N),而时间复杂度为O(2^N).

实例3

// 计算阶乘递归Fac的空间复杂度？
long long Fac(size_t N)
{
    if (N == 0)
        return 1;

    return Fac(N - 1) * N;
}
1
2
3
4
5
6
7
8

解析:

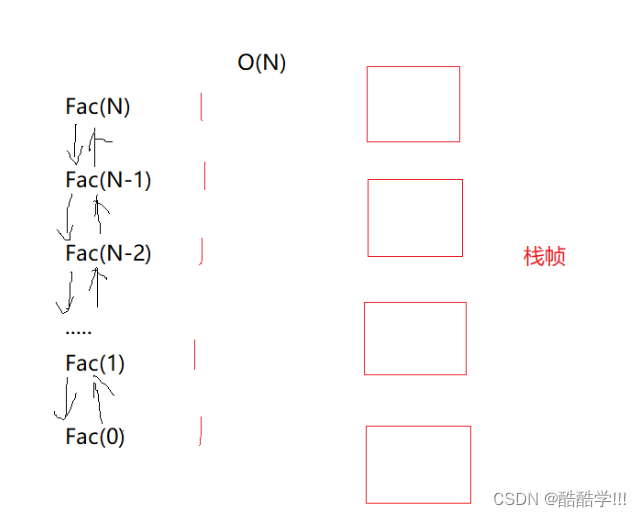
递归调用了N次，开辟了N个栈帧，每个栈帧使用了常数个空间。空间复杂度为O(N)

链表题目

1. 返回倒数第K个节点

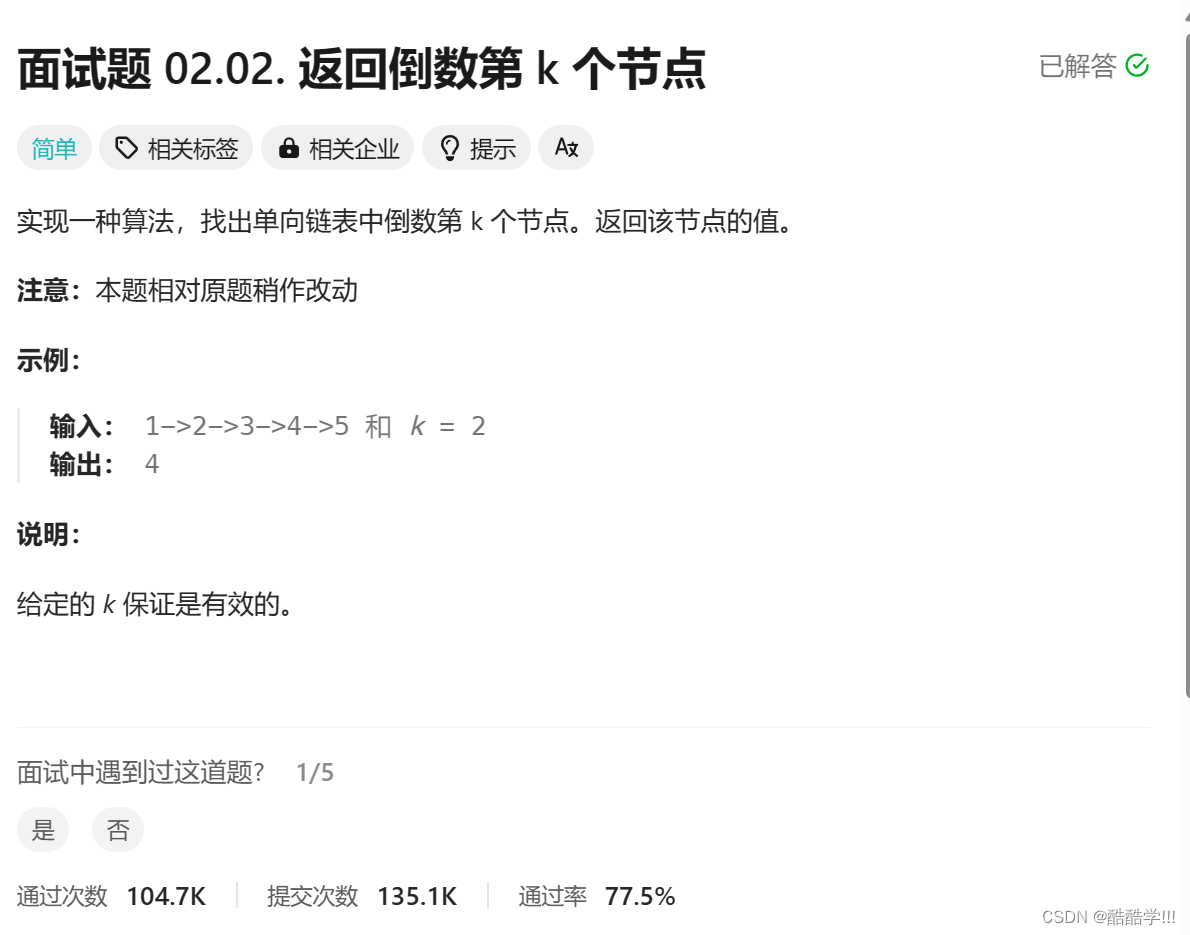
题目链接: 返回倒数第K个节点

题目描述:

题目分析:
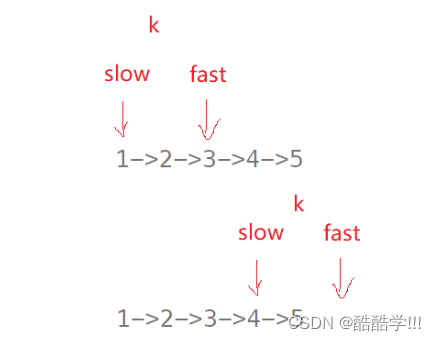
       本题的解法有很多种, 例如创建数组, 或者将链表反转等等, 这里我们采用一种比较经典的双指针法, 只需要变量一遍链表, 并且空间复杂度为O(1),时间复杂度为O(N), 首先采用数理思想, 定义快慢指针, 快指针先走K个节点,然后在同时走, 因为中间的差距一直为K,所以当快指针走到NULL的时候, 此时慢指针即为倒数第K个节点.因为题目要求K值是有效的, 所以我们也无需判断K值是否有效.

画图演示:

代码如下:

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */

//时间复杂度为O(1)
int kthToLast(struct ListNode* head, int k){

    struct ListNode* fast = head;
    struct ListNode* slow = head;

    while(k--)
    {
        fast = fast->next;
    }
    while(fast)
    {
        fast = fast->next;
        slow = slow->next;
    }
    return slow->val;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

2. 链表的回文结构

题目链接: 链表的回文结构

题目描述:

题目分析:

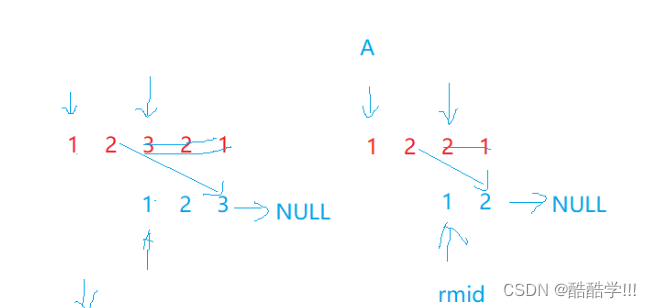
       本题可以说是一个综合题, 结合前面对链表的掌握, 理解了思路就变得比较简单, 首先回文结构并不陌生, 数组题目中我们已经见过, 例如12321, 或者1221就是回文结构, 如果是数组, 我们可以采用双指针法, 一个在头, 一个在尾, 两两比较, 分别向中间前进, 但是此时是个链表, 该如何比较呢.

       单链表链表的结构不能直接从后向前遍历, 首先第一步, 寻找中间节点, 然后将中间节点之后的链表进行反转, 然后从头结点开始与中间节点之后的链表的值进行比较, 当然我们需要讨论链表为奇数或者偶数的情况, 但是不难发现, 如下图所示, 不管是奇数还是偶数, 都不影响, 我们只需要判断其中一个链表是否走到NULL.

画图演示:

代码如下:

/*
struct ListNode {
    int val;
    struct ListNode *next;
    ListNode(int x) : val(x), next(NULL) {}
};*/
#include <cstddef>
class PalindromeList {
public:
        
    //1. 寻找中间节点
    struct ListNode * midNode(ListNode* A)
    {
        struct ListNode * fast = A;
        struct ListNode * slow = A;
        while(fast&&fast->next)
        {
            fast = fast->next->next;
            slow = slow->next;
        }
        return slow;
    }
    //2.反转后半段链表
    struct ListNode *reverseNode(ListNode* mid)
    {
        if(mid == NULL)
        {
            return mid;
        }
        struct ListNode * l1 = NULL;
        struct ListNode * l2 = mid;
        struct ListNode * l3 = mid->next;
        while(l2)
        {
            l2->next = l1;
            l1 = l2;
            l2 = l3;
            if(l3)
            {
                l3 = l3->next;
            }
        }
        return l1;
    }

    bool chkPalindrome(ListNode* A) {
        struct ListNode * mid = midNode(A);
        struct ListNode * B = reverseNode(mid);
        while(A&&B)
        {
            if(A->val != B->val)
            {
                return false;
            }
            A = A->next;
            B = B->next;
        }
        return true;
        // write code here
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61

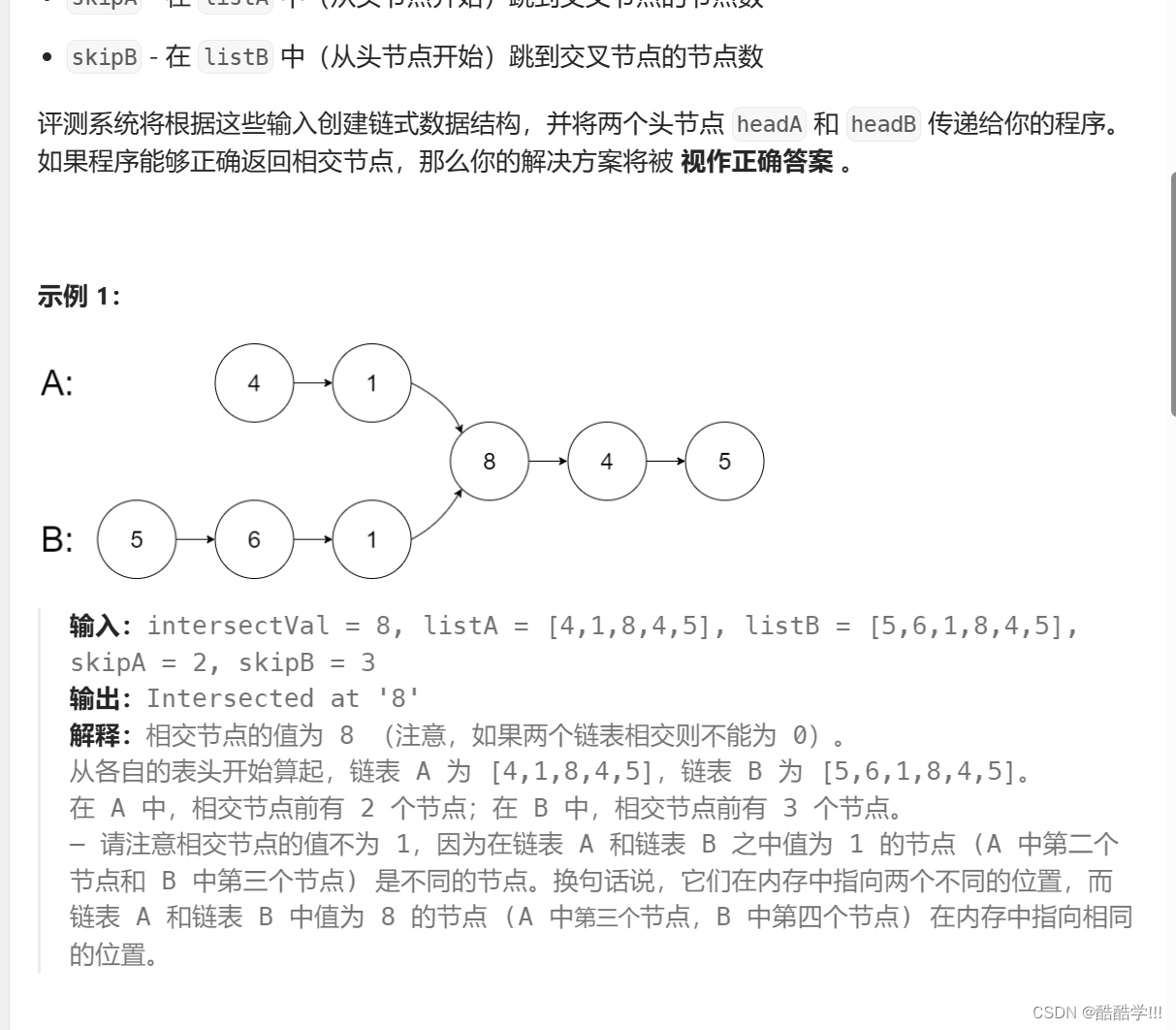
3. 相交链表

题目链接: 相交链表

题目描述:

题目分析:

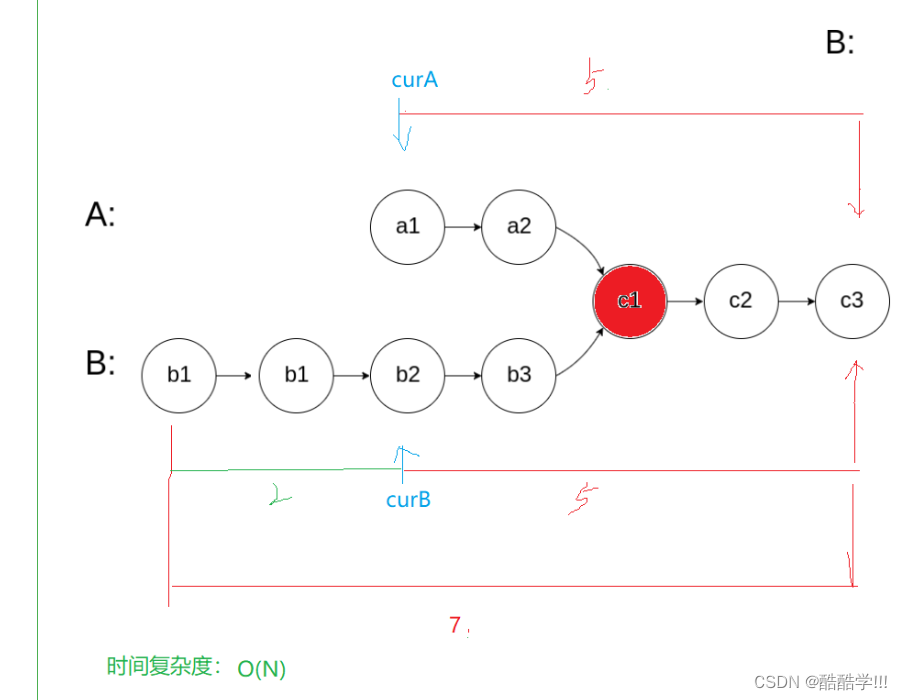
       判断链表相交, 如果说一个一个比较的话, 链表A的节点依次和链表B的节点一次进行比较这样太麻烦了, 而且时间复杂度为O(N^2), 那么, 判断链表相交 ,我们可以遍历链表, 如果两个链表最后一个节点相等的话, 那么就一定相交, 但是如何返回第一个相交节点呢, 通过分别比较吗, 大可不必, 在我们遍历链表的时候, 我们可以顺便计算出链表的相对差值, 然后让长的链表走差值的距离, 在同时走, 那么只要两个节点相遇, 就是第一个相交节点.

画图演示:

代码如下:

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
    struct ListNode* cur1 = headA;
    struct ListNode* cur2 = headB;
    int long1 = 0,long2 = 0;
    while(cur1->next)
    {
        long1++;
        cur1 = cur1->next;
    }
    while(cur2->next)
    {
        long2++;
        cur2 = cur2->next;
    }
    if(cur1 != cur2)
    {
        return NULL;
    }
    struct ListNode* LongList = headA;
    struct ListNode* ShortList = headB;
    if(long2>long1)
    {
        LongList = headB;
        ShortList = headA;
    }
    int dig = abs(long1-long2);
    while(dig--)
    {
        LongList = LongList->next;
    }
    while(LongList!=ShortList)
    {
        LongList = LongList->next;
        ShortList = ShortList ->next;
    }
    return LongList;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

4. 随机链表的复制

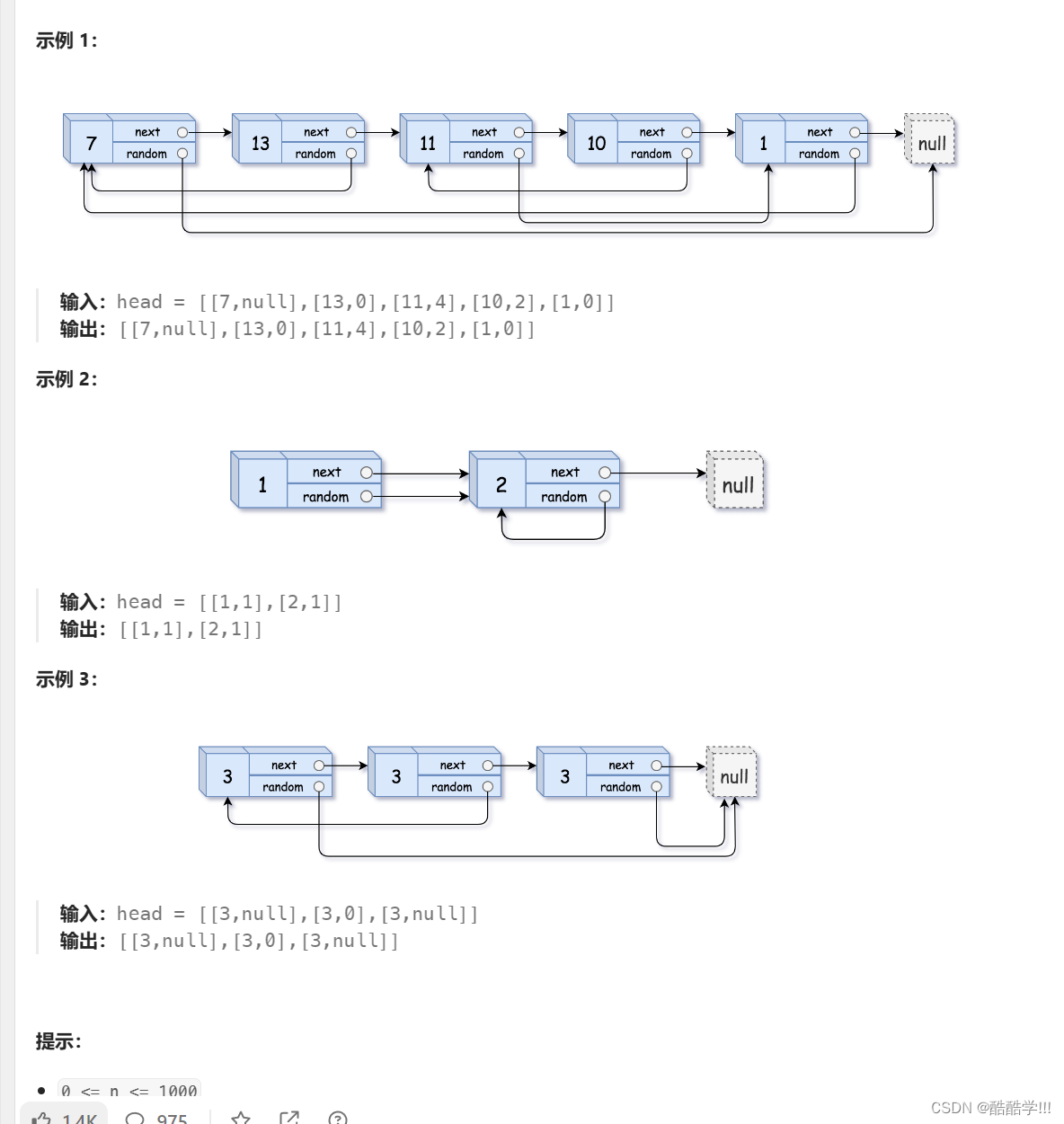
题目分析:
       深拷贝就是复制出来一个一模一样的链表, 如果我们直接创建一个新的节点, 但是对random的处理比较麻烦, 我们需要计算出相对位置, 以确保random的指向正确. 这里我们换一种思路, 如下图所示, 我们在每个节点之后插入一个新的节点, 此时处理random就比较简单了,拷贝节点的 random的指向就是cur->random->next. 最后再将拷贝节点拿下来尾插, 成为一个新的链表.虽然破坏了原链表的结构, 我们也可以进行恢复, 但是题目没有要求 ,所以, 我们也可以不用恢复.

画图演示:

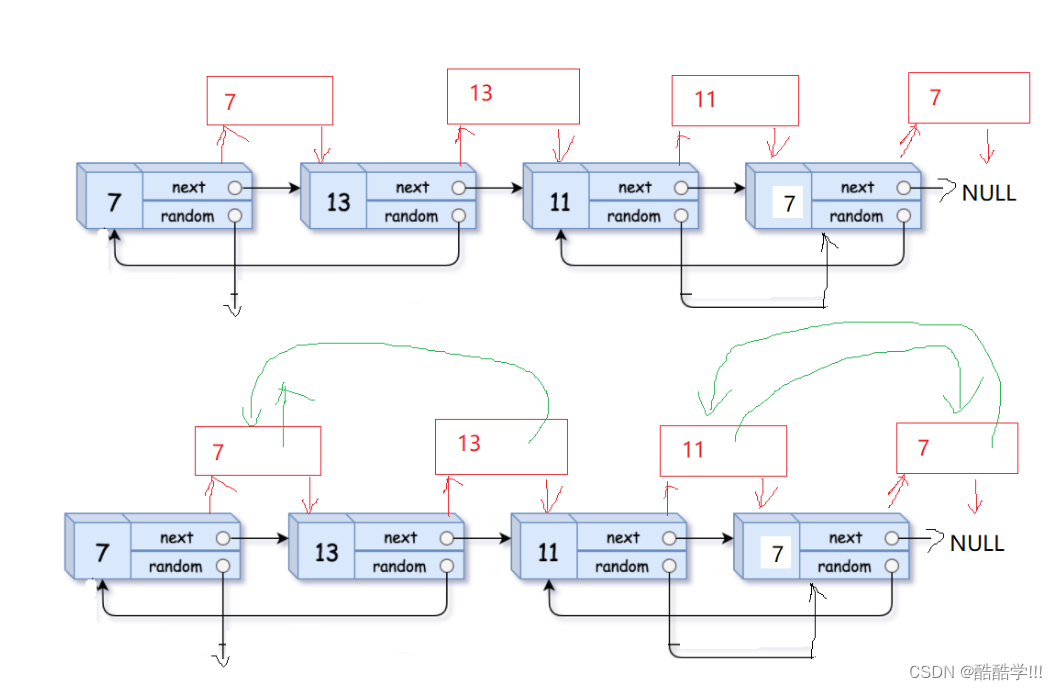
代码如下:

/**
 * Definition for a Node.
 * struct Node {
 *     int val;
 *     struct Node *next;
 *     struct Node *random;
 * };
 */

struct Node* copyRandomList(struct Node* head) {
    struct Node* cur = head;
	while(cur)
    {
        struct Node* copyNode = (struct Node*)malloc(sizeof(struct Node));
        copyNode->val = cur->val;
        copyNode->next = cur->next;
        cur->next = copyNode;
        cur = copyNode->next;
    }
    cur = head;
    while(cur)
    {   
        struct Node* copy = cur->next;
        if(cur->random == NULL)
        {
            copy->random = NULL;
        }
        else
        {
            copy->random = cur->random->next;
        }
        cur = copy->next;
    }
    cur = head;
    struct Node* copyHead = NULL;
    struct Node* copyTail = NULL;
    while(cur)
    {
        struct Node* copy = cur->next;
        //Node* next = copy->next;
        if(copyTail == NULL)
        {
            copyHead = copyTail = copy;
        }
        else
        {
            copyTail->next = copy;
            copyTail = copyTail->next;
        }
        cur = copy->next;
        //cur = next;恢复原链表
    }
    return copyHead;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

5. 环形链表

题目链接:环形链表2

题目描述:

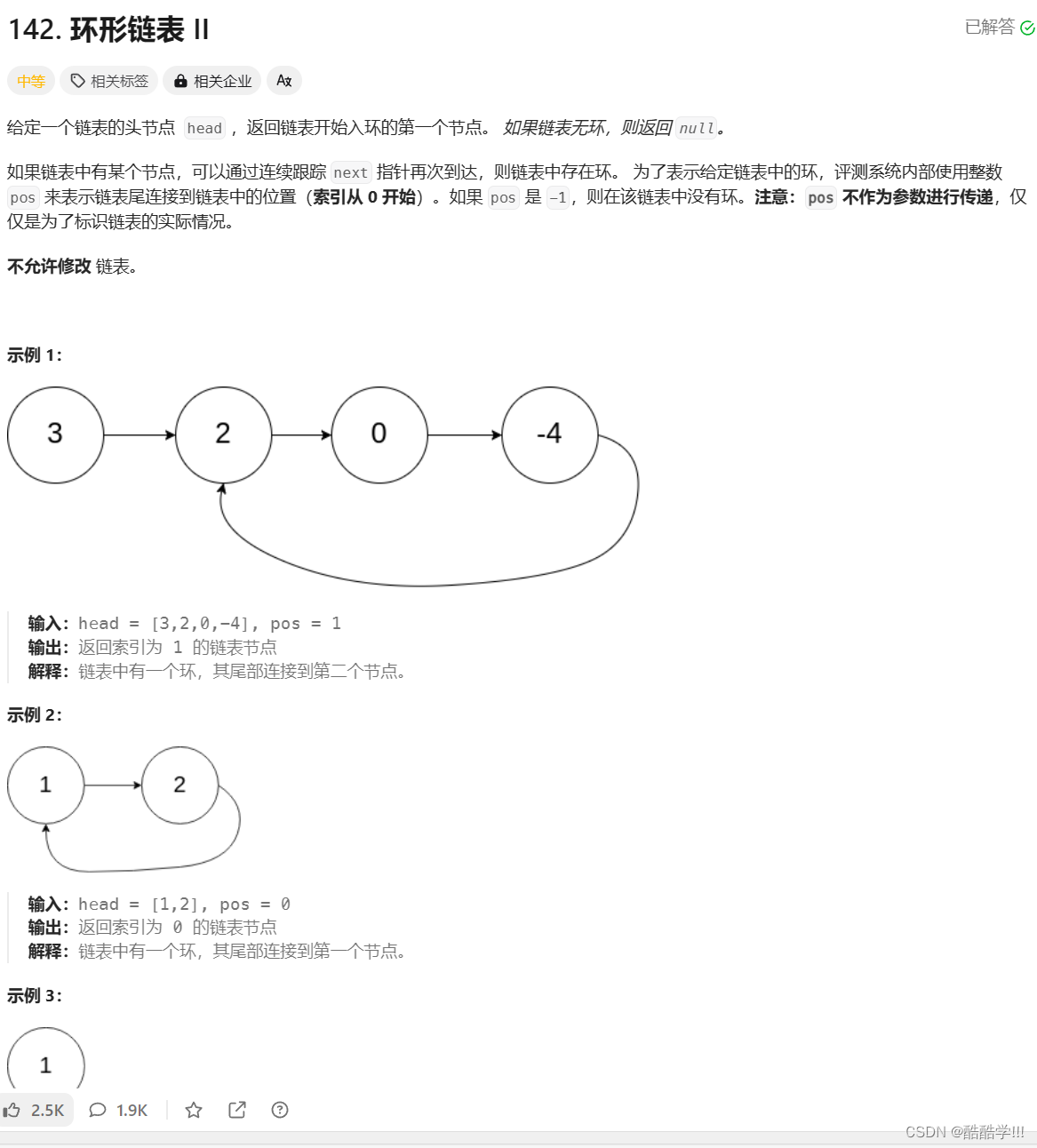
代码如下:

这里我们采用双指针法, 快指针一次走两步 , 慢指针一次走一步, 因为有相对速度, 所以当慢指针进入环时,快指针开始追击, 当快指针追击上满指针则带环, 若追击不上,则不带环.
面试时可能会问到:

1. 为什么一定会相遇,有没有可能会错过, 永远追不上? 请证明
2. slow一次走一步, fast走3步 4步 5步 一定能追上吗? 请证明

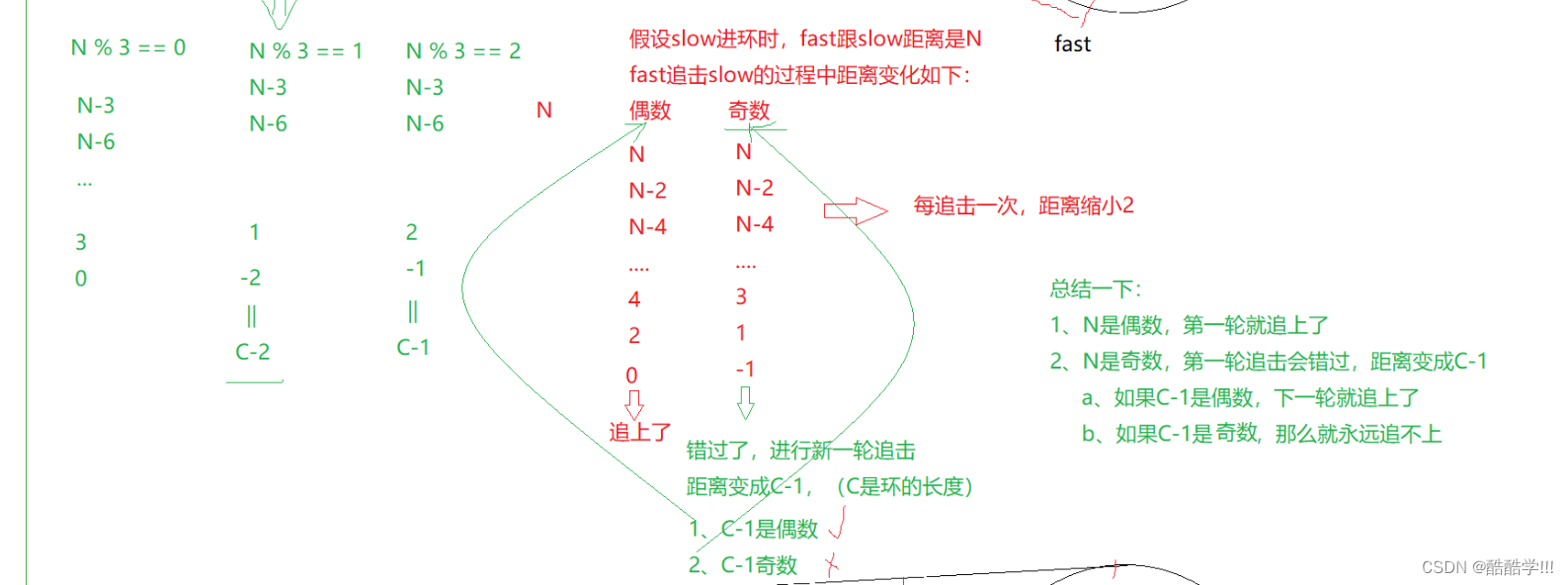
首先证明问题1, 一次走一步, 假设slow进环时, fast和slow的距离是N, 那么fast追击slow过程中变化距离如下, 每次追击一次, 距离就缩小1, 距离为0就追上了.

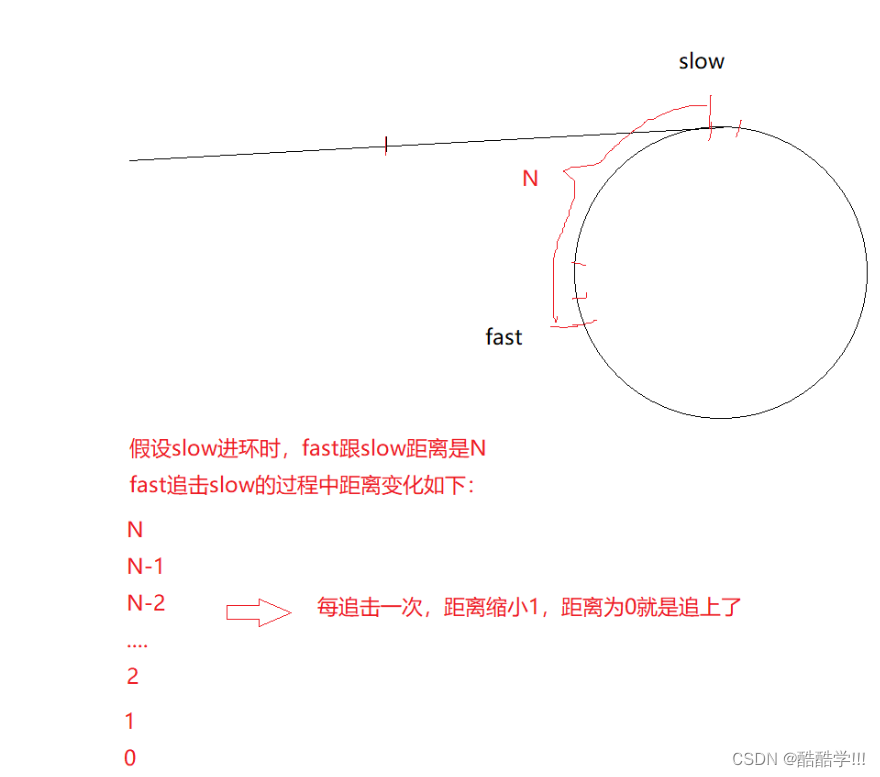
证明问题2:

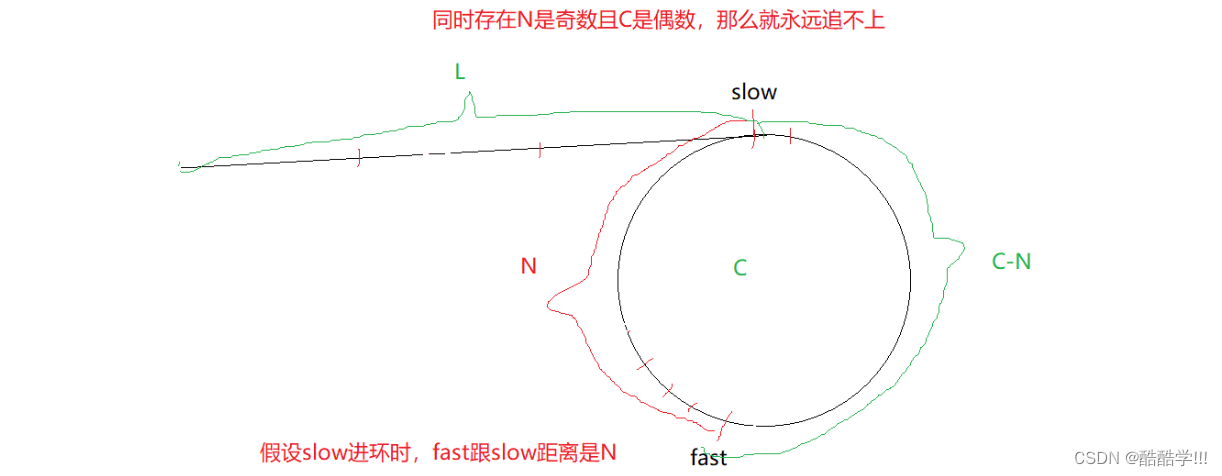
这里我们假设fast一次走3步, 当slow进环时, fast开始追击, 每次的距离变化如下, 如果N是偶数的情况下,那么就一定可以追上, 当为奇数时,就进入到第二次的追击, 假设环的长度为C, 那么下一次追击的距离就为C-1, 那如果C-1为偶数的话那么就可以追上, 但是如果C-1又为奇数那么就永远追不上, 此时我们就需要证明会不会永远追不上, 也就是证明当N为奇数的情况下, C-1为奇数, 即C为偶数吗, 通过fast走的距离和slow走的距离, 我们可以知道3slow = fast .

fast走的距离为:L + xC +C-N, (L为未进环时的长度, C为环的长度, x为走的圈数, N为slow进环时和fast的距离)
slow走的距离为: L
由此可得3L = L+XC+C-N
化简可以得到, 2L = (X+1)C - N
此时只需证明N为奇数, C能否为偶数, 是偶数就永远追不上
根据等式 2L一定为偶数, 而N假设为奇数, 那么C如果为偶数的话,
即 偶数 = (X+1)*偶数 - 奇数 等式不成立,
因为只有奇数-奇数才能等于偶数, 所以C 一定为奇数,故不可能追不上
其余证明思想类似

接下来, 我们判断出了是带环链表, 那我们如何找到入环时的第一个节点呢?

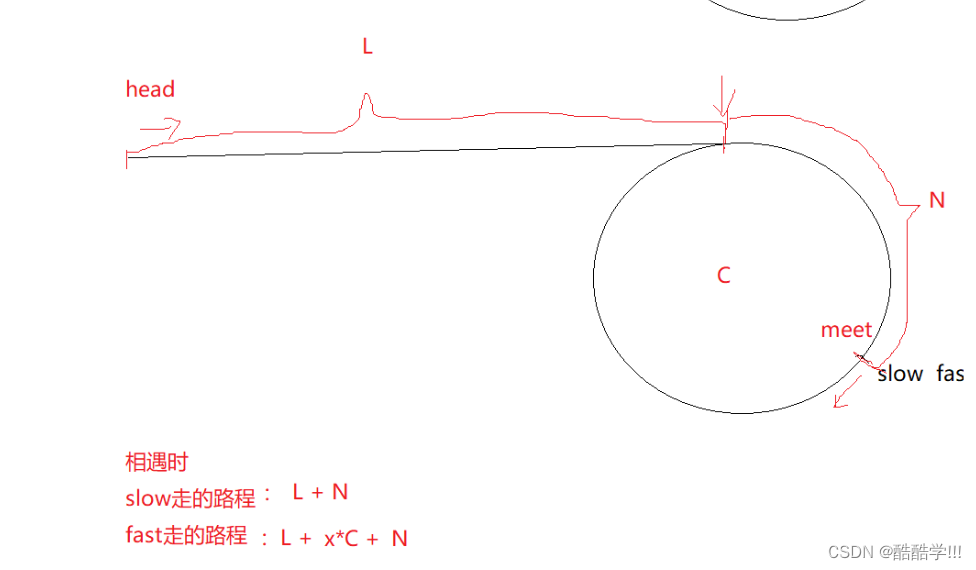
先来分析一波
假设相遇的时的节点为meet, 那么slow走的路程为L+N, fast走的路程为L+X * C +N ,根据2slow = fast,我们又可以得到
2(L+N) = L+X*C + N
化简得到
L+N = X *C
L = X *C-N
L = (X-1)C +C -N
(X-1)C可以想象成走了多少圈但是还是会回到meet那个位置, 所以L的到第一个入环节点的距离等于C-N
那么我们只需要随便找两个指针, 一个从head开始走, 一个从meet开始走, 只要他们两个相遇, 那么就是第一个入环节点.

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     struct ListNode *next;
 * };
 */
struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode* fast = head;
    struct ListNode* slow = head;
    while(fast&&fast->next)
    {
        fast = fast->next->next;
        slow = slow->next;
        if(fast==slow)
        {
            struct ListNode* meet = slow;
            fast = head;
            while(meet!=fast)
            {
            meet = meet->next;
            fast = fast->next;
            }
            return meet;
        }

    }
    return NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

---

总结:

空间复杂度表示算法在运行过程中需要使用的额外的空间资源。空间复杂度的计算通常是以算法需要的额外空间大小来衡量的。链表是一种常见的数据结构，用于存储和操作一系列具有关联关系的数据元素。
链表的面试题常见的有：
反转链表: 将一个链表反转，即将链表中的节点逆序排列。
链表中倒数第k个节点: 找到链表中倒数第k个节点的值。
链表是否有环: 判断一个链表是否存在环。
合并两个有序链表: 将两个有序链表合并为一个有序链表。
删除链表中的重复元素: 删除链表中重复的元素，使得每个元素只出现一次。
在解决链表面试题时，常用的方法有：
递归法: 使用递归的方式处理链表的问题，递归可以简化问题的处理过程。
快慢指针法: 使用快慢指针来寻找链表中的某个位置，如链表中的中间节点、倒数第k个节点等。
翻转链表法: 使用指针来改变链表节点的指向，实现链表的翻转。
在面试过程中，对于链表问题，需要注意空指针的处理，以及边界条件的判断。同时，对于链表的基本操作，如插入、删除等，也要熟练掌握。

最后感谢关注点赞, 如果错误欢迎指正.