不确定性推理——主观贝叶斯方法matlab实现_主观贝叶斯方式的不确定推理

一、实验名称

主观贝叶斯

二、实验目的

在证据不确定的情况下，根据充分性量度LS、必要性量度LN、E的先验概率P(E)和H的先验概率P(H)作为前提条件，分析P(H/S)和P(E/S)的关系。

三、实验原理及内容阐述

1、 证据不确定性的表示

1. 在主观Bayes方法中，证据的不确定性用概率表示。对于证据E，由用户根据观察S给出P(E|S)，即动态强度。用P(E|S)描述证据的不确定性 （证据E不是可以直接观测的）。
2. 证据肯定存在时，P(E|S)=1；
3. 证据肯定不存在时， P(E|S)=0；
4. 证据具有不确定性时， 0<P(E|S)<1。

2、LN和LS的意义

1. 当证据E愈是支持H为真时，则应是使相应的LS值愈大。若证据E对H愈是必要，则相应LN的值愈小。。
2. 不能出现LS>1且LN>1的取值
   因为： LS>1：表明证据E是对H有利的证据。
   LN>1：表明证据¬E是对H有利的证据。
3. 不能出现LS<1且LN<1的取值
   因为：LS<1: 表明证据 E是对H不利的证据。
   LN<1：表明证据¬E是对H不利的证据。
4. 一般情况下，取LS>1， LN<1。

3、证据不确定的情况

在现实中，证据肯定存在和肯定不存在的极端情况是不多的，更多的是介于二者之间的不确定情况。对初始证据来说，由于用户对客观事物或现象的观察不是很精确，因而所提供的证据是不确定的；另外，一条知识的证据往往来源于另一条知识推出的结论，一般也具有某种程度的不确定性。所以我们要在S对E的观察的先验概率0<P(E/S)<1的情况下确定H的后验概率P(H/S)。

在证据确定的情况下，我们因该用杜达等人1976年证明了的公式来进一步讨论：

分四种情况讨论这个公式：

1. P(E/S)=1
   当P(E/S)=1时，P(-E/S)=0。此时公式变成(肯定存在的情况)：

2. P(E/S)=0
   当P(E/S)=0时，P(-E/S)=1.此时公式变成(肯定不存在的情况)：

3. P(E/S)=P(E)
   当P(E/S)=P(E)时，表示E与S无关。利用全概率公式就将公式变为：

4. 当P(E/S)为其它值时，通过分段线性插值就可得到计算P(H/S)的公式：
   该公式称为EH公式或UED公式。

四、实验结果

输入：
PHE =0.8 ;
PH=0.6;
PH_E=0.2;
PE=0.25;
输出为

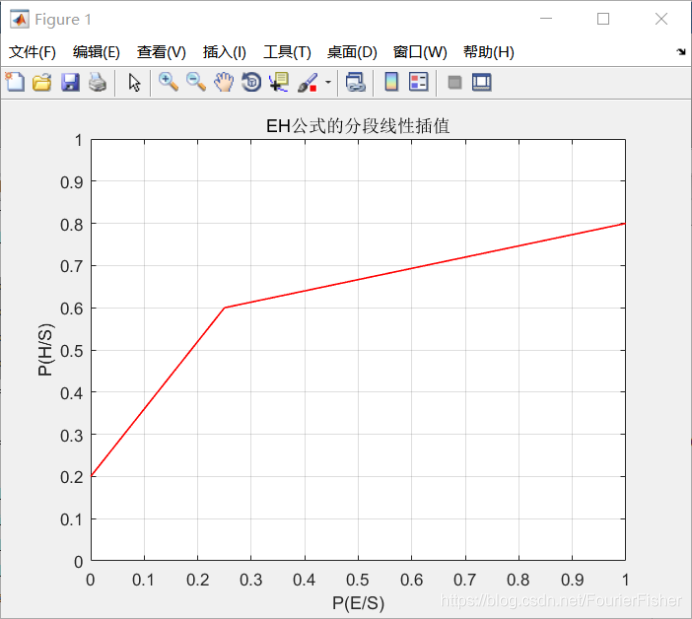
五、实验总结

通过实验，使我更加熟悉了主观Bayes方法的实质，根据先验概率的条件不同来分析后验概率，利用它们之间的关系，更好的了解不确定性推理方法。

六、附录

clc; clear all;

PHE =0.8 ;
PH=0.6;
PH_E=0.2;
PE=0.25;
x=0:0.001:1;
y=(((PH-PH_E)/PE)x+PH_E).(x>=0&x<PE)+((PHE-PH)/(1-PE)x+(PH-PHEPE)/(1-PE)).*(x>=PE&x<=1);

plot(x,y,‘r’,‘linewidth’,1)
title(‘EH公式的分段线性插值’)
xlabel(‘P(E/S)’)
ylabel(‘P(H/S)’)
axis([0 1 0 1])
grid on