模糊神经网络_开题答辩 模糊神经网络

FPGA教程目录

MATLAB教程目录

-----------------------------------------------------------------------

第一：隶属函数的设计

    隶属函数的设计，可以通过模糊编辑器，也可以通过如上的代码进行设计。

第二：模糊规则的设计

通过输入模糊规则量化表进行设计，所得到的模糊规则如下所示：

1. If (e is NB) and (ec is NB) then (u is PB) (1)

2. If (e is NB) and (ec is NM) then (u is PB) (1)

3. If (e is NB) and (ec is NS) then (u is PM) (1)

4. If (e is NB) and (ec is Z) then (u is PM) (1) 

5. If (e is NB) and (ec is PS) then (u is PS) (1)

6. If (e is NB) and (ec is PM) then (u is PS) (1)

7. If (e is NB) and (ec is PB) then (u is Z) (1) 

8. If (e is NM) and (ec is NB) then (u is PB) (1)

9. If (e is NM) and (ec is NM) then (u is PM) (1)

10. If (e is NM) and (ec is NS) then (u is PM) (1)

11. If (e is NM) and (ec is Z) then (u is PS) (1)

12. If (e is NM) and (ec is PS) then (u is PS) (1)

13. If (e is NM) and (ec is PM) then (u is Z) (1)

14. If (e is NM) and (ec is PB) then (u is NS) (1)

15. If (e is NS) and (ec is NB) then (u is PM) (1)

16. If (e is NS) and (ec is NM) then (u is PM) (1)

17. If (e is NS) and (ec is NS) then (u is PS) (1)

18. If (e is NS) and (ec is Z) then (u is PS) (1)

19. If (e is NS) and (ec is PS) then (u is Z) (1)

20. If (e is NS) and (ec is PM) then (u is NS) (1)

21. If (e is NS) and (ec is PB) then (u is NS) (1)

22. If (e is Z) and (ec is NB) then (u is PM) (1)

23. If (e is Z) and (ec is NM) then (u is PS) (1)

24. If (e is Z) and (ec is NS) then (u is PS) (1)

25. If (e is Z) and (ec is Z) then (u is Z) (1)  

26. If (e is Z) and (ec is PS) then (u is NS) (1)

27. If (e is Z) and (ec is PM) then (u is NS) (1)

28. If (e is Z) and (ec is PB) then (u is NM) (1)

29. If (e is PS) and (ec is NB) then (u is PS) (1)

30. If (e is PS) and (ec is NM) then (u is PS) (1)

31. If (e is PS) and (ec is NS) then (u is Z) (1)

32. If (e is PS) and (ec is Z) then (u is NS) (1)

33. If (e is PS) and (ec is PS) then (u is NS) (1)

34. If (e is PS) and (ec is PM) then (u is NM) (1)

35. If (e is PS) and (ec is PB) then (u is NM) (1)

36. If (e is PM) and (ec is NB) then (u is PS) (1)

37. If (e is PM) and (ec is NM) then (u is PS) (1)

38. If (e is PM) and (ec is NS) then (u is Z) (1)

39. If (e is PM) and (ec is Z) then (u is NS) (1)

40. If (e is PM) and (ec is PS) then (u is NM) (1)

41. If (e is PM) and (ec is PM) then (u is NM) (1)

42. If (e is PM) and (ec is PB) then (u is NB) (1)

43. If (e is PB) and (ec is NB) then (u is Z) (1)

44. If (e is PB) and (ec is NM) then (u is NS) (1)

45. If (e is PB) and (ec is NS) then (u is NS) (1)

46. If (e is PB) and (ec is Z) then (u is NM) (1)

47. If (e is PB) and (ec is PS) then (u is NM) (1)

48. If (e is PB) and (ec is PM) then (u is NB) (1)

49. If (e is PB) and (ec is PB) then (u is NB) (1)

第三：控制闭环的设计

通常，一个传统的模糊控制器的闭环结构如下所示：

模糊控制器的基本结构：

模糊控制效果图（模型一）：

模糊控制效果图（模型二）：

   隶属函数如下所示：

    这里重点介绍一下模糊神经网络控制器的设计，

第一：四层化神经网络层的结构设计：

第1层：

第2层：

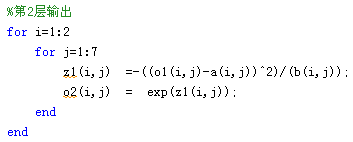
第3层：

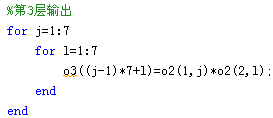
第4层：

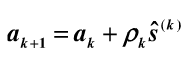
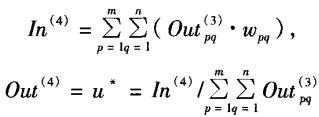
第二：利用梯度下降法进行权值更新

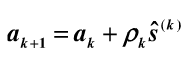
K聚类算法，常用的是K均值聚类算法，这里使用K均值聚类算法来实现。

·K-means聚类算法概述

K-means聚类算法基本思想，首先算法随机选取k个点作为初始聚类中心，然后计算各个数据对象到各聚类中心的距离，把数据对象归到离它最近的那个聚类中心所在的类；对调整后的新类计算新的聚类中心，如果相邻两次的聚类中心没有任何变化，说明数据对象调整结束，聚类准则Jc已经收敛。K-means聚类算法的一个特点是在每次迭代中都要考察每个样本的分类是否正确，若不正确，就要调整。在全部数据调整完后，再修改聚类中心，进入下一次迭代。如果在一次迭代算法中，所有的数据对象被正确分类，则不会有调整，聚类中心也不会有任何变化，这标志着Jc已经收敛，至此算法结束。本文重点对K-均值聚类算法进行了研究分析，并在K-均值聚类算法的基础上提出了改进。

·K-means聚类算法的基本原理

K-means聚类算法是硬聚类算法，是典型的基于原型的目标函数聚类分析算法点到原型——簇中心的某种距离和作为优化的目标函数，采用函数求极值的方法得到迭代运算的调整规则。K-means聚类算法以欧氏距离作为相异性测度它是求对应某一初始聚类中心向量最优分类，使得评价指标E值最小。

K-means聚类算法采用误差平方和准则函数作为聚类准则函数，误差平方和准则函数定义为：。其中为簇的数据对象，表示簇的均值。分析误差平方和准则函数可以看出E是样本与聚类中心差异度之和的函数，样本集X给定的情况下E的值取决于c个聚类中心。E描述n个样本聚类成c个类时所产生的总的误差平方和。显然，若E值越大，说明误差越大，聚类结果越不好。因此，我们应该寻求使E值最小的聚类结果，即误差平方和准则的最优结果。这种聚类通常称为最小误差划分。

误差平方和准则函数适用于各类样本比较集中而且样本数目悬殊不大的样本分布。当不同类型的样本数目相差较大时，采用误差平方和准则。很可能把样本数目多的类分开，以便达到总的误差平方和最小。

整个过程仿真结果如下所示：

中心和宽度的聚类结果：

两种方法的效果对比如下所示：

A05-06