- 1上海人工智能实验室的书生·浦语大模型学习笔记及作业--day5_上海人工智能实验室 大模型部署工具
- 2springboot集成mybatis-plus_mybatis-plus-boot-starter
- 3基于MISRA-C和VS Code的代码静态检查的开源解决方案_vscode 静态检查
- 4面试高频:什么是接口的幂等性,如何实现接口幂等性?_什么是幂等性?如何实现接口的幂等性。面试题
- 5web安全渗透测试工具篇(二):sqlmap常用命令和nmap常用命令_nmap和sqlmap
- 6git clone没有权限的解决方法_git没有权限clone代码
- 7Flutter 测试的最新进展
- 82024-1-22-数据结构作业
- 9nginx 交叉编译报错问题解决_checking for c compiler ... found but is not worki
- 10TCP/IP(网络编程)
【2023百度之星初赛】跑步,夏日漫步,糖果促销,第五维度,公园,新材料,星际航行,蛋糕划分_bd202311夏日漫步百度之星
赞
踩
目录
题目:跑步
小度每天早上要和小猫一起跑步。小猫的位置数值越小表示越在后面,速度越小表示越慢,它们都向一个方向跑。
小猫比较喜欢一起跑,所以当速度更快的小猫遇见速度慢的小猫时,它就会放慢速度,变成一组一起跑。注意,初始位置相同的小猫直接组成一组。
请问最终不再有追赶上的情况时,最多一组有多少只小猫?



思路:
我们先来捋一下题目哈:不同位置的小猫同时以不同速度开跑,当后面的猫追上前的猫时,它们就会以低速猫速度共速,成为一组,求最终一组最多的猫个数。
正着想不太好想,因为变化因素较多。我们可以倒着想:从最前面的猫开始推导,若i-1只猫速度大于第i只猫,不管i-1猫会不会被别的猫追上,都不会影响i-1猫追上i猫这个结果。然后要注意一下刚开始在同一位置的猫会直接分成一组。
操作:
我们先对猫按位置排列,同位置的猫猫速度小优先,然后先把同一位置的猫速度统一一下,此时同组的猫猫速度按最前面的猫速(最低速猫)设定速度,最后从后向前遍历:对i猫,将i后面连续所有v大于i的猫都直接统计出来(这个就是此组中最终会有的猫猫数),然后从i猫跳到不满足条件猫的位置(方便统计下一组的猫猫),不断重复即可!
- #include <bits/stdc++.h> //跑步:有n只小猫,出现在pi位置,速度为vi向前跑,不同速度小猫相遇时会共速成一组(取慢速那个),问最多一组的小猫个数
- using namespace std; //贪心,
- const int N=1e5+10;
- struct node{int p;int v;}ar[N];
- bool cmp(node x,node y){
- if(x.p!=y.p)return x.p<y.p;//必须这么写,可别偷懒!
- else return x.v<y.v;
- }
- int main(){
- int n;cin>>n;
- for(int i=1;i<=n;i++){
- scanf("%d%d",&ar[i].p,&ar[i].v);
- }
- sort(ar+1,ar+1+n,cmp);
- for(int i=1;i<n;i++){
- if(ar[i].p==ar[i+1].p) ar[i+1].v=ar[i].v;//同位置的猫速度给统一一下
- }
- int ans=-1,cnt=1,inde=n;//cnt来统计当前组有几只小猫
- while(1){
- if(inde-cnt==0)break;//遍历结束
- if((ar[inde].p!=ar[inde-cnt].p&&ar[inde].v<ar[inde-cnt].v)||(ar[inde].p==ar[inde-cnt].p))cnt++;
- //两个情况都要统计进去:两只猫位置不同但后猫更快, 两只猫位置相同
- else inde=inde-cnt,cnt=1;
- ans=max(ans,cnt);
- }
- cout<<ans;
- }

题目:夏日漫步
夏日夜晚,小度看着庭院中长长的走廊,萌发出想要在上面散步的欲望,小度注意到月光透过树荫落在地砖上,并且由于树荫的遮蔽度不通,所以月光的亮度不同,为了直观地看到每个格子的亮度,小度用了一些自然数来表示它们的亮度。亮度越高则数字越大,亮度相同的数字相同。
走廊是只有一行地砖的直走廊。上面一共有 n个格子,每个格子都被小度给予了一个数字 ai 来表示它的亮度。
小度现在站在 1号格子,想要去到 n号格子。小度可以正向或反向移动到相邻的格子,每次需要花费 1的体力。
同时小度还有瞬移的能力,其可以花费 1的体力来瞬移到与当前格子亮度相同的格子上。而且由于小度视野有限,只能瞬移到在当前格子后的第一次亮度相同的格子上。这也意味着不能反向瞬移。
小度想知道,到达 n号格子需要花费的最小体力是多少。以此制定一个最优秀的散步方案。


思路:
题意就是可以正向反向走一步,也能正向瞬移到相同亮度的地方。
这个题可以按照跑图题来做,每个相邻位置前后连起来,然后当前位置和之前同亮度位置单向连接,然后我们跑bfs,按步数进行遍历,就可以知道到最早哪一步时候可以走到终点!
- #include <bits/stdc++.h> //夏日漫步
- using namespace std;
- const int N=2e5;
- int pos[1000000];
- vector<int>v[N];
- queue<int>q;
- int main(){
- int len,ans=0,n,a;cin>>n;
- for(int i=1;i<=n;i++){
- scanf("%d",&a);
- if(i+1<=n)v[i].push_back(i+1),v[i+1].push_back(i);//正常建边
- if(!pos[a])pos[a]=i;
- else v[pos[a]].push_back(i),pos[a]=i;//正向瞬移建边
- }
- q.push(1);int p,sign=0;
- while(!q.empty()){
- ans++;//按层bfs
- len=q.size();
- while(len--){
- p=q.front();q.pop();
- for(int i=0;i<v[p].size();i++){
- if(v[p][i]==n){
- sign=1;break;}
- else if(p<v[p][i])q.push(v[p][i]);
- }
- if(sign)break;
- }
- if(sign)break;
- }
- cout<<ans;
- }

题目:糖果促销
小度最喜欢吃糖啦!!!
这天商店糖果促销,可给小度高兴坏了。
促销规则:一颗糖果有一张糖纸,p张糖纸可以换取一颗糖果。换出来糖果的包装纸当然也能再换糖果。
小度想吃 k颗糖果,他至少需要买多少颗糖?


思路:
注意到“至少 ”,细品!就是说最后一次换糖果时恰好没有多余的糖皮,即最终手里有一定且仅有一张糖皮(如果手里有大于两张糖皮的话,那就上次兑换就有多余的糖皮,也就是多买的糖)
好了,我们来分析:一共吃了k个糖,那么有k-1个糖皮被换成了糖,那么需要买的糖就是k-(k-1)/p;
最后呢!这个题其实还可以二分来做
- #include <bits/stdc++.h> //糖果促销:p个糖果可以换1个糖,想吃k个糖至少要买多少个糖 (1<=t<=1e6, 1<=p<=1e9, 0<=k<=1e9)
- using namespace std;
- int t,p,k;
- int main(){
- cin>>t;
- while(t--){
- cin>>p>>k;
- if(k==0) cout<<0<<'\n';//注意题上的数据范围
- else{
- k-=(k-1)/p;//一个式子就行
- cout<<k<<'\n';
- }
- }
- }
题目:第五维度
零维是点,点动成线;
一维是线,线动成面;
二维是面,面动成体;
三维是体,体动成史;
四维是史,史动????
现在人类企图理解第五维度。
而小度现在是第五维度的一位智者。一天,小度发现人类的许多科学家在试图理解第五维度,人类是四维生物,若是他们理解了第五维度,很可能也会到来第五维度的空间,这显然是小度不愿意看到的(毕竟哪里都有人口数量的问题….)所以小度希望他们尽可能晚的理解第五维度,因此,小度用更高维度的视角把所有人类中在理解第五维的科学家都看到了,而这些科学家的智商会不一样,所以他们的理解速度 Vi 也会不一样;并且,他们开始理解的时间点 Si 也不一样。理解速度 Vi 描述为每过单位时间可获得 Vi 个单位理解力,也就是说在 Si+1 的时间点该科学家会第一次贡献 Vi 的理解力。我们定义理解力总数超过 m 时理解了第五维度。 小度因为维度更高,可以使用时间悖论来给人类一次重大的打击,小度可以让任意一位科学家在任意一个时间点消失,所以他接下来的理解不会继续;而且人类不会记得他,所以他之前的贡献会消失。因为小度能力有限,所以小度只能使用一次暂时悖论。
现在求在尽可能晚的情况下,人类理解第五维度的最早时间点。
时间点初始为0,但显然,没有科学家能够在 0时刻有贡献。


思路:
二分答案,那么这次二分什么呢?当然是时间了!
我们只要遍历每个二分后的时间点就行,看在有效时间内贡献最多的人消失后还能不能理解第五维度,如果仍然可以理解,那么我们就继续减少时间,直到不能再减少时间,那么答案就出来了。
那么怎么知道最终的二分结果究竟能不能使人理解理解第五维度呢?我们只需要再带入一次check函数判断即可!
- #include <bits/stdc++.h>//第五维度:有n个科学家,在不同的时间点s出现,之后每天贡献v,当人类贡献总和大于m时,就理解了第五维度,但上帝可以随机
- using namespace std; //使一个人消失,他的所有贡献也会消失,问人类最晚多久可以理解第五维度,如果不能输出-1
- typedef long long ll;
- ll s[100000],v[100000],n,m;
- bool check(ll t){
- ll sum=0,max_=-1;
- for(int i=1;i<=n;i++){
- if(t<=s[i])continue;//后面出现的人就跳过
- sum+=(t-s[i])*v[i];
- max_=max(max_,(t-s[i])*v[i]);//找最大贡献的人
- }
- return sum-max_>m;
- }
- int main(){
- cin>>n>>m;
- for(int i=1;i<=n;i++){
- scanf("%d %d",&s[i],&v[i]);
- }
- ll mid,l=0,r=2e9;
- while(l<=r){
- mid=(l+r)>>1;
- if(check(mid)) r=mid-1;
- else l=mid+1;
- }
- if(check(l))cout<<l;//对二分查找失败的情况进行特判
- else cout<<-1;
- }

题目:公园
今天是六一节,小度去公园玩,公园一共 N 个景点,正巧看到朋友圈度度熊也在这个公园玩,于是他们约定好一块去景点 N。 小度当前所在景点编号为 T,从一个景点到附近的景点需要消耗的体力是 TE,而度度熊所在景点编号为 F ,移动消耗为 FE。 好朋友在一块,赶路都会开心很多,所以如果小度和度度熊一块移动(即在相同位置向相同方向移动),每一步他俩的总消耗将会减少 S。
求他俩到景点 N 时,所需要的总消耗最少是多少?

输入:
4 4 3 1 2 8 8 1 4 2 3 3 4 4 7 2 5 5 6 6 8 7 8
输出:
22
思路:
其实注意到两个人的消耗是固定的,既然不知道在哪相遇,不妨把每个点都做中间相遇点试试,(你看看,出题人就是想让你暴力的)。
我们先对3个点找各自到其他点的最短距离,假如a点是相遇点,那么三个点(小度,小熊,终点)到此点a的最短距离×各自三个消耗(消耗怎么算?就看走了多长就行,因为每短的消耗是一样的),这样的话,一种答案就出来了,然后找出最优答案即可。
其实,从这道题,你发现了什么?是不是找3个点的最近距离问题!
- #include <bits/stdc++.h> //公园:共n个景点,两个人都要到n景点,两人移动一个景点就各消耗e1,e2,一起走消耗减少e3。求最少消耗?到不了输出-1
- using namespace std; //暴力枚举
- typedef pair<int,int> pa;
- const int N=40005;
- int dis[3][N],head[N];
- int s1,s2,n,m;
- long long ans=1e17;
- priority_queue<pa,vector<pa>,greater<pa>> Q;
- struct node{int to;int next;}e[N*2];
- void add(int u,int v){
- static int i=0;i++;
- e[i].to=v;
- e[i].next=head[u];head[u]=i;
- }
- void dijkstra(int s,int dis[]){
- for(int i=0;i<=n;i++)dis[i]=40000;
- dis[s]=0;
- Q.push(make_pair(0,s));
- while(!Q.empty()){
- int u=Q.top().second;int dis_=Q.top().first;Q.pop();
- if(dis_!=dis[u]) continue;
- for(int i=head[u];i;i=e[i].next){
- int v=e[i].to;
- if(dis[v]>dis[u]+1)
- dis[v]=dis[u]+1,Q.push(make_pair(dis[v],v));
- }
- }
- }
- int main(){
- long long e1,e2,e3; //之所以ll型,是因为dis是int型,运算时方便给ll型ans赋值(类型隐式转换)
- cin>>e1>>e2>>e3; //e1,e2是两人的消耗,e3是减少的消耗:
- cin>>s1>>s2>>n>>m;//s1,s2是两个人的起点,n,m是景点数和边数
- int u,v;
- while(m--){
- scanf("%d %d",&u,&v);
- add(u,v);add(v,u); //建边
- }
- dijkstra(s1,dis[0]); //寻找3个点到其余点的最短距离
- dijkstra(s2,dis[1]);
- dijkstra(n,dis[2]);
- for(int i=1;i<=n;i++){ //如果dis没有变说明这个点到不了,标记一下
- if(dis[0][i]==40000)dis[0][i]=-1;
- if(dis[1][i]==40000)dis[1][i]=-1;
- if(dis[2][i]==40000)dis[2][i]=-1;
- }
- for(int i=1;i<=n;i++){
- if(dis[0][i]!=-1&&dis[1][i]!=-1&&dis[2][i]!=-1) //3个点都要能到才算有效(能连起来)
- ans=min(ans,dis[0][i]*e1+dis[1][i]*e2+dis[2][i]*(e1+e2-e3)); //(ll*int)->ll类型
- }
- if(ans==1e17){cout<<-1;return 0;}//3个点没有一个公共交点,即3个点连不起来
- cout<<ans;
- return 0;
- }

新材料
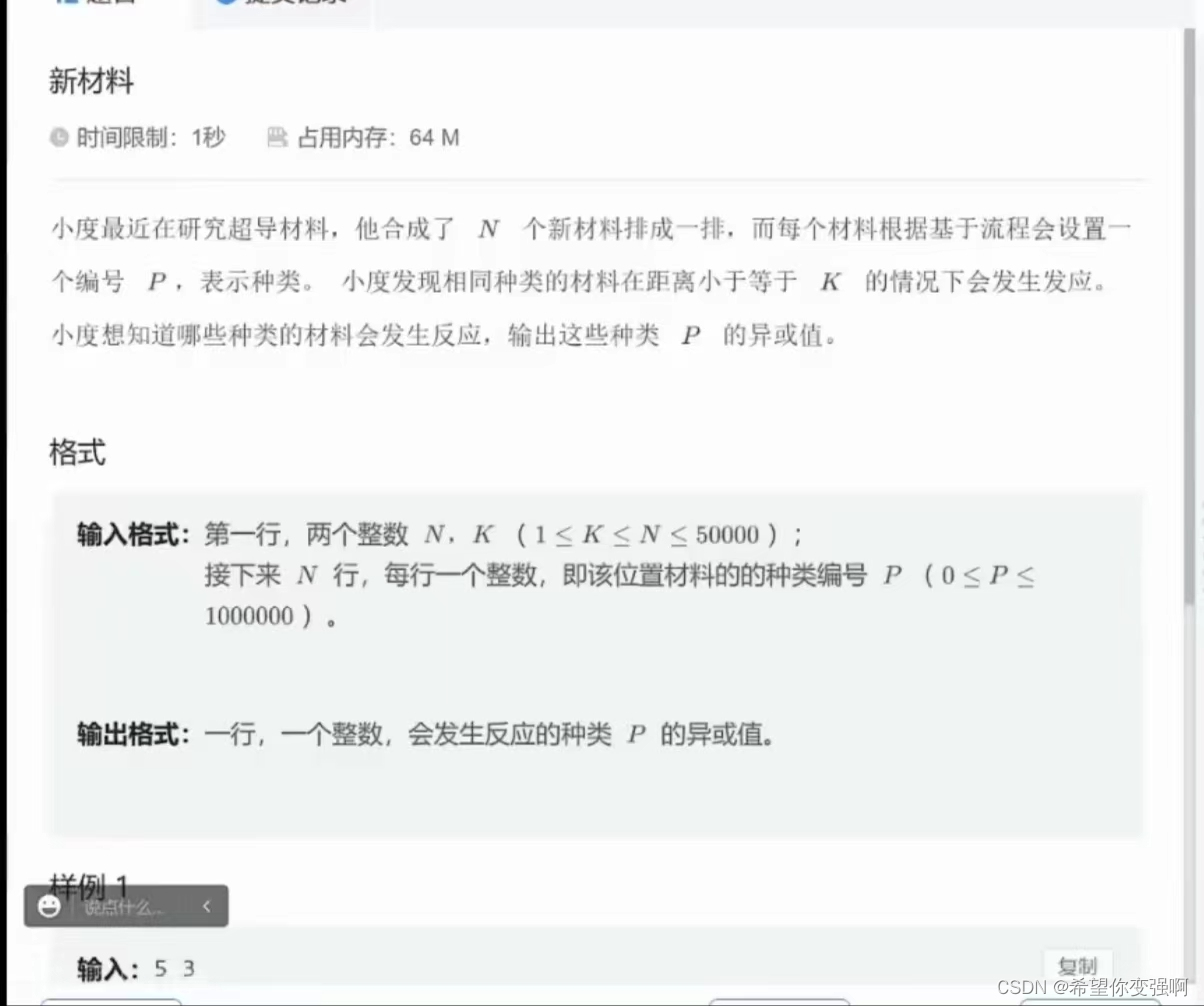
思路:
直接模拟:因为要考虑上次出现的位置,所以使用map映射最好,如果没有出现过就建立新映射,如果出现过但是已经反应过就跳过,如果出现过但是不足以反应,就建立新映射,如果能反应就反应,并标记。
- #include <bits/stdc++.h>
- using namespace std;
- map<int,int>mp;
- int n,k;
- int main(){
- scanf("%d%d",&n,&k);
- int ans=0;
- for(int i=1;i<=n;i++){
- int cur;scanf("%d",&cur);
- if(!mp.count(cur))mp[cur]=i;//有返回1无返回0,返回-1表示已经反应过了
- else if(mp[cur]==-1)continue;
- else if(i-mp[cur]>k)mp[cur]=i;
- else ans^=cur,mp[cur]=-1;
- }
- cout<<ans<<'\n';
- }

星际航行


思路:
我们的任务是把三维的一群点,变成任意两维都相同,另一维是个差为1的等差数列,然后求最小代价。其实我们可以枚举下哪两维相同,然后计算代价,再计算剩下的一维变成等差数列的代价。
任务1:把一个维度上的所有点变到同一个位置的最小代价就是把所有点都挪到中间点上,你可以画图证明:每两个点之间挪动的代价恰好都是两点之间的线段距离的情况下,总代价最小。
如图:我们只要保证更多的点分布在中间点的两边,且两边的点都恰好连成线段时候代价是最小的(这个偶数的点的情况,奇数的点的情况会更加明显)
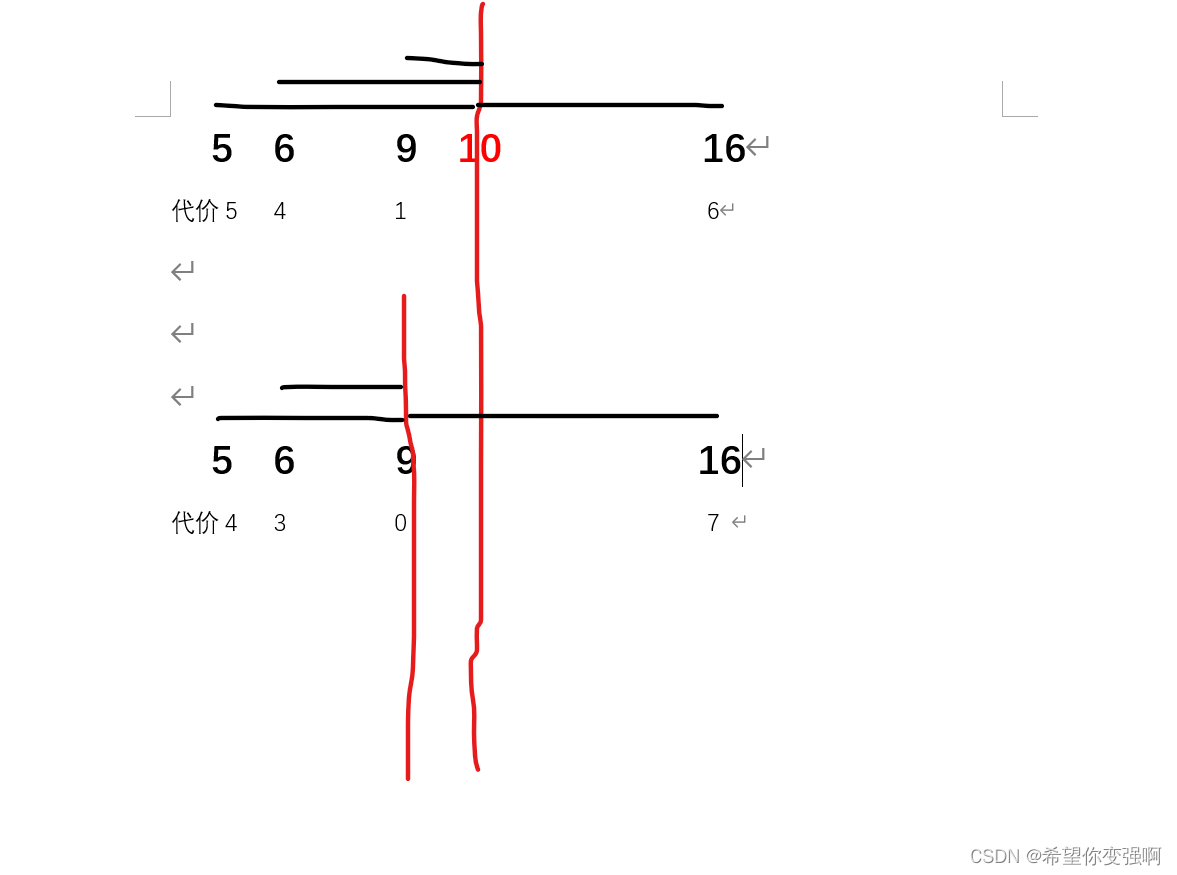
(上面的的是选10为中间点,下面的是选9为中间点)
任务2:要把一个维度上所有点变成一个等差数列且代价最小,就必须不能改变它们之间原来的顺序。如图:(我们假设最终的点的起点是t,那么所有点最终坐标是t+i)

那么最终的代价是sum|xi-(t+i)|最小,然后我们再变形一下:sum|(xi-i)-t|,诶,这不就是所有点xi-i到t的代价最小吗,我们只需要在重复一下上面任务1的做法就行了。
那么最终做法就是:先把数组排序,然后找到求每个点到中间的点的距离和,最终求出两个度的代价,然后在求ai=ai-i,再做一遍,这样就枚举出了一种情况了,然后把所有情况都枚举一下就行了。
题目:蛋糕划分
小度准备切一个蛋糕。这个蛋糕的大小为 N∗N,蛋糕每个部分的重量并不均匀。
小度一共可以切 K刀,每一刀都是垂直或者水平的,现在小度想知道在切了 K刀之后,最重的一块蛋糕最轻的重量是多少。

思路:
首先这个暴力dfs不行,横刀14下,竖刀14下,共2^28*14^2会超时的
其实对最大质量的蛋糕块二分答案即可,难在对答案判断:
首先我们对所有的横刀状态模拟,用一个数的(n-1)位的表示所有状态即可,然后根据此时横刀状态对竖刀进行决策,方法是:
从第一列开始,计算每列区间和,若此时横刀区间和加上新的一列区间后值大于答案了,那就要在此列左边切竖刀,然后在此竖刀右面重新计算新一列区间,
不断重复。其实就是每个横刀区间加上新一列区间后都不要大于答案,如果大于我们就要这里要切竖刀了。最后统计竖刀和横刀数,返回结果即可
(另外,为了加速处理,还要用上二维前缀和)
- #include <bits/stdc++.h> //蛋糕划分:蛋糕大小N*N,每个部分质量不均,共切k刀(横竖均可),使最重的一块蛋糕的质量最轻是多少。
- using namespace std; //2≤N≤15,1≤K≤2N−2 ,每个位置质量W小于1000 和洛谷P1182 数列分段一样思路
- int n,k,fal,max_;//fal是答案出错标记,方便快速结束循环
- int a[20][20],sum[20][20],col[20],cnt[20],temp[20];;//col存放竖刀的位置,cnt是横切后每个区间和,temp是新一列区间和
- int get_sum(int x1,int y1,int x2,int y2){//求上下左右区间和
- return sum[x2][y2]-sum[x2][y1-1]-sum[x1-1][y2]+sum[x1-1][y1-1];
- }
- bool check(int m){
- if(m<max_)return false;//特判
- //第一个循环是对每种横刀状态进行遍历(每一个i都代表一种横刀状态)
- for(int i=0;i<(1<<(n-1));i++){
- fal=0;//更新此种横刀状态为正确,内部循环发现是因横刀出错时就一头冲出来
- memset(col,0,sizeof(col));
- memset(cnt,0,sizeof(cnt));
- memset(temp,0,sizeof(temp));
- vector<int> v;
- int count=0,ans=0, tmp=i;
- while(tmp){
- count++;
- if(tmp&1){//获取i中1的位置,存入这种状态下的每个横刀位置
- v.push_back(count);//v用来存横刀位置,若v里面为1,3,4,加入n后,表示横刀区间1-1,2-3,4-4,5-n
- ans++;
- }
- tmp/=2;
- }
- if(ans>k)continue;//特判
- v.push_back(n);
- int p=0,top=1,down;//top是该区间最上面元素位置,down是此横刀位置,p为当前的第几个横刀区间(
- //第二个循环是切竖刀的,在每个竖位置遍历列区间,一旦某个横刀区间加上这个列超过答案就说明可以切竖刀了
- for(int j=1;j<=n;j++){
- p=0,top=1;//每切一次竖刀就重置一次
- //第三个循环是遍历横刀区间的(我们要自上而下遍历每个区间)
- for(int x:v){//用x来访问v中的所有元素,取出每个横刀位置
- down=x;
- int now=get_sum(top,j,down,j);//求列区间和(列宽为1)
- if(now>m){//如果仅列区间已经大于答案就说明是横刀状态失误了,fal标记一下,直接冲到最外面
- fal=1; break;
- }
- //求新的横刀区间(原横刀区间加列区间)
- cnt[++p]+=now;//将上个区间加上这个区间
- if(col[j-1]){
- cnt[p]=now;//上个位置被切过了,就说明我们不应该加的
- }
- temp[p]=now;//temp存每个列区间和
- //判断该横刀区间,决策是否切竖刀
- if(cnt[p]>m){//该区间和大于答案,说明要切竖着在j-1的位置一刀,cnt再从第j列开始计算和(你只有犯错的时候才知道自己犯错了)
- col[j-1]=1;//更新竖切的位置和区间和
- cnt[p]=now;
- for(int ii=1;ii<p;ii++)cnt[ii]=temp[ii];//之前的区间也要因此而更新了,用上temp了
- }
- top=down+1;//top是下个区间最上面位置
- }
- if(fal)break;
- }
- if(fal)continue;
- for(int j=1;j<=n-1;j++)
- if(col[j])ans++;//col存放的竖切刀
- if(ans<=k)return true;
- }
- return false;
- }
- int main(){
- cin>>n>>k;
- for(int i=1;i<=n;i++)//数据从1,1开始存,后面注意这点
- for(int j=1;j<=n;j++){
- cin>>a[i][j];
- max_=max(max_,a[i][j]);
- sum[i][j]=a[i][j]+sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
- }
- int l=0,r=2000*15*15;
- while(l<=r){
- int m=(l+r)>>1;
- if(check(m)) r=m-1;//刀数太少,说明应该再切小一点
- else l=m+1;
- }
- cout<<l<<'\n';
- return 0;
- }

今天的确实有点难,嗯



