编译原理期末测试题总结_有限自动机的化简的题目

编译原理期末测试题总结

小结: 正规式和正规集

保留字，标识符，整常数等合法的单词符号构成正规集，每个正规集抽象成一个正规表达式。

上面集合也可以用正规表达式表达出来:
先把每一类单词表示成正规式
DIM正规式→{DIM}正规集
IF正规式→{IF}正规集
letter(letter|digit)*
digit(digit)*

状态转换图

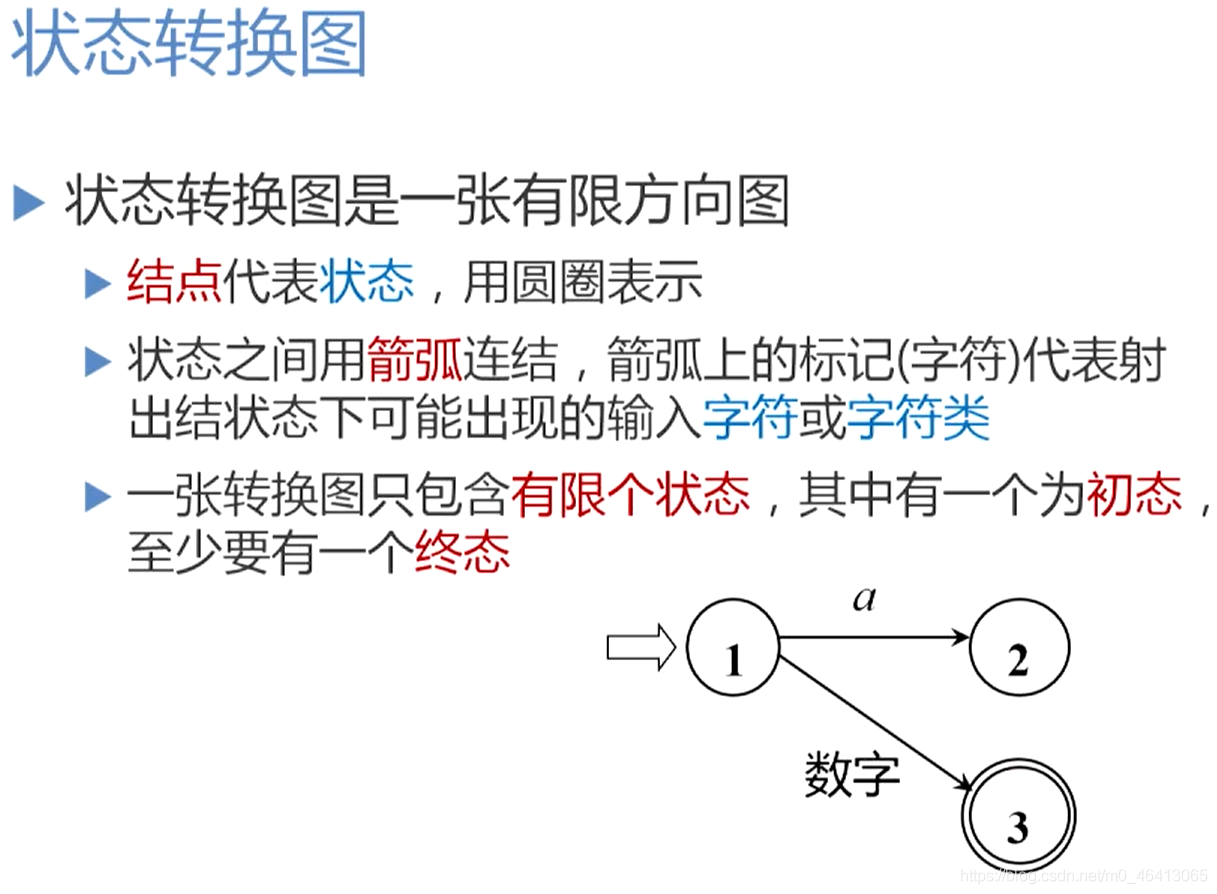
初态：有一个
终态：至少有一个

3.3.2 确定有限自动机(DFA)

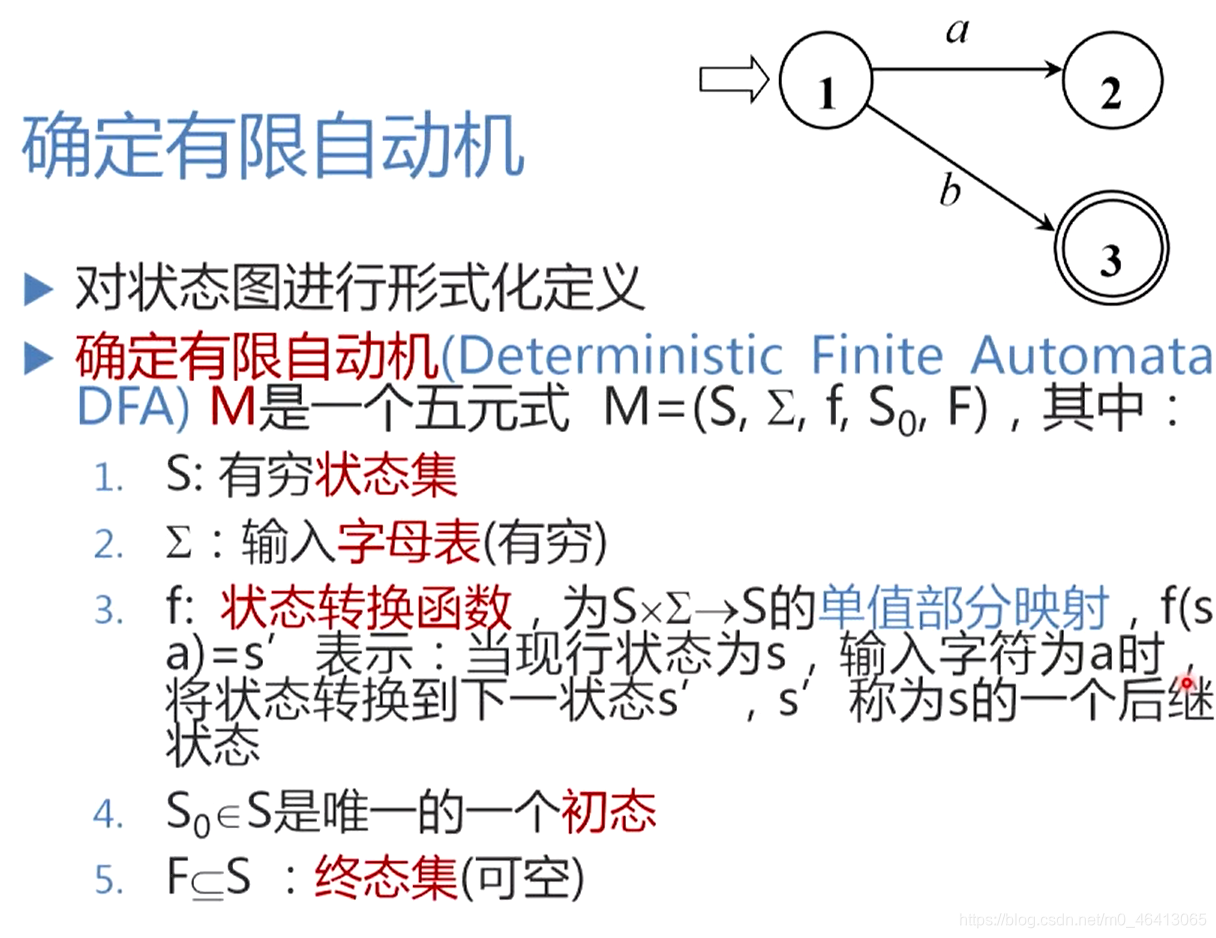
DFA允许没有终止状态

DFA可以表示为状态转换图。

• 假定DFA M含有m个状态和n个输入字符

• 这个图含有m个状态结点，每个结点顶多含有n条箭弧射出，且每条箭弧用Σ上的不同的输入字符来作标记

• 对于Σ^*中的任何字α，若存在一条从初态到某一终态的道路，且这条路上所有弧上的标记符连接成的字等于α，则称α为DFA M所识别(接收)

• DFA M所识别的字的全体记为L(M)。
  

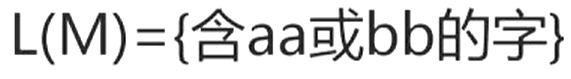
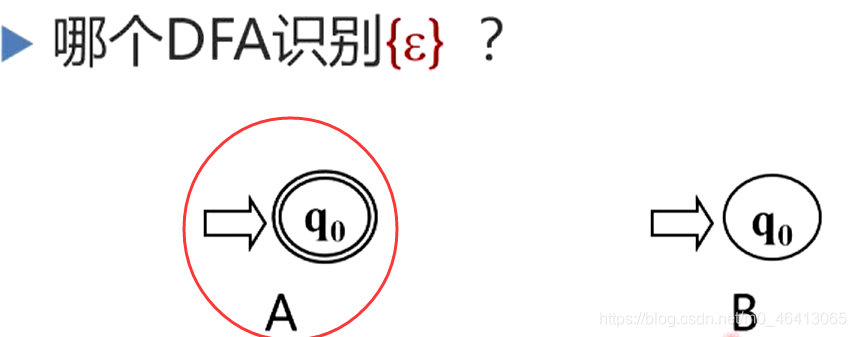
A:能识别空字$\epsilon$，系统初始就是q0状态，这个时候不读入任何字符，也是停留在q0状态，而q0又是终态。
或者说我从q0到q0是一条初态到终态的通路，这个通路上的边上的标记没有读入任何符号，所以没有转换关系，路径长度为0，字符串长度为0，但它又是从初态到终态的一条通路，这条通路上所标记的字符串就是空字$\epsilon$，所以说其能识别空字$\epsilon$。
即相当于从初态q0出发，读入了长度为0的字符串之后，继续停留在终止状态q0，也就是识别了空字$\epsilon$。

B:系统初始就是q0状态,又没有任何其他状态，也没有任何转换关系，因此，它永远找不到一条从初态出发到终态的道路，所以它不能完成任何字的识别，所以它识别的字的全体为空集$Ф$（区别于上述由空字$\epsilon$构成的集合）

3.3.3 非确定有限自动机(NFA)

• DFA初态唯一(确定性)
  NFA初态可以有多个，即其起始状态可以从不同的状态出发（非确定性）
• DFA状态函数为单值的部分映射，转换关系后继唯一。(确定性)
  NFA从一个状态识别一个字之后所到到达的后继状态可能是多个，不唯一。(非确定性)

从状态图中看NFA 和DFA的区别：

1. NFA可以有多个初态
2. 弧上的标记可以是Σ*中的一个字，而不一定是单个字符；
3. 同一个字可能出现在同状态射出的多条弧上。

DFA是NFA的特例

问题：是不是正规式的闭包必须用正规集来求？

b*c是一个正规式，对应了一个正规集{c,bc,bbc,…}这个转换关系说的是 从状态0出发，识别了这个正规式所对应的正规集当中的一个字之后就可以从0转到2，而1状态边上的标记可以理解为ab是一个字，表示从1出发识别ab这个字之后还是回到状态1。

甚至也可以把ab理解为一个正规式，这个正规式所对应的正规集里面只有一个字ab，也是识别了这个正规式中间所中的一个所对应的正规集当中的一个字之后从状态1转到状态1。

对状态2自圈弧上的标记是一个正规式a|b，这个正规式表示从状态2出发，识别了这个正规式所对应的正规集中间的一个字之后转到状态2，这个a|b的正规式所对应的正规集是{a,b}

DFA弧上的标记只能是字符
NFA弧上的标记可以是字符，可以是字，（可以是正规式,暂不考虑）。
p.s.字VS字符 字符组成字，字符一般指单个字符。

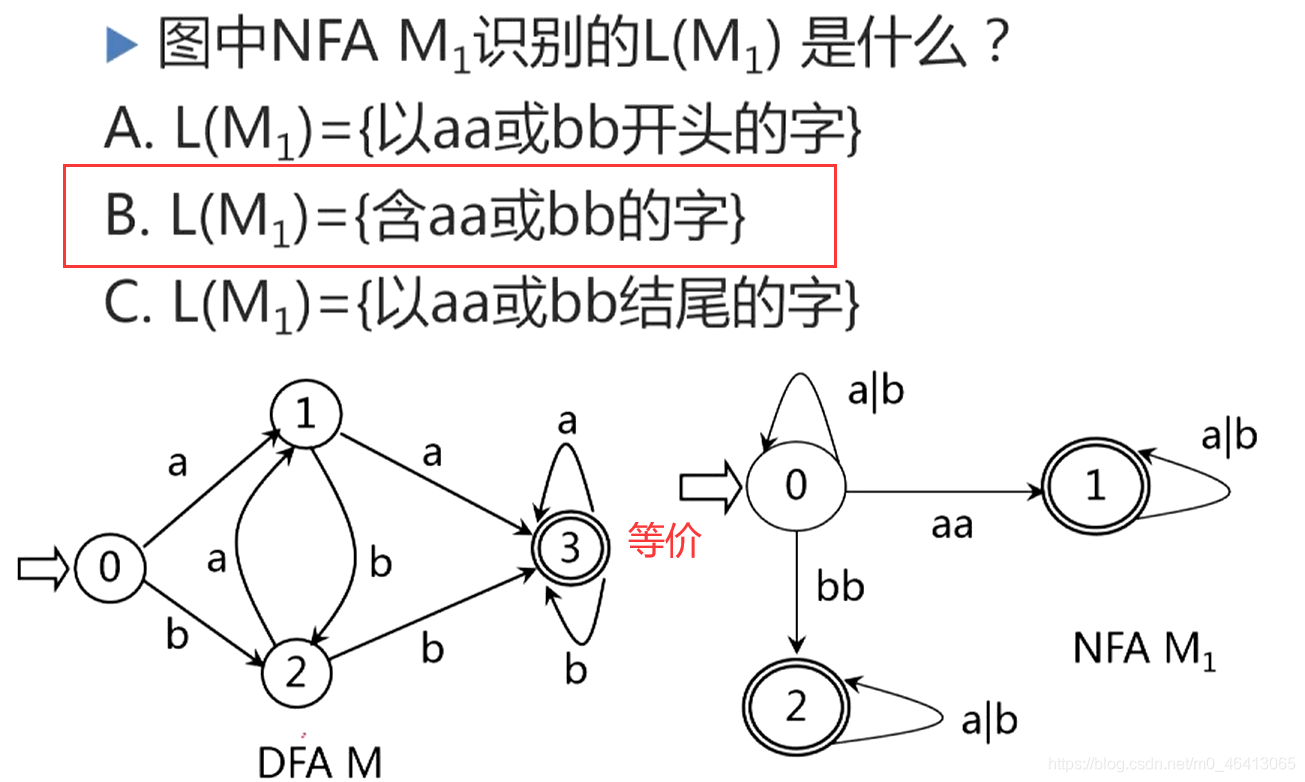
DFA与NFA区别：

1. DFA初态唯一(确定性)
   NFA初态可以有多个，即其起始状态可以从不同的状态出发（非确定性）

2. DFA弧上标记一定是单个字符
   NFA弧上的标记可以是Σ*中的一个字，而不一定是单个字符；

3. DFA状态函数为单值的部分映射，转换关系后继唯一。(确定性)
   NFA从一个状态识别一个字之后所到到达的后继状态可能是多个，不唯一。(非确定性)

DFA和NFA等价性

• 定义：对于任何两个有限自动机M和M’，如果L(M)=L(M’)，则称M与M’等价。
• 自动机理论中一个重要的结论：判定两个自动机等价性的算法是存在的。
• DFA与NFA描述能力相同。
  对于每个NFA M存在一个DFA M’，使得 L(M)=L(M’)。

DFA与NFA等价性证明

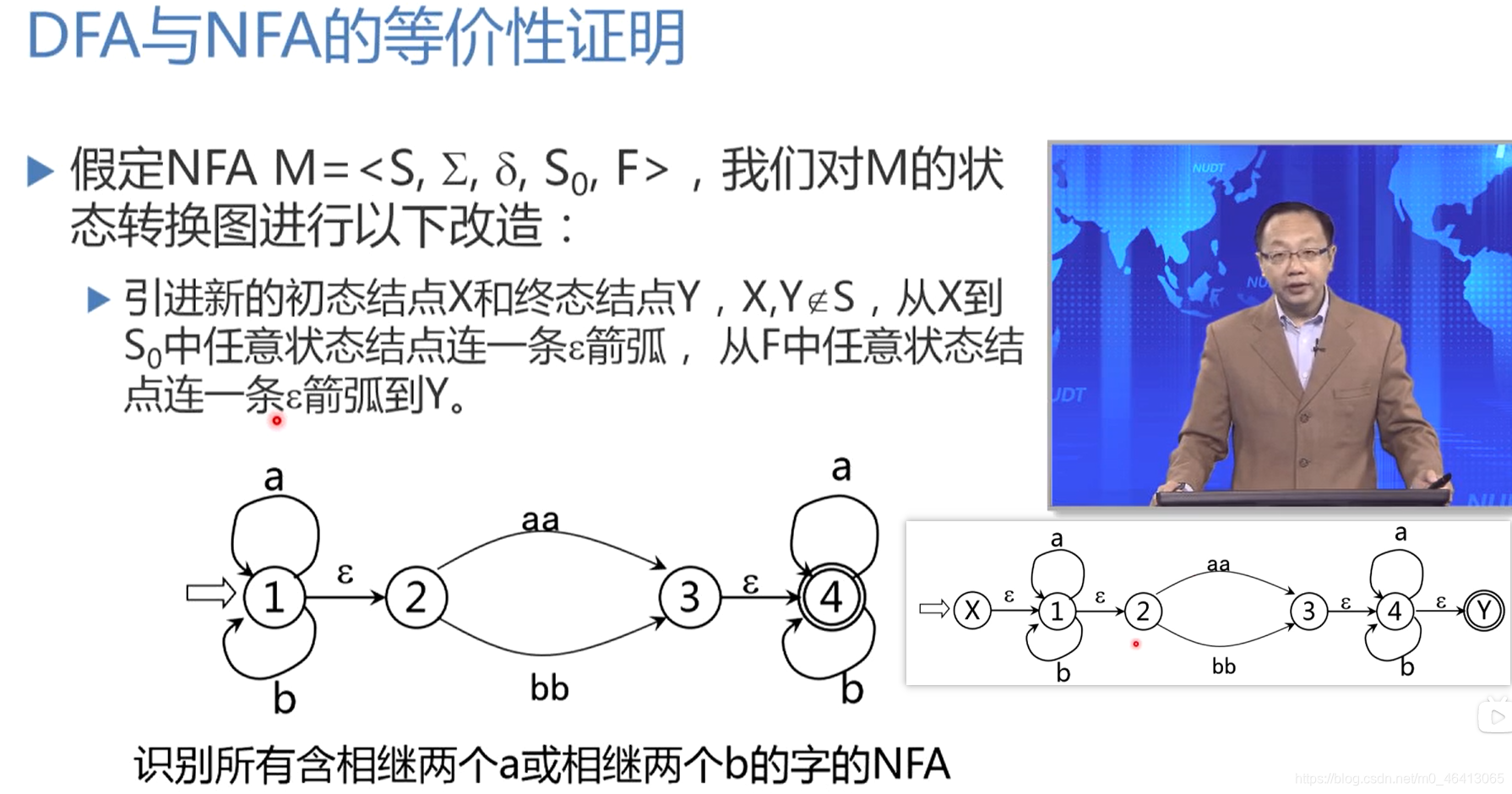
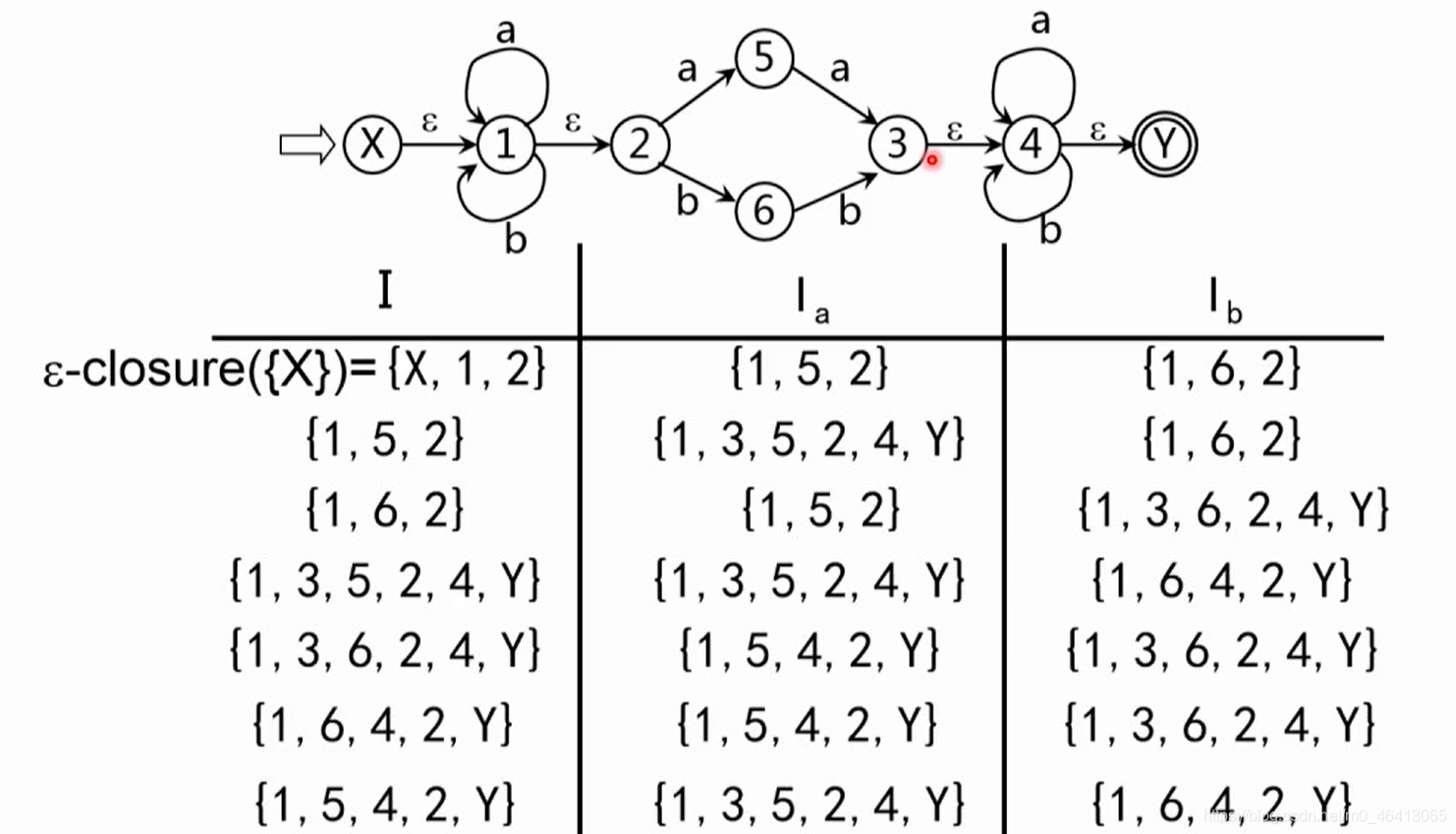
将XY分别作为唯一初态与终态，消除NFA和DFA在初始状态上的差异，解决了初始状态上唯一性问题。

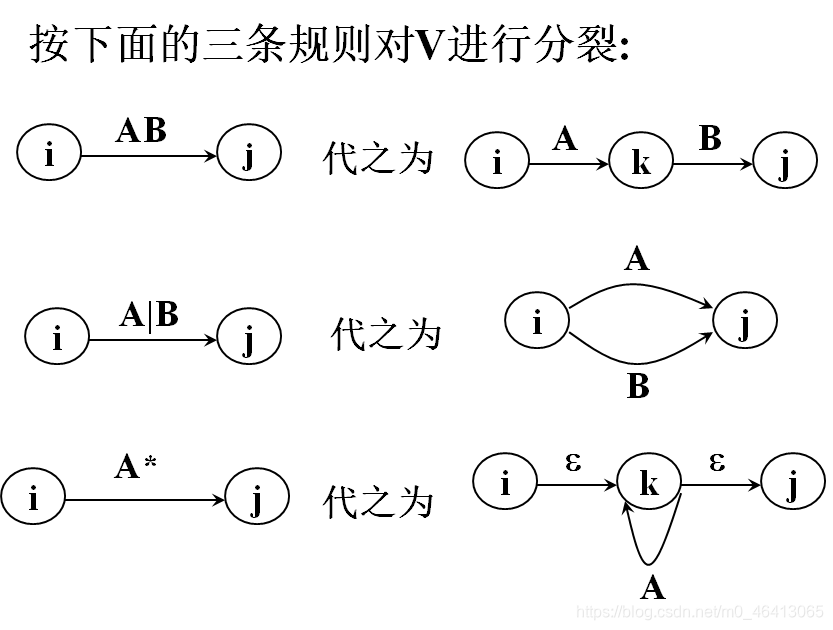
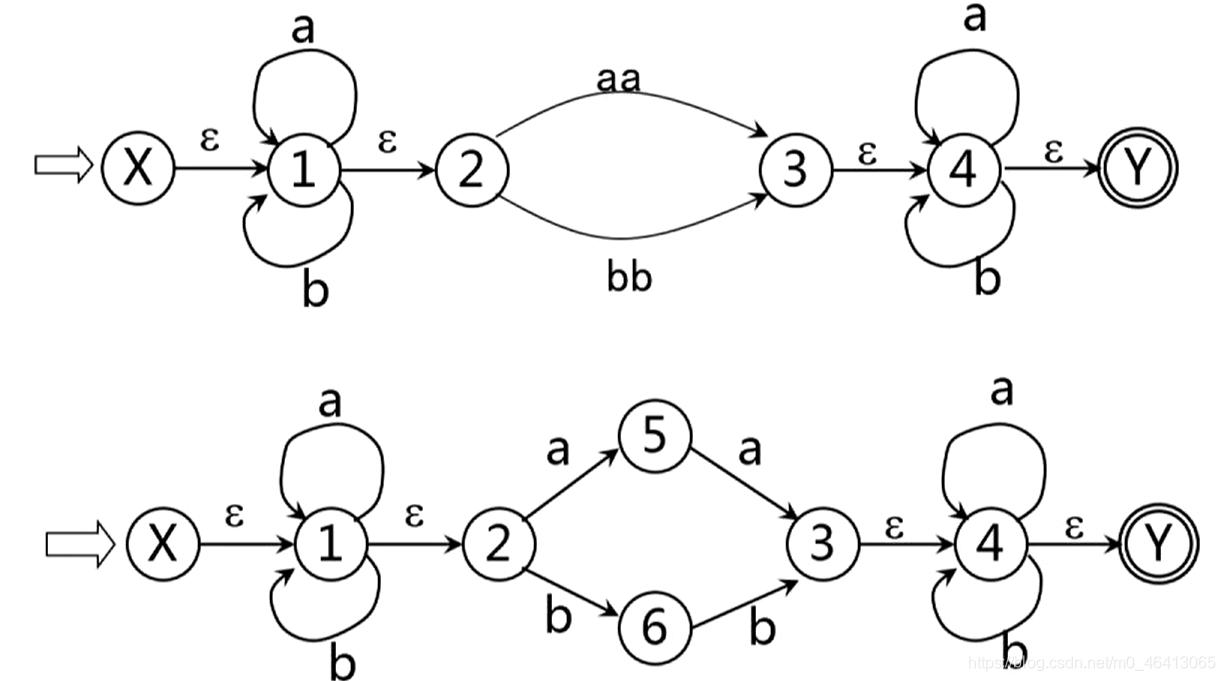
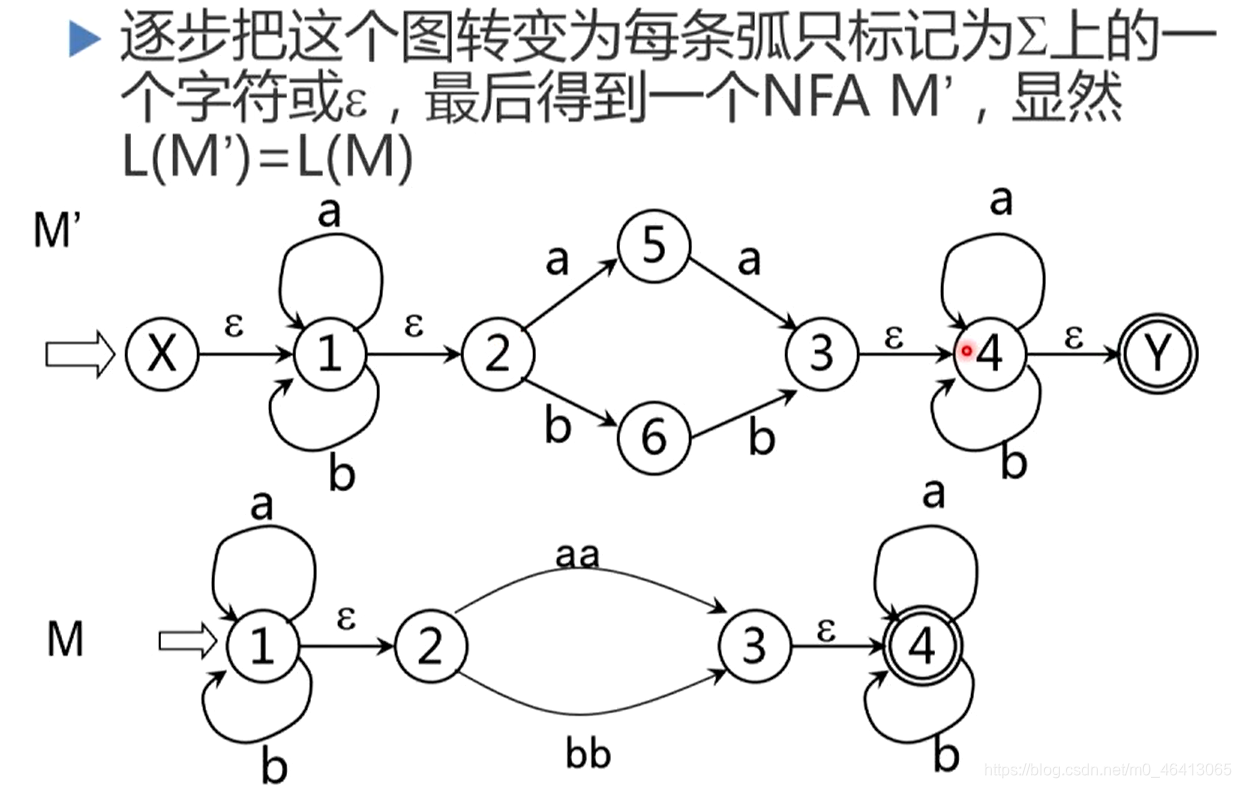
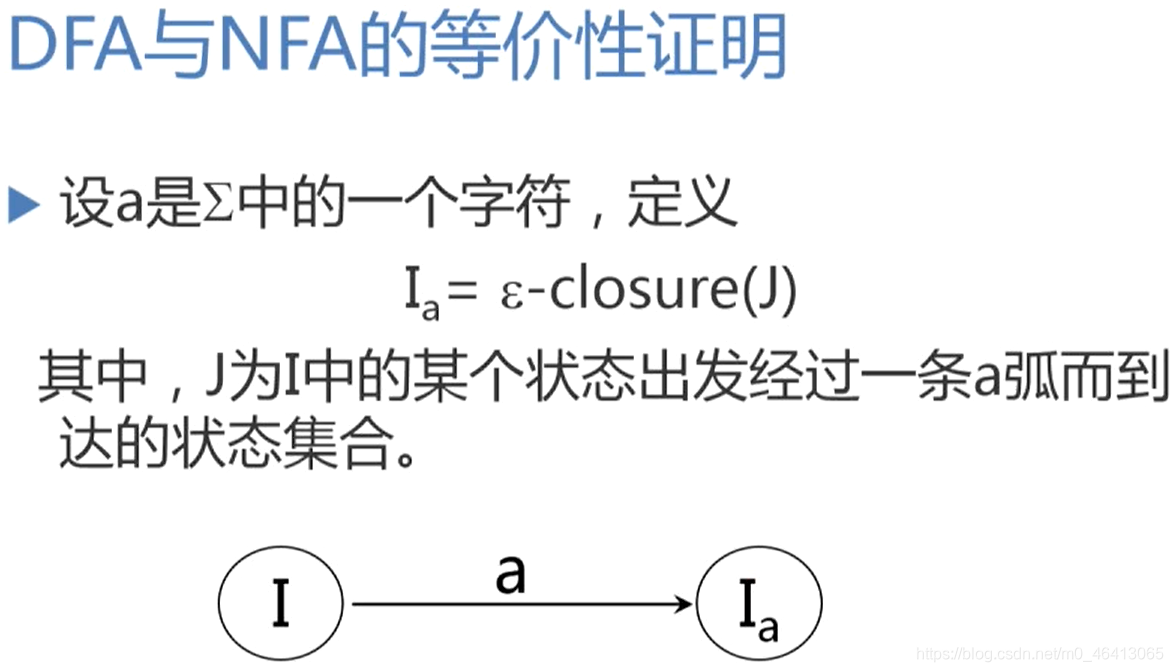
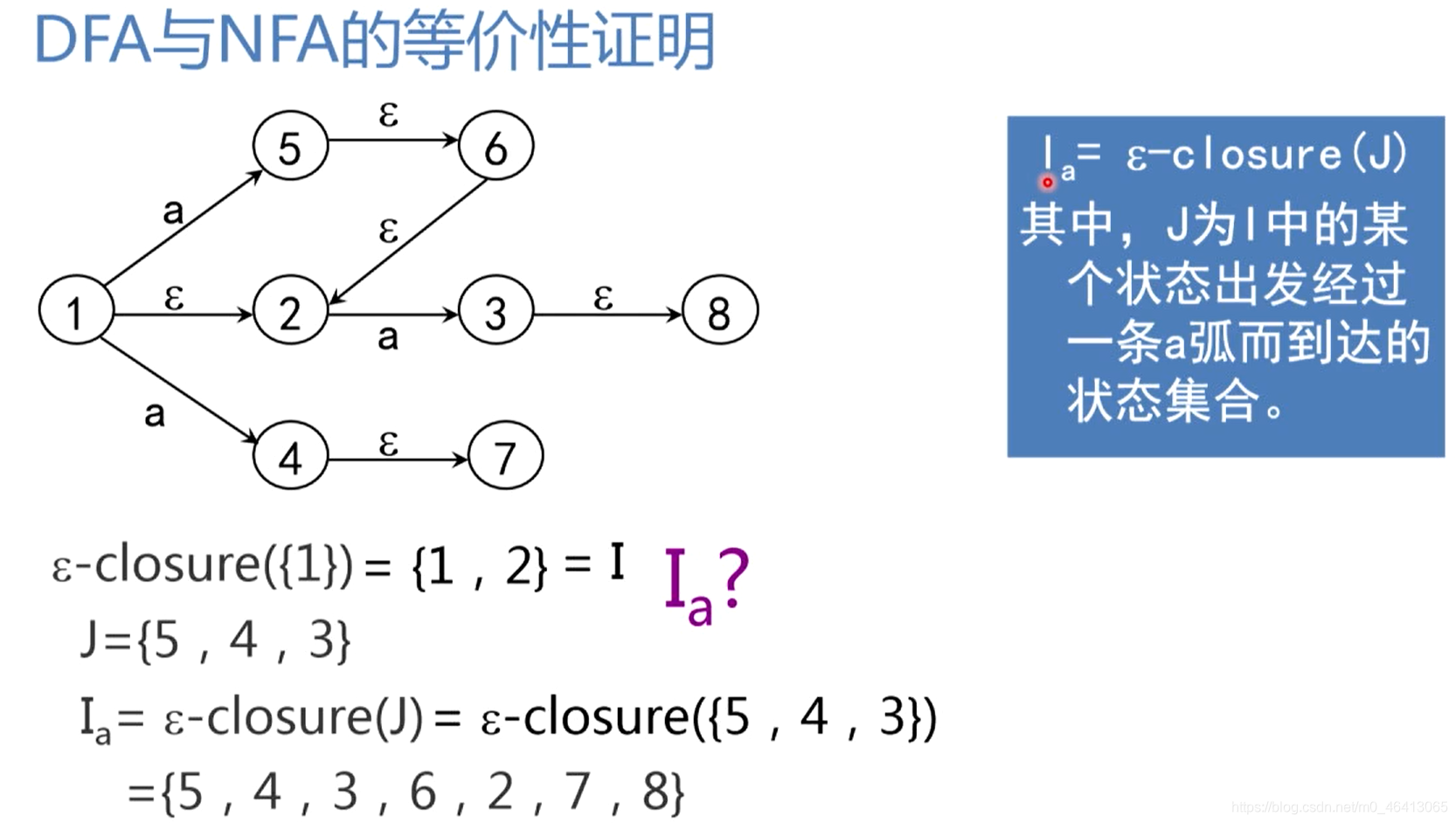
注意：如果算出来的Ia,Ib为空集$Ф$，空集$Ф$也要放在第一列中，虽然空集Ia,Ib也为$Ф$

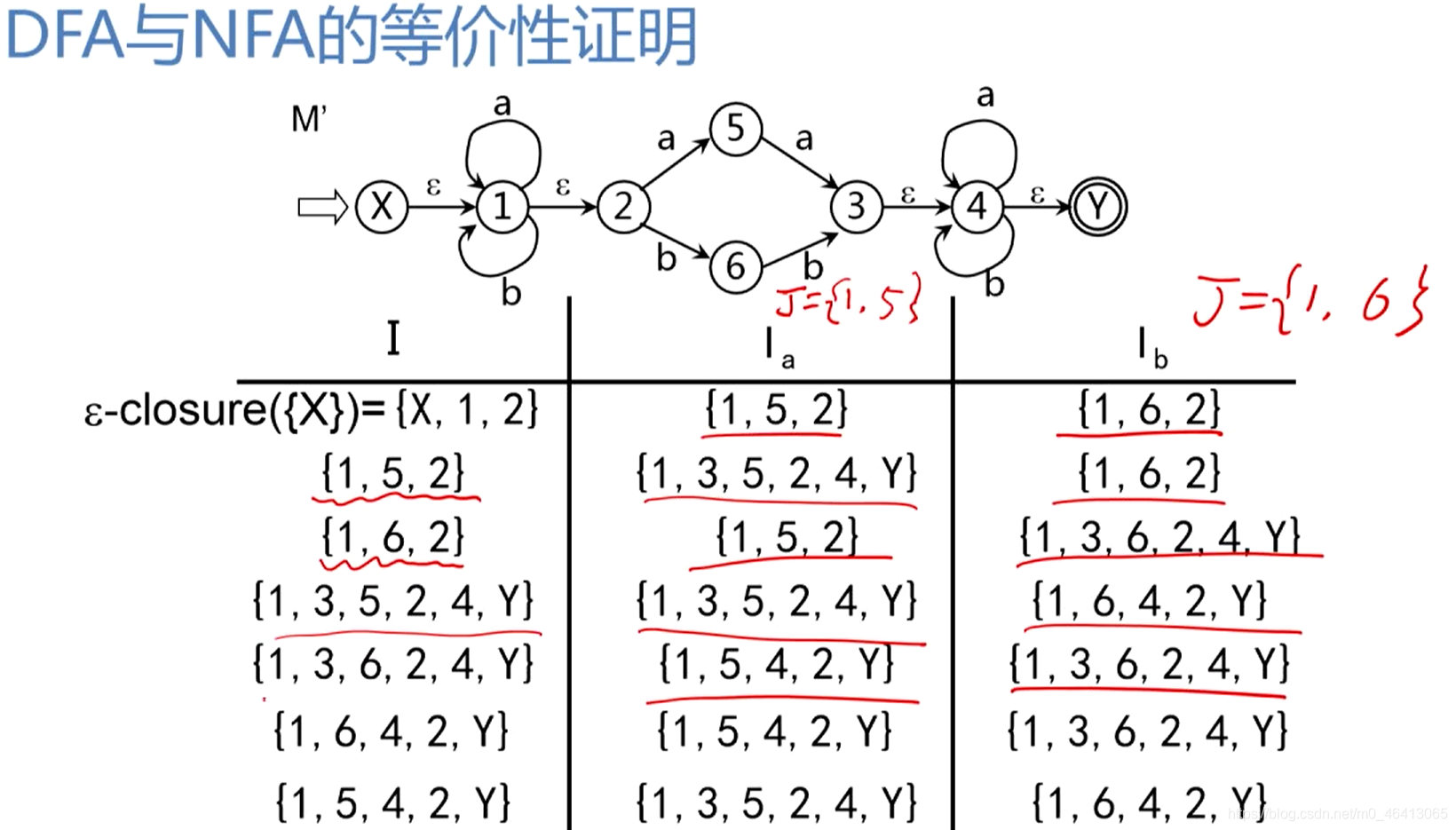
当所有第二列，第三列出现过的子集在第一列都已经计算过了，这个计算过程就可以停止。

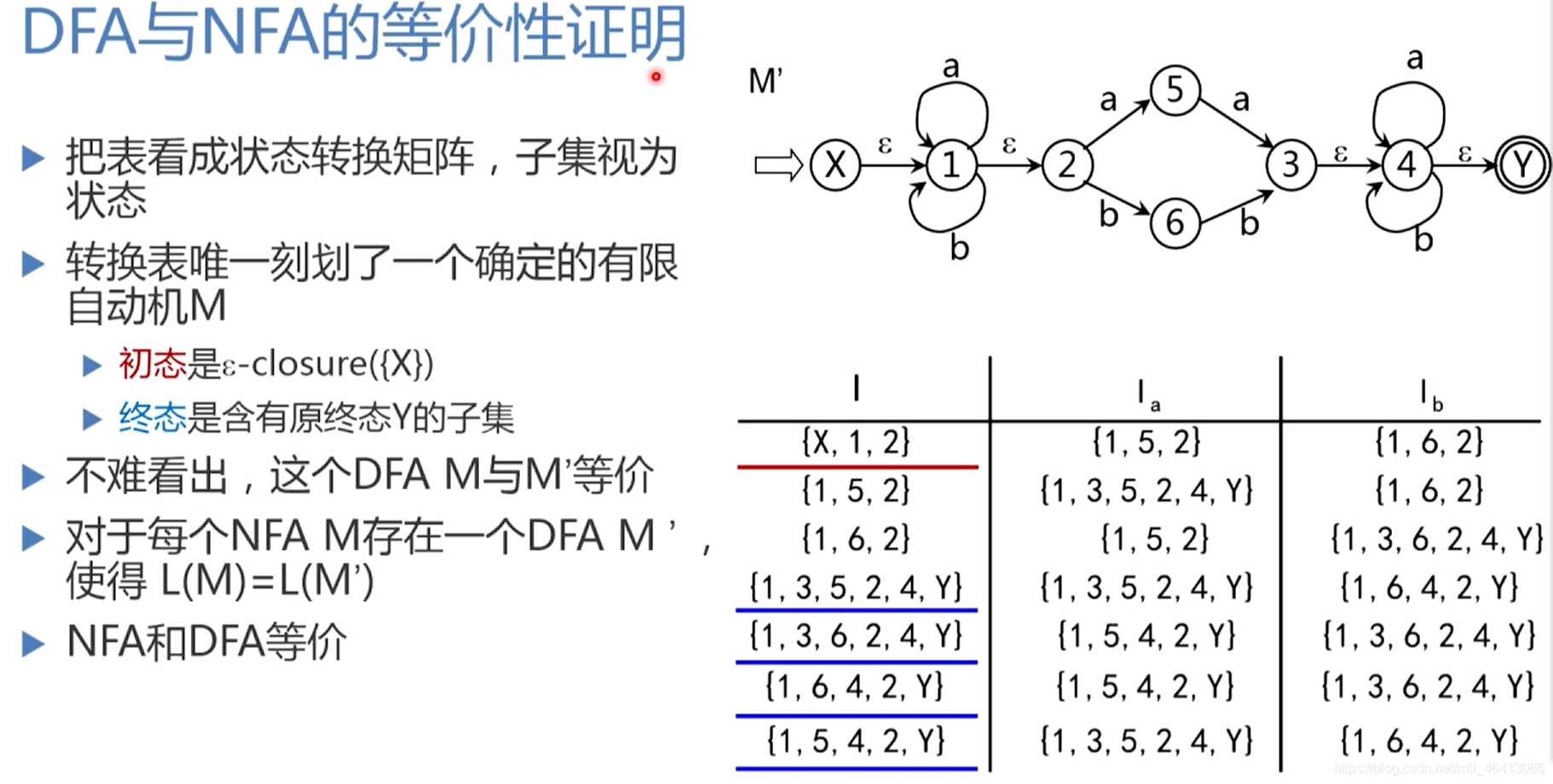
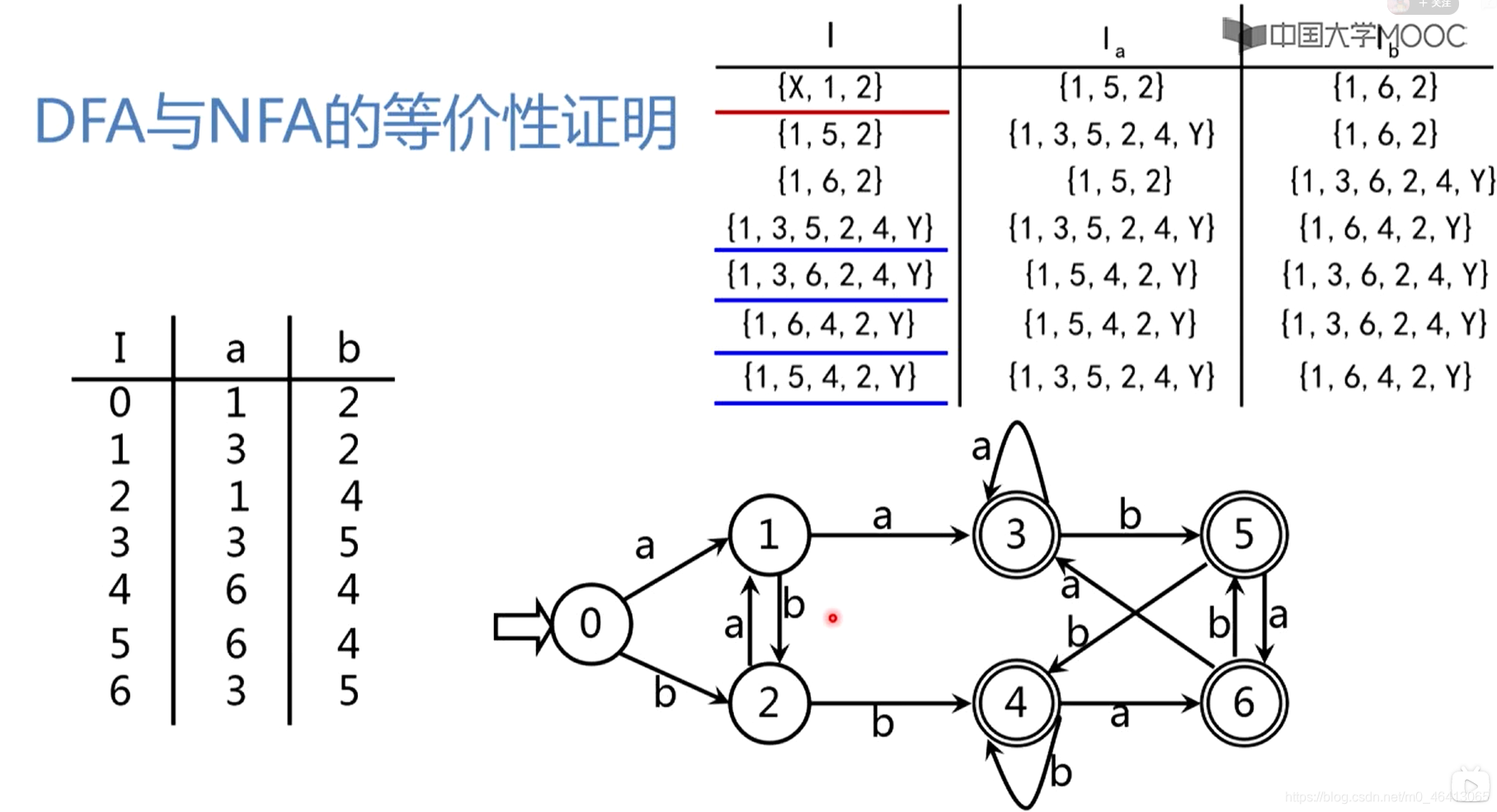
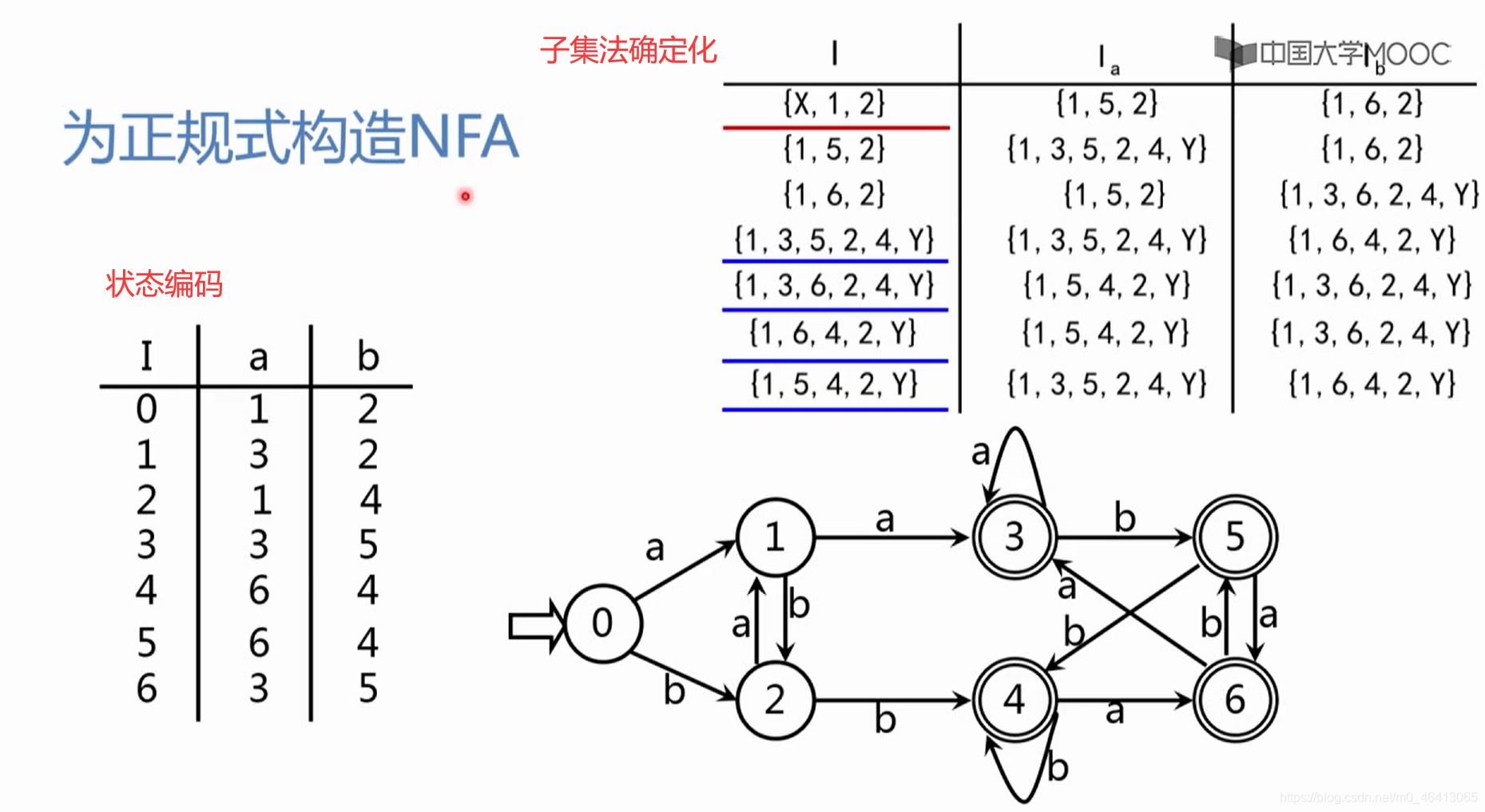
得到状态集之间的状态转换关系
给每个状态集进行编号，得到状态转换矩阵，再把它化成状态转换图

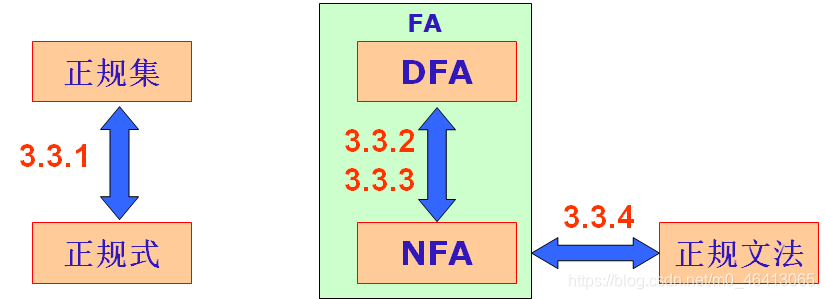
3.3.4 正规文法与有限自动机的等价性

定理：

1. 对每一个右线性正规文法G或左线性正规文法G，都存在一个有限自动机(FA) M，使得L(M)＝L(G)。
2. 对每一个FA M，都存在一个右线性正规文法GR和左线性正规文法GL，使得L(M)＝L(GR)＝L(GL)。

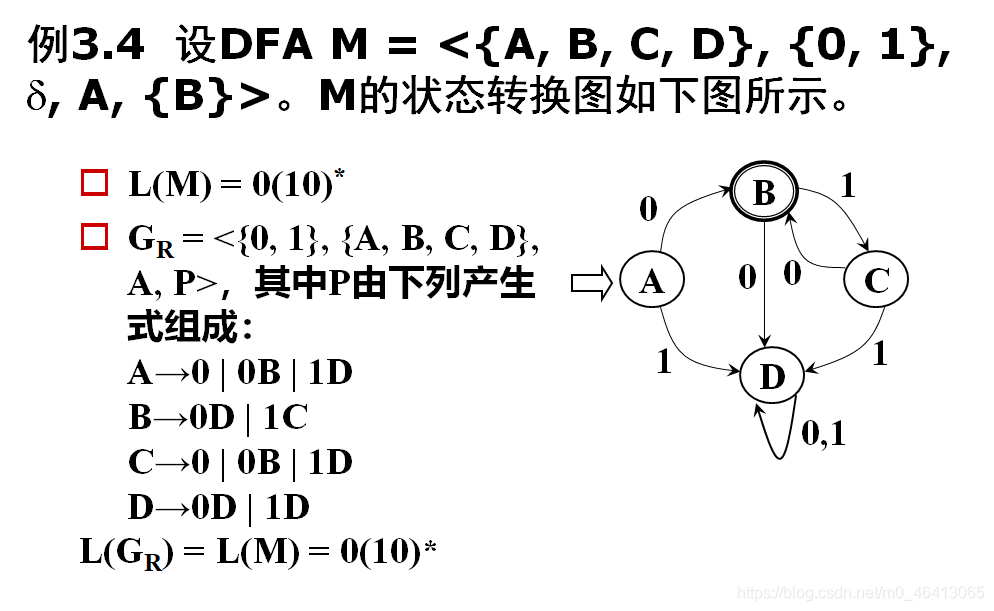
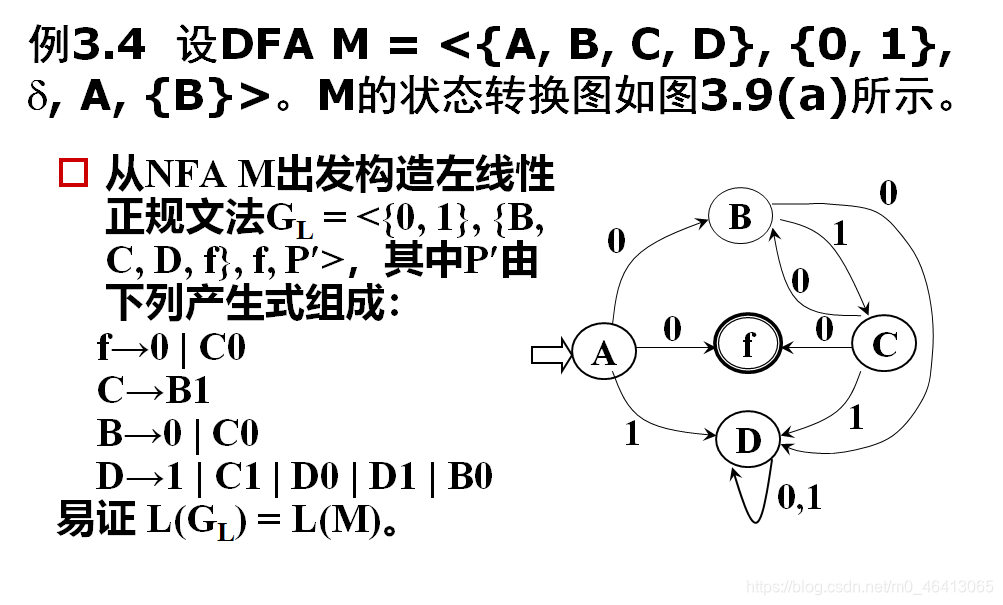
3.3.5 正规式与有限自动机的等价性

定理：

1. 对任何FA M，都存在一个正规式r，使得L( r )=L(M)。
2. 对任何正规式r，都存在一个FA M，使得L(M)=L( r )。

对转换图概念拓广，令每条弧可用一个正规式作标记。(对一类输入符号)

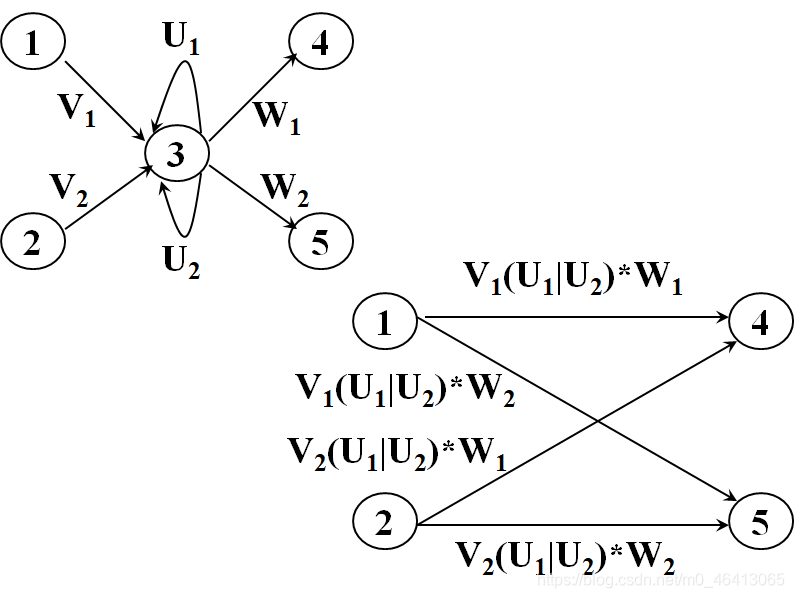
• 最后，X到Y的弧上标记的正规式即为所构造的正规式r
• 显然L( r )=L(M)=L(M’)
  
  
  
  
  
  
  
  
  
  
  
  

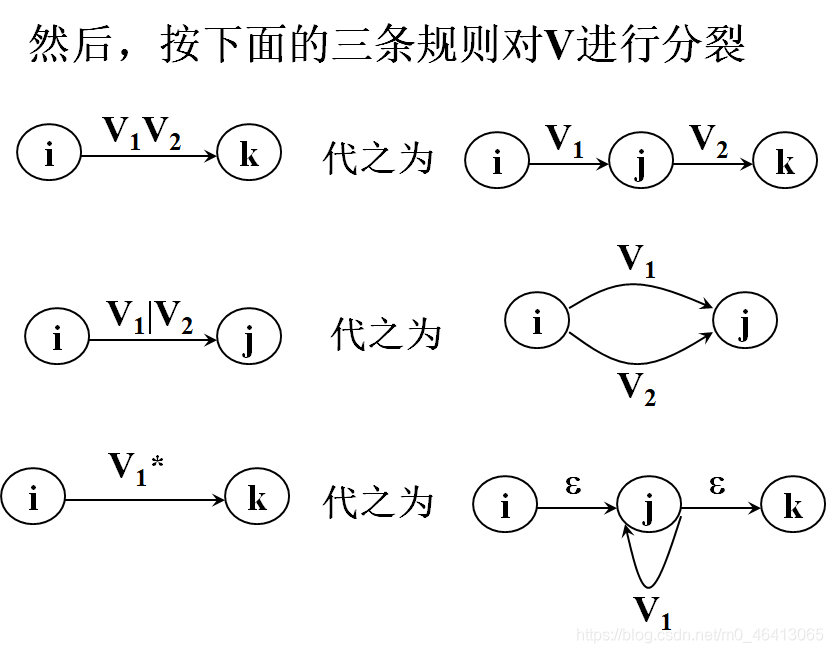
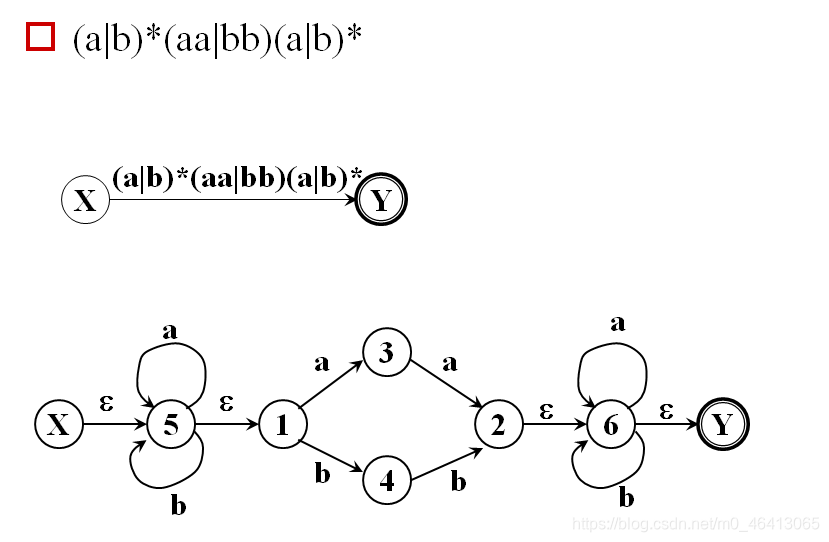
3.3.5’ 为NFA构造正规式

内容跟上面基本相同，细节可能略有不同，上面懂了这个可以跳过

然后，反复使用下面的三条规则，逐步消去结点，直到只剩下X和Y为止。

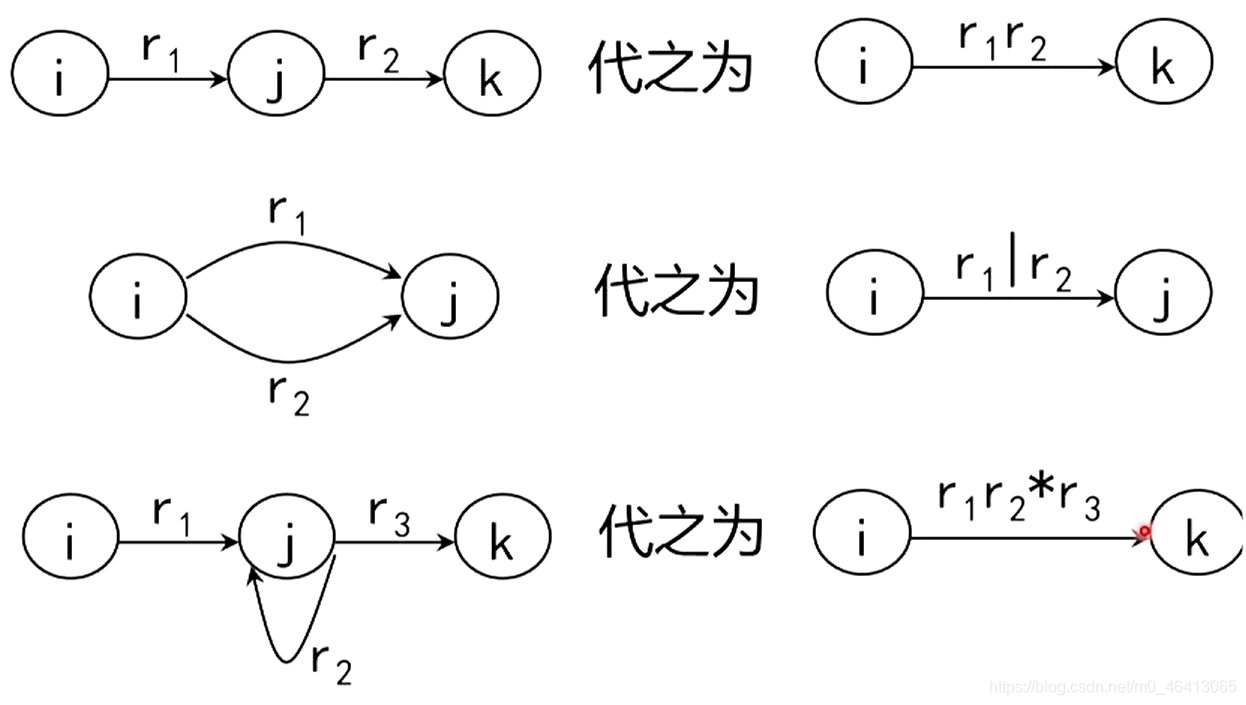
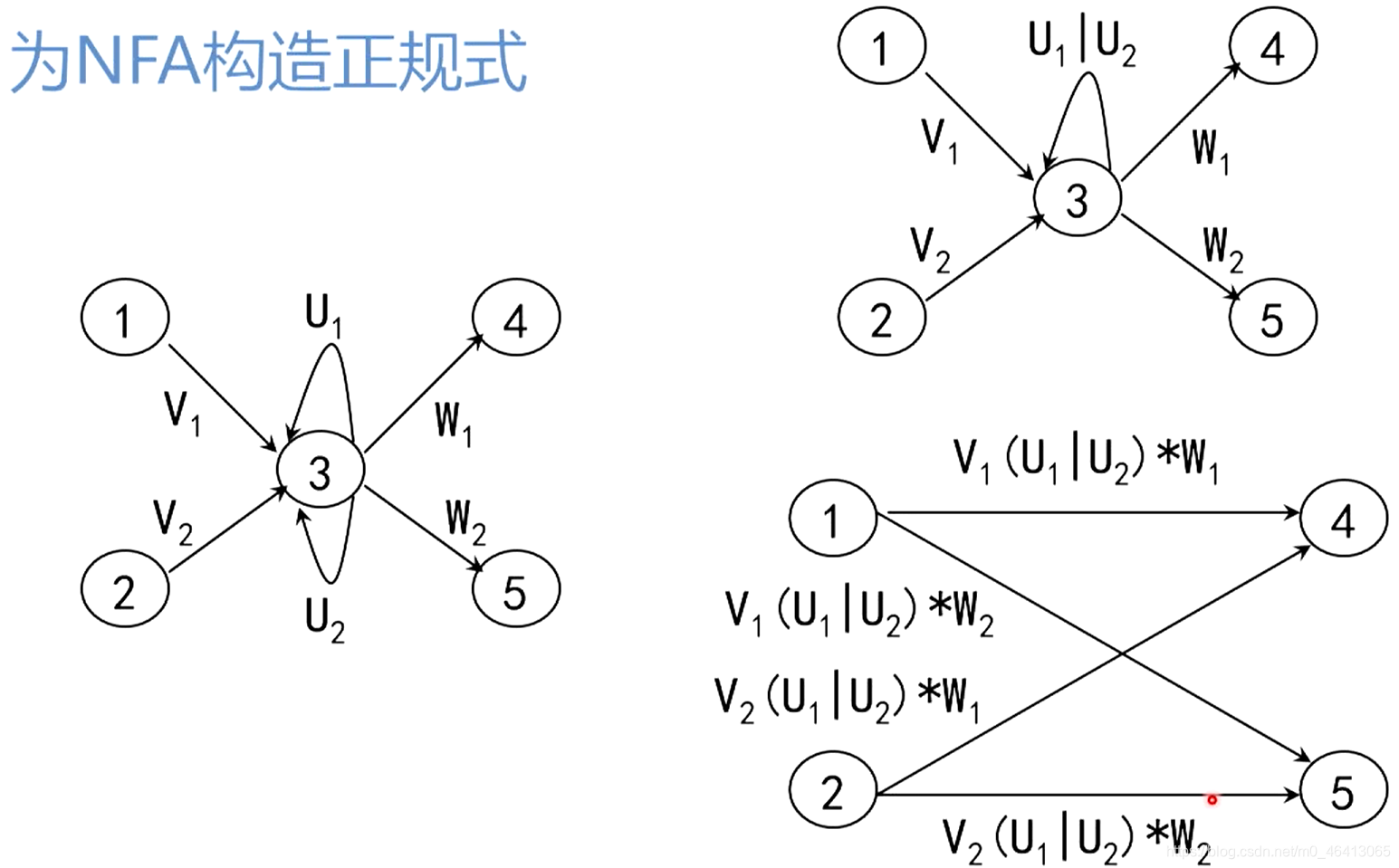
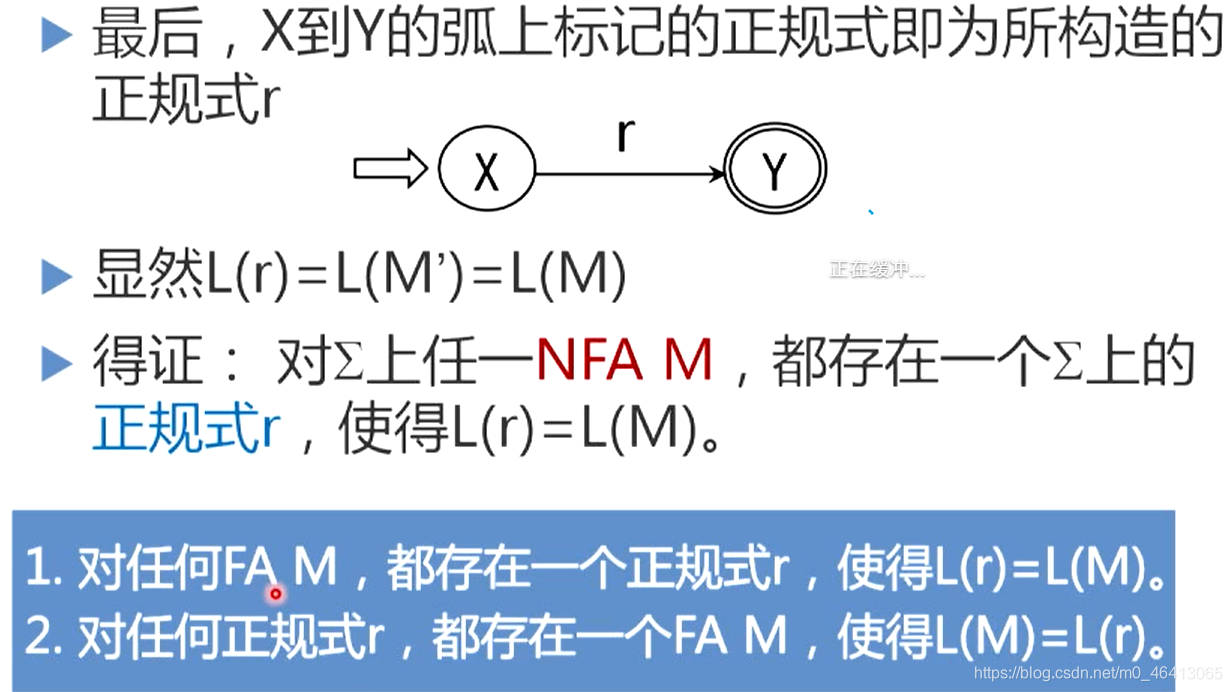
情形1 ： r=r1|r2

• 由归纳假设，存在L(M1)=L(r1)，L(M2)=L(r2)
• 引入两个新状态q0(唯一初态)和f0(唯一终态)
• 从q0分别射出两个ε弧到q1，q2
• M1,M2中的转换关系不变（保留M1,M2内部转换关系）
• 从f1，f2分别射出ε弧到f0
  
  

情形2 ： r=r1r2

• 由归纳假设，存在L(M1)=L(r1)，L(M2)=L(r2)
• 将M1唯一的初态q1作为最后构造出来的M的唯一的初态，将M2原来唯一的终态f2作为最后构造出来的M的唯一的终态
• 保留M1,M2内部转换关系。
• 增加ε弧从f1射到q2
  

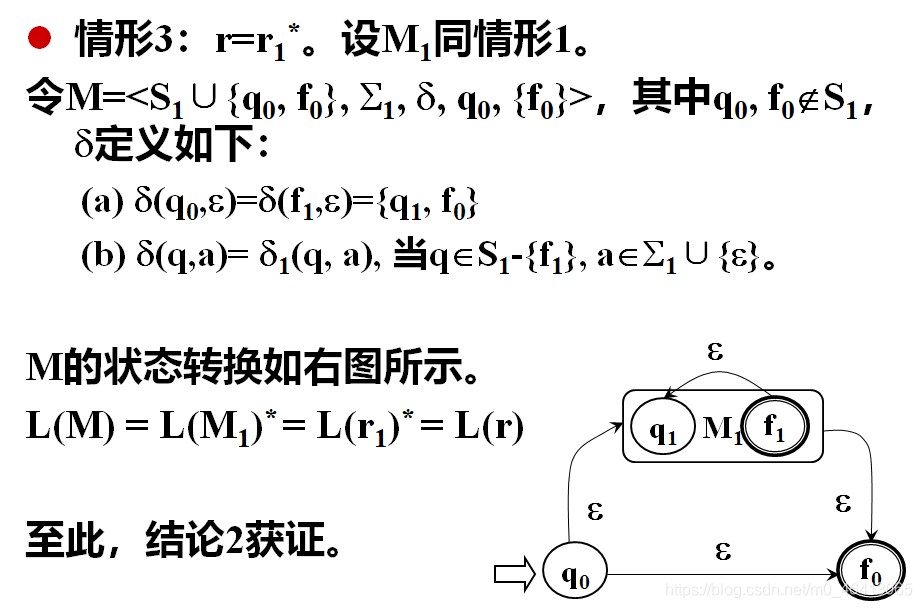
情形2 ： r=r1*

• 已知r1中间的运算符一定小于k，因为*（闭包）也算一个运算符。
• 故r1一定存在一个非确定有限自动机M1与之等价，并且L(M1)=L(r1)，且M1有唯一确定的初态q1和唯一确定的终态f1，并且终态没有射出弧
• 引入两个新状态，q0(唯一初态)和f0(唯一终态)
• 增加四个转换关系（4个ε弧），具体见下图
• 对M1之前的转换关系继续保留
  

上述过程展示了将正规表达式转化为非确定有限自动机的算法。

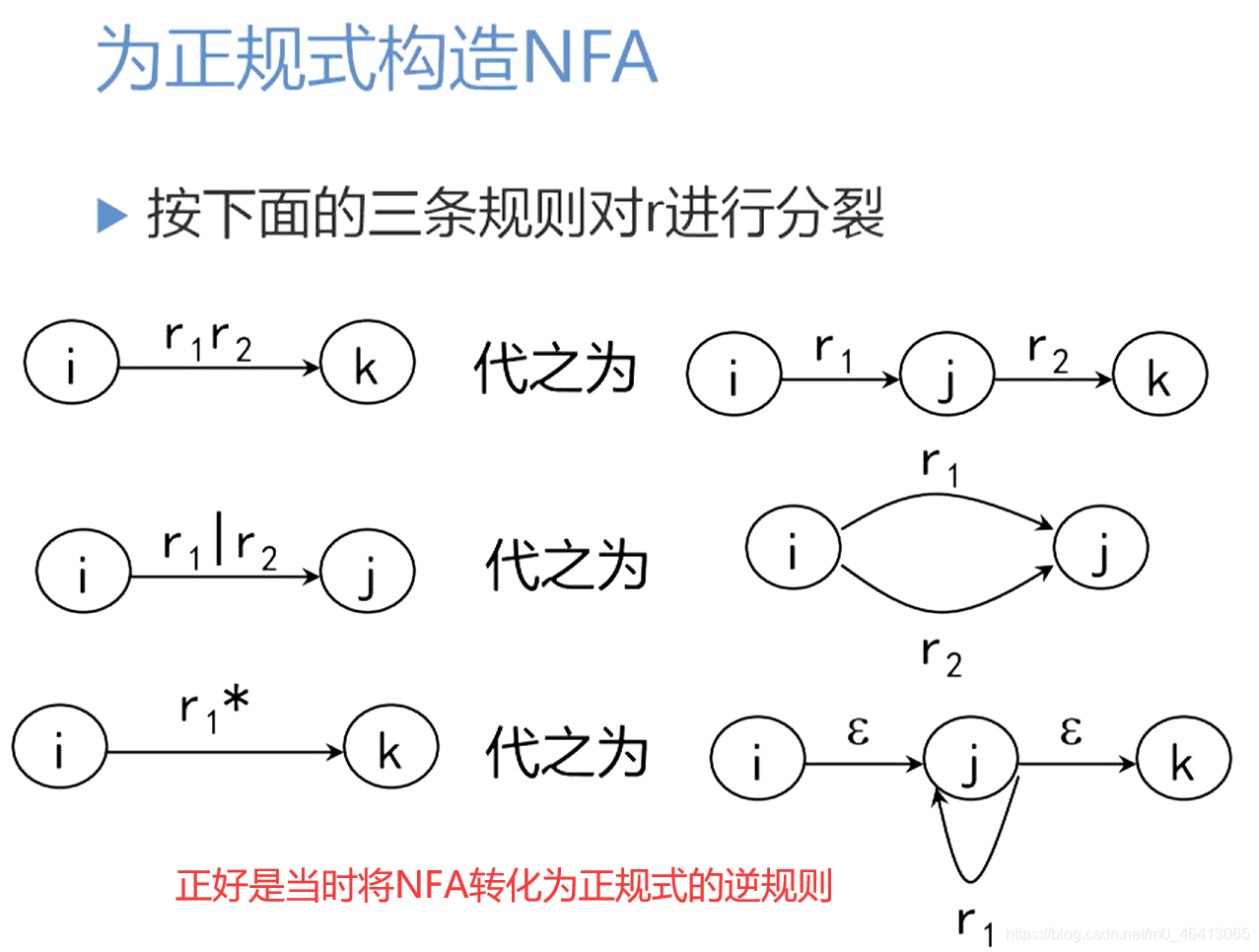
这三条规则的使用将使状态转换图上的节点和弧不断增多，但是弧上的标记越来越短
反复使用这些规则，就能逐步把这个图转变为每条弧只标记为工上的一个字符或ε，最后得到一个NFA M’，显然L(M’)=L®
这一过程和NFA确定化成DFA时所做的工作是类似的

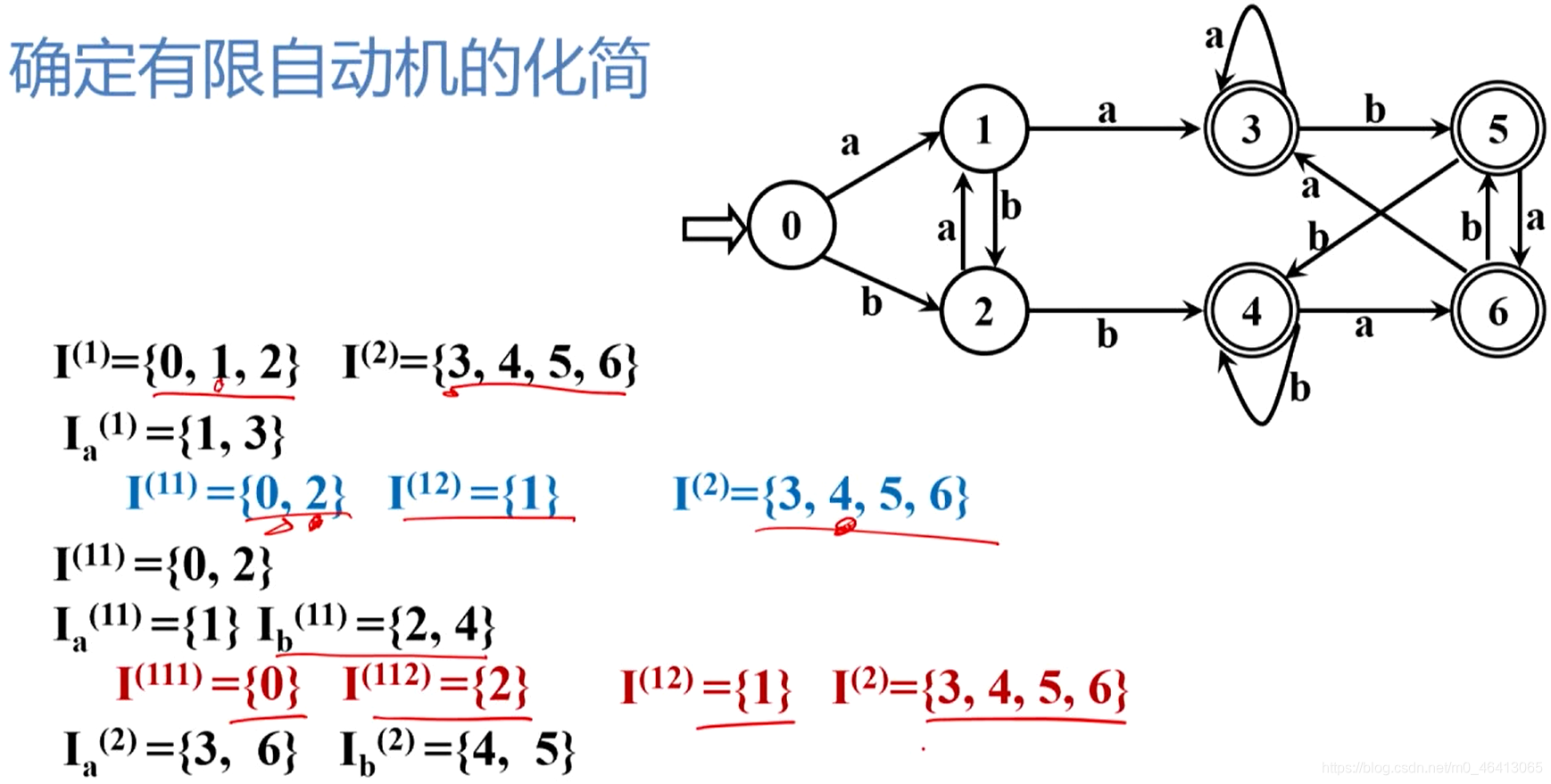
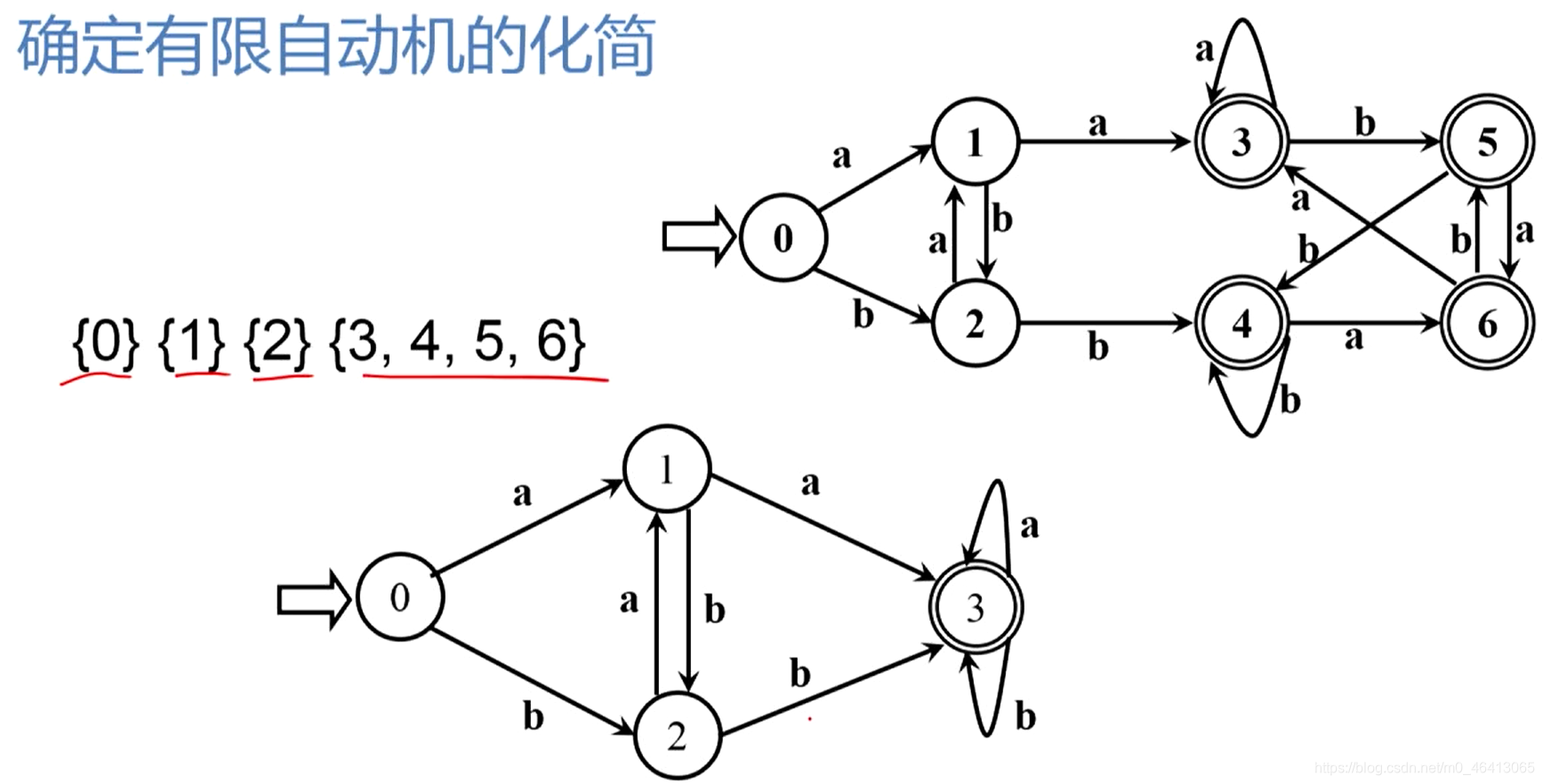
3.3.6 确定有限自动机DFA的化简

DFA的化简(最小化)

• 对于给定的DFA M，寻找一个状态数比M少的DFA M’，使得L(M)=L(M’)
  两个状态s和t等价的条件为：
• 一致性条件: 状态s和t必须同时为终态或非终态；
• 蔓延性条件: 对于所有输入符号，状态s和t必须转换到等价的状态里。

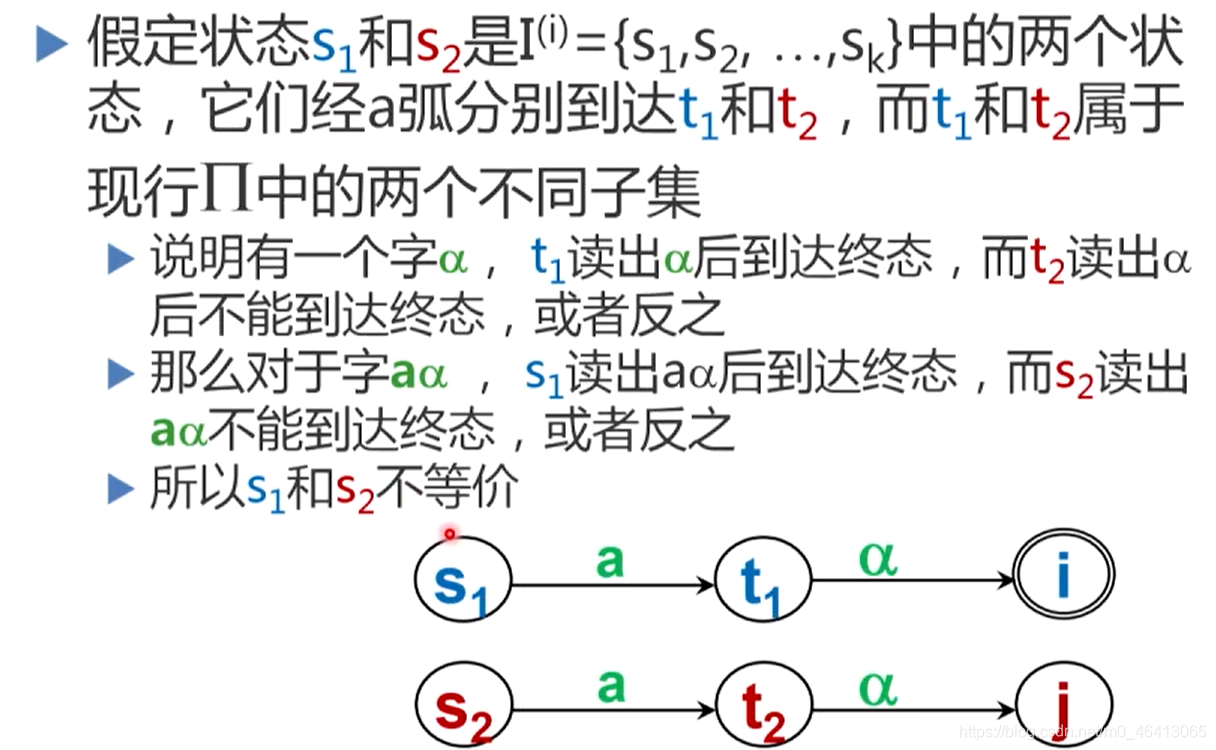
假设s和t为M的两个状态，称s和t等价∶如果从状态s出发能读出某个字α而停止于终态，那么同样，从t出发也能读出α而停止于终态;反之亦然。
p.s.两个终态可以不一样

• 两个状态不等价，则称它们是可区别的。

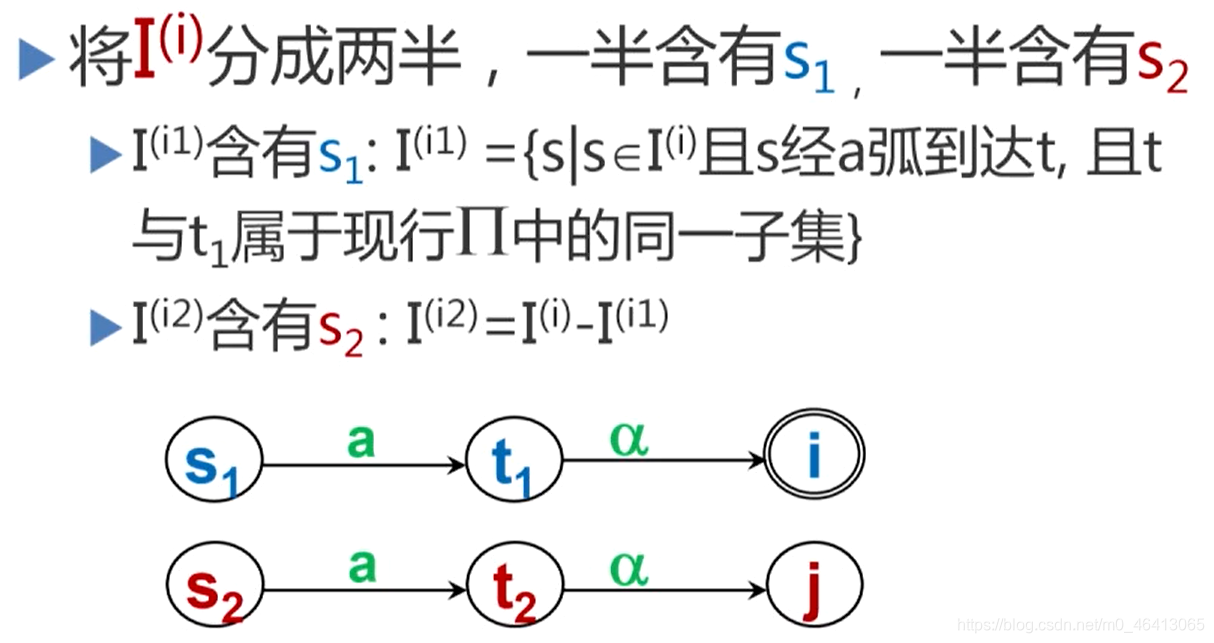
具体做法