【Practical】关于细分偏序格的一些补充_设由集合 a 上划分所组成的集合为 c,证明 c 上的“细分”关系是偏序关系

• 第一部分给出论域为 $n$ 元集合上的全部划分集合为载体，以细分关系为偏序关系的细分偏序格的高度问题；第二部分对划分的积运算、和运算进行补充与一些理解的记录。

细分偏序格高度.

• 关于一个 $n$ 元集合上的全部等价关系数量，组合数学中有结论如下：$n$ 元集合上全部等价关系的数量由对应的贝尔数 $B_n$ 给出。
• 由于等价关系、等价类以及划分三者是等价的，因此贝尔数 $B_n$ 实际上给出了 $n$ 元集合上全部划分的数量。
• 贝尔数由递推公式给出：$$B_0=B_1=1$$$$B_{n+1}=\sum _{k=0}^n\left(\genfrac{}{}{0ex}{}{n}{k}\right)B_k$$从而我们能够得到：$$B_2=\left(\genfrac{}{}{0ex}{}{1}{0}\right)B_0+\left(\genfrac{}{}{0ex}{}{1}{1}\right)B_1=2$$$$B_3=\left(\genfrac{}{}{0ex}{}{2}{0}\right)B_0+\left(\genfrac{}{}{0ex}{}{2}{1}\right)B_1+\left(\genfrac{}{}{0ex}{}{2}{2}\right)B_2=5$$$$\cdots \cdots$$
• 如果熟悉第二类Stirling数 $S(n,k)$ —— 把基数为 $n$ 的集划分为正好 $k$ 个非空集的方法的数目，那么我们很自然地可以对贝尔数 $B_n$ 进行分解：对于划分而言，我们对划分势从 $1$ 到 $n$ 求和，对应着原始集合整个作为等价类到每个元素成为一个等价类，所以得到：$$B_n=\sum _{k=1}^{n}S(n,k)$$
• 其中第二类Stirling数的计算式如下：$$S(n,k)=\frac{1}{k!}\sum _{i=0}^k(-1{)}^i(\genfrac{}{}{0ex}{}{k}{i})(k-i{)}^n$$
• 首几项的贝尔数为：$1,1,2,5,15,52,203,877,4140,21147,115975.$

---

• 关于 $n$ 元素集合对应细分偏序格的高度，其中划分势相同的划分会位于同一层，而划分势的取值从 $1$ 到 $n$，因此其高度为 $n.$ $n=4$ 时的例子如下图所示：
  

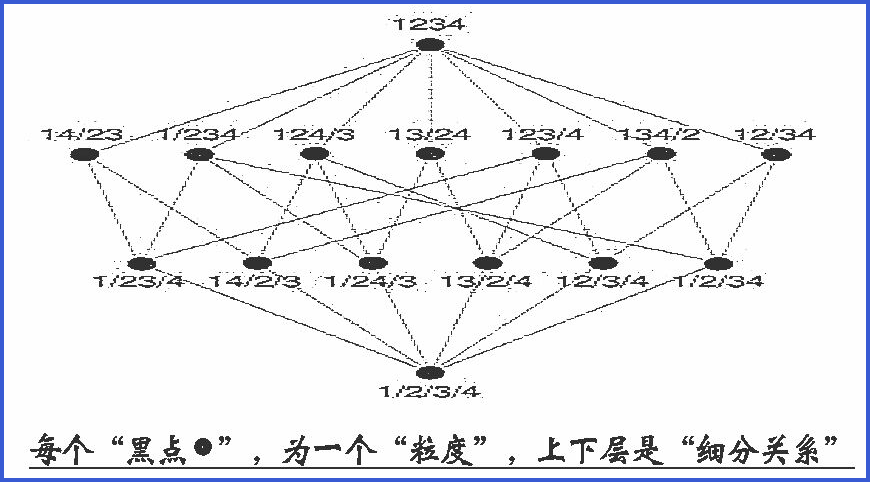
划分积与和.

• 【定义】两划分 ${\pi }_1,{\pi }_2$ 的积 ${\pi }_1\cdot {\pi }_2$ 是细分 ${\pi }_1,{\pi }_2$ 的最小划分。
• 【定义】两划分 ${\pi }_1,{\pi }_2$ 的和 ${\pi }_1+{\pi }_2$ 是被 ${\pi }_1,{\pi }_2$ 同时细分的最大划分。
  
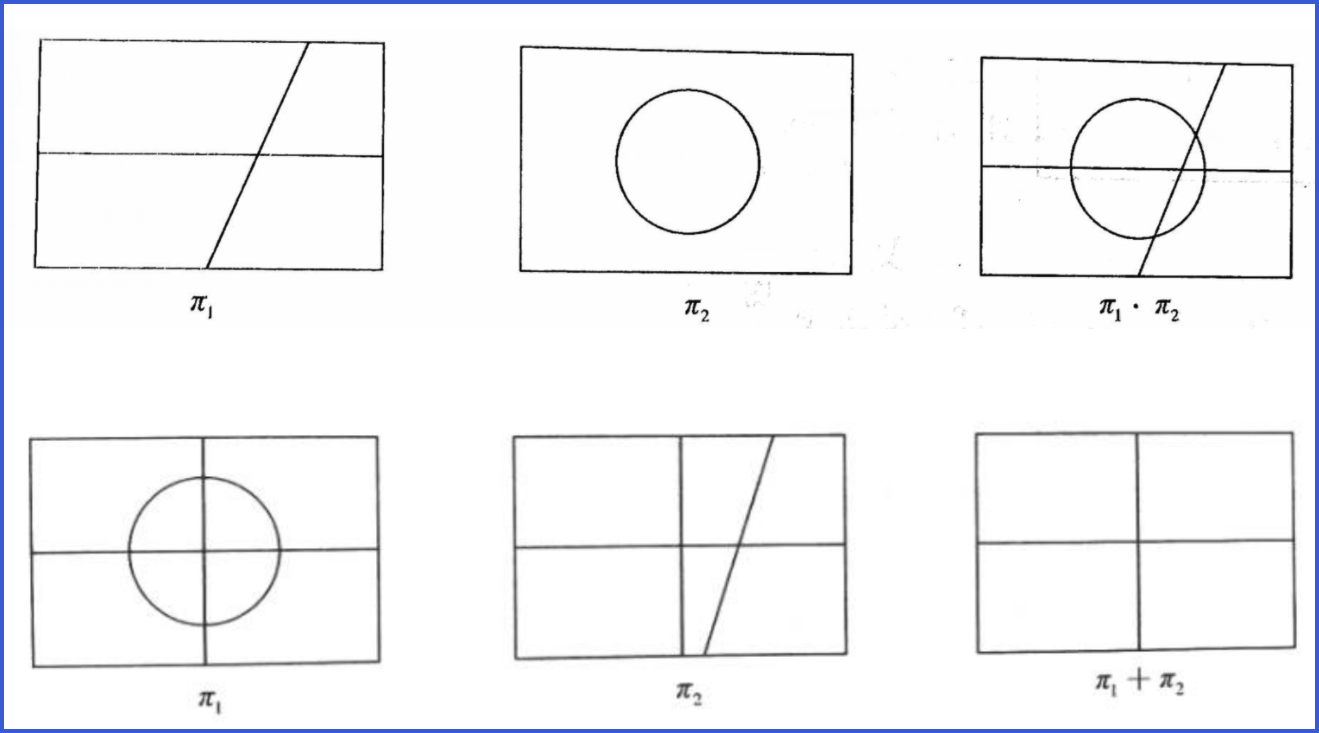
• 这里的大小以划分势来衡量，显而易见，上图中我们对 ${\pi }_1\cdot {\pi }_2$ 进一步细分得到的划分 ${\pi }^{\prime }$ 必然细分 ${\pi }_1,{\pi }_2$，但存在 $|{\pi }^{\prime }|>|{\pi }_1\cdot {\pi }_2|$；同样的，如果对 ${\pi }_1+{\pi }_2$ 减少划分的程度得到 ${\pi }^{\prime \prime }$( 一个极端是全集作为等价类 )，那么 ${\pi }_1,{\pi }_2$ 必然细分 ${\pi }^{\prime \prime }$，但存在 $|{\pi }^{\prime \prime }|<|{\pi }_1+{\pi }_2|.$
• 划分的积与和，从另一种角度也可以视为闭包closure、核kernel.

---

• 以集合 S = { 1 , 2 , 3 , 4 , 5 } S=\{1,2,3,4,5\} S={1,2,3,4,5} 为例，现指定划分 π 1 = { { 1 , 2 } , { 3 } , { 4 , 5 } } \pi_1=\Big\{\{1,2\},\{3\},\{4,5\}\Big\} π1​={{1,2},{3},{4,5}}， π 2 = { { 1 } , { 2 , 3 } , { 4 , 5 } } \pi_2=\Big\{\{1\},\{2,3\},\{4,5\}\Big\} π2​={{1},{2,3},{4,5}}，我们得到： π 1 ⋅ π 2 = { { 1 } , { 2 } , { 3 } , { 4 , 5 } } \pi_1\cdot\pi_2=\Big\{\{1\},\{2\},\{3\},\{4,5\}\Big\} π1​⋅π2​={{1},{2},{3},{4,5}} π 1 + π 2 = { { 1 , 2 , 3 } , { 4 , 5 } } \pi_1+\pi_2=\Big\{\{1,2,3\},\{4,5\}\Big\} π1​+π2​={{1,2,3},{4,5}}
• 从格代数的角度来看，划分的积与和分别对应着最大下界与最小上界运算，即：$${\pi }_1\cdot {\pi }_2=glb({\pi }_1,{\pi }_2)$$$${\pi }_1+{\pi }_2=lub({\pi }_1,{\pi }_2)$$

---